Принятие проектных решений в любой отрасли промышленности и оценка их качества в основном осуществляются на основании данных эксперимента.
Экспериментом называют целенаправленное воздействие на объект исследования с целью получения о нем достоверной информации.
Планирование эксперимента – это средство построения математических моделей различных процессов с целью повышения эффективности экспериментальных исследований: сокращения времени и средств на проведение эксперимента, повышения достоверности результатов исследования.
Основой теории планирования эксперимента является математическая статистика, так как результаты эксперимента могут рассматриваться как случайные величины или случайные процессы.
Эксперименты классифицируют по структуре на:
По стадии научных исследований различают:
По характеру постановки задачи для определения модели объекта эксперименты бывают:
По способу проведения различают:
Активный эксперимент позволяет быстро устанавливать закономерности, находить оптимальные режимы функционирования объекта, но его обычно и труднее осуществить. Вмешательство в технологический процесс может привести к снижению производительности и выпуску бракованной продукции. Иногда, например, при астрономических наблюдениях активный эксперимент вообще невозможен.
В общем виде объект исследования можно представить структурной схемой, приведенной на рисунке ниже.
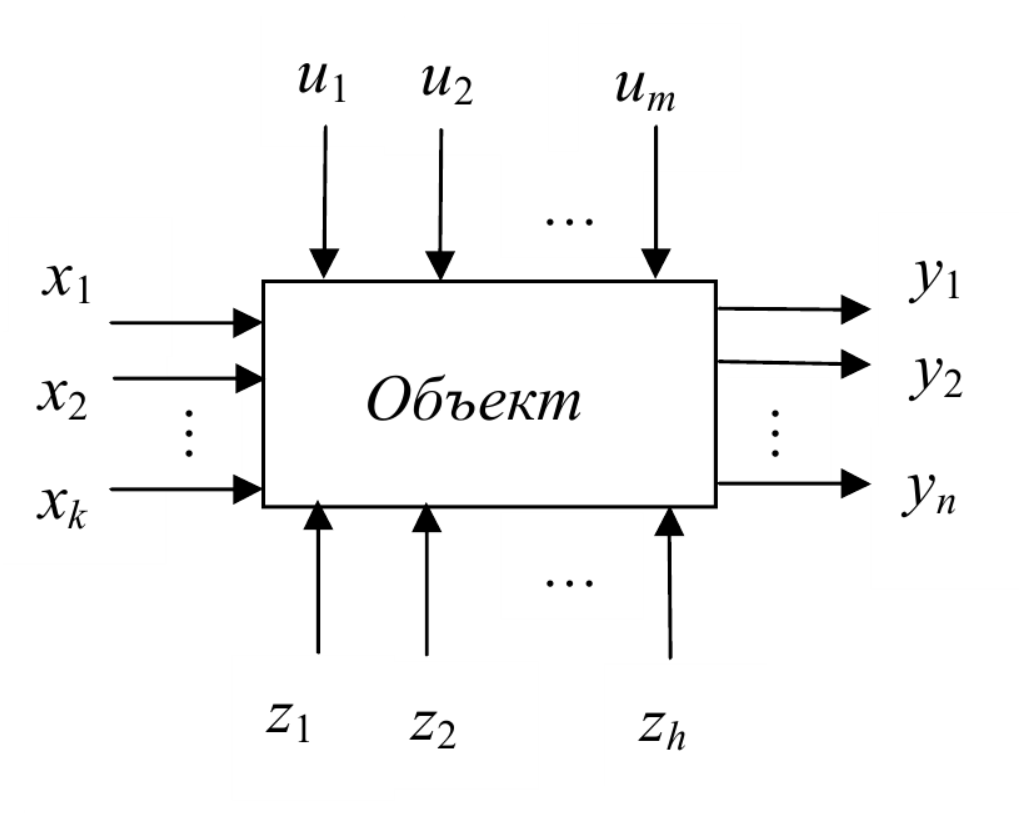
Состояние объекта исследования можно представить зависимостью
$$Y=f(X,U,Z),$$где $X=(x_1, x_2, ..., x_k)$ – независимые управляющие (входные) переменные, которые в процессе эксперимента можно целенаправленно изменять (питающее напряжение, технологические режимы и т. п.); $U=(u_1,u_2,...,u_m)$ – контролируемые возмущающие воздействия, которые не допускают целенаправленного изменения в ходе исследования (температура окружающей среды, освещение и т.п.); $Z=(z_1, z_2,..., z_h)$ – неконтролируемые и неуправляемые возмущения, неизвестные исследователю, медленно изменяющиеся во времени случайным образом; $Y=(y_1, y_2, ..., y_n)$ – контролируемые или вычисляемые параметры, характеризующие состояние объекта.
Такое представление объекта основано на широко используемом в технике принципе «черного ящика», т.е. системы, структура которой скрыта от наблюдателя, а суждение об ее функционировании создается только на основании внешних воздействий и ответствующих им реакциях системы. Следовательно, одной из основных задач эксперимента является выявление взаимосвязей между входными и выходными параметрами объекта и представление их в количественной форме в виде математической модели. Такая модель является математическим отображением наиболее существенных взаимосвязей между параметрами объекта. Она представляет собой совокупность уравнений, условий и алгоритмических правил и позволяет получить информацию о процессах, протекающих в объекте, которая может быть использована для управления моделируемым объектом с целью поиска оптимальных условий, а также анализировать и проектировать системы.
Входные параметры, которые оказывают влияние на объект и могут быть измерены, называют факторами. Так, например, при исследовании измерительного преобразователя с целью получения его математической модели в качестве факторов могут выступать измеряемая величина, температура окружающей среды, напряжение питания и т.п. Очевидно, что при планировании активного эксперимента факторы должны быть управляемыми и независимыми. Каждый фактор имеет область определения, которая должна быть установлена до проведения эксперимента.
В зависимости от источника информации, используемого при построении математической модели, различают физические (аналитические) и статистические (эмпирические) модели.
Физические модели представляют в виде сложных систем уравнений (алгебраических, дифференциальных, интегральных или дифференциально-интегральных), позволяющих очень точно описать процессы, протекающие в объекте, и допускающих экстраполяцию в точки факторного пространства, в которых невозможно непосредственное наблюдение этих процессов.
Статистические модели получают в результате статистической обработки экспериментальной информации, собранной об исследуемом объекте. Эти модели имеют относительно простую структуру и часто представляются в виде полиномов. Область их применения ограничивается ближайшей окрестностью рабочих точек, в которых проводятся эксперименты. Во многих случаях построение таких моделей можно выполнить при сравнительно небольших затратах времени и средств.
Принято также различать стационарные и динамические модели. Первые из них представляют неизменяющиеся во времени соотношения, вторые описывают переходные процессы, т.е. нестационарные состояния.
В общем случае планирование и организация эксперимента включают в себя следующие последовательно выполняемые этапы:
Можно выделить несколько типичных задач, решаемых экспериментатором. Это: