Физическая величина – это свойство, общее в качественном отношении для многих физических объектов, но индивидуальное для каждого из них в количественном отношении.
Качественная сторона понятия «физическая величина» определяет «род» величины (например, электрическое сопротивление как общее свойство проводников), а количественная – ее «размер» (сопротивление конкретного исследуемого проводника). Индивидуальность в количественном отношении понимают в том смысле, что свойство может быть для одного объекта в определенное число раз больше или меньше, чем для другого.
Выделяют измеряемые физические величины, которые могут быть выражены количественно в виде определенного числа установленных единиц измерения, и оцениваемые величины, для которых по каким-либо причинам не может быть введена единица измерения.
По видам явлений физические величины делятся на следующие группы:
Значение физической величины – оценка размера физической величины в виде некоторого числа принятых для нее единиц измерения.
Истинным значением физической величины называется значение физической величины, которое идеальным образом отражало бы в качественном и количественном отношении соответствующее свойство объекта. Определить экспериментально его невозможно вследствие неизбежных погрешностей измерения.
Действительным значением физической величины называется значение физической величины, найденное экспериментальным путем и настолько приближающееся к истинному значению, что для данной цели может быть использовано вместо него.
Единица физической величины – физическая величина фиксированного размера, которой, по определению, условно присвоено стандартное числовое значение, равное единице. Она применяется для количественного выражения однородных физических величин.
Единицы физических величин подразделяются на основные и производные и объединяются в соответствии с принятыми принципами в системы единиц физических величин.
Физические величины, встречающиеся в эксперименте, относят к следующим основным типам:
Измерением называется процесс нахождения значения физической величины опытным путем с помощью специальных технических средств.
Получаемая при измерениях физических величин информация называется измерительной. Зачастую информация об объекте измерения известна до проведения исследований. Такую информацию об объекте измерения называют априорной информацией. При полном отсутствии этой информации измерение в принципе невозможно, так как неизвестно, что же необходимо измерить, а следовательно, нельзя выбрать нужные средства измерений. При наличии априорной информации об объекте в полном объеме, т.е. при известном значении измеряемой величины, измерения попросту не нужны. Априорная информация определяет достижимую точность измерений и их эффективность.
Результат измерений физической величины – это значение физической величины, полученное путем ее измерения.
Принцип измерений – совокупность физических явлений, на которых основаны измерения.
Средство измерений – это техническое средство, предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящее и (или) хранящее единицу физической величины, размер которой принимается неизменным в течение известного интервала времени.
Метод измерений – совокупность приемов использования принципов и средств измерений.
Сходимость результатов измерений характеризует качество измерений, отражающее близость друг к другу результатов измерений одной и той же величины, выполняемых повторно одними и теми же методами и средствами измерений в одних и тех же условиях.
Воспроизводимость результатов измерений – характеристика качества измерений физической величины, отражающая близость друг к другу результатов измерений одной и той же величины, полученных в разных местах, разными методами и средствами измерений, разными операторами, но приведенных к одним и тем же условиям.
Методы измерений определяются физическим характером измеряемой величины, требуемой точностью измерений, необходимой скоростью измерения, условиями и пр. Наибольшее распространение получила классификация по общим приемам получения результатов измерений. Согласно этому признаку, измерения делятся на прямые, косвенные, совместные и совокупные.
Наиболее часто применяются прямые измерения, состоящие в том, что искомое значение величины находят из опытных данных путем экспериментального сравнения. Математически прямые измерения можно охарактеризовать элементарной формулой $A=x$. Часто под прямыми понимаются такие измерения, при которых не производится промежуточных преобразований.
Если искомое значение величины находят на основании известной закономерности между этой величиной и величинами, найденными прямыми измерениями, то этот метод измерений называют косвенным. Уравнение косвенного измерения $A = f(x_1, x_2,..., x_n)$, где $x_i$ – результат $i$-го прямого измерения.
Совокупные измерения осуществляются путем одновременного измерения нескольких одноименных величин, искомое значение при этом находят решением системы уравнений, получаемых в результате прямых измерений различных сочетаний этих величин. При этом могут измеряться несколько комбинаций значений величин.
Совместными называют одновременно проводимые измерения двух и более неодноименных величин с целью нахождения функциональной связи между этими величинами.
Косвенные, совместные и совокупные измерения объединяются одним принципиально важным общим свойством: их результаты рассчитываются по известным функциональным зависимостям между измеряемыми величинами и величинами, определенными путем прямых измерений.
Погрешностью измерения называется отклонение результата измерения от истинного значения измеряемой величины. Т.к. истинное значение измеряемой величины неизвестно, то при количественной оценке погрешности пользуются действительным значением физической величины.
Погрешность результата измерения можно оценить с разной точностью на основании различной исходной информации. В соответствии с этим различают измерения с точной, приближенной и предварительной оценкой погрешностей. При измерениях с точной оценкой погрешности учитывают индивидуальные метрологические свойства и характеристики каждого из примененных средств измерений, анализируют метод измерений, контролируют условия измерений с целью учета их влияния на результат измерения. Если измерения ведут с приближенной оценкой погрешности, то учитывают лишь метрологические характеристики средства измерений и оценивают влияние на результат только отклонения условий измерения от нормальных. Измерения с предварительной оценкой погрешности выполняются по типовым методикам, регламентированным нормативными документами, в которых указаны методы и условия измерений, типы погрешностей и т.д., и на основе этих данных заранее оценена возможная погрешность результата.
По форме количественного выражения погрешности измерения разделяются на абсолютные, относительные и приведенные.
Абсолютной погрешностью, выражаемой в единицах измеряемой величины, называется отклонение результата измерения от истинного значения
$$\Delta = Y(x)-x.$$Абсолютная погрешность характеризует величину и знак полученной погрешности, но не определяет качество самого измерения.
Чтобы иметь возможность сравнивать качество измерений, используют относительную погрешность. Относительной погрешностью называется отношение абсолютной погрешности результата измерения к истинному значению измеряемой величины
$$\delta = \frac{\Delta}{x}.$$Мерой точности измерений служит показатель, обратный модулю относительной погрешности
$$t_T=\frac{1}{|\delta|}$$Приведенной погрешностью, выражающей потенциальную точность измерений, называется отношение абсолютной погрешности к некоторому нормирующему значению (например, конечное значение шкалы прибора, предел измерений)
$$\gamma=\frac{\Delta}{x_N}·100%.$$По характеру проявления погрешности измерений подразделяются на три основных класса: систематические, случайные и грубые (промахи).
Систематические погрешности – составляющие погрешности измерений, остающиеся постоянными или закономерно изменяющиеся при многократных измерениях одной и той же величины в одних и тех же условиях.
Случайные погрешности – составляющие погрешности измерений, изменяющиеся случайным образом по значению и по знаку при повторных измерениях одной и той же физической величины в одних и тех же условиях. Практически случайные погрешности неизбежны, неустранимы и всегда имеют место в результате измерения. Однако их можно уменьшить путем многократного измерения физической величины и последующей статистической обработкой полученных результатов.
Грубые погрешности (промахи) – погрешности, существенно превышающие ожидаемые при данных условиях измерения. Грубые погрешности возникают из-за ошибок оператора или неучтенных внешних воздействий. В случае однократного измерения промах обнаружить нельзя. При многократных измерениях промахи выявляют в процессе обработки результатов и исключают из рассмотрения, пользуясь определенными правилами.
Таким образом, если не учитывать промахи, абсолютная погрешность измерения имеет систематическую и случайную составляющие:
$$\Delta=\Delta_{сист} + \Delta_{случ}$$По причинам возникновения погрешности измерения подразделяются на методические, инструментальные, внешние и субъективные (личные).
Методические погрешности возникают из-за несовершенства метода измерений, некорректности алгоритмов или формул, по которым производятся вычисления результатов измерений, отличия принятой модели объекта измерения от той, которая правильно описывает его свойство, определяемое путем измерения, а также из-за влияния выбранного средства измерений на измеряемые параметры сигналов.
Инструментальные (приборные) погрешности возникают из-за несовершенства средств измерений. Источниками инструментальных погрешностей могут быть, например, неточная градуировка прибора и смещение нуля, вариации показаний прибора в процессе эксплуатации.
Внешняя погрешность – составляющая погрешности измерения, связанная с отклонением одной или нескольких влияющих величин от нормальных значений или выходом за пределы нормальной области (влажность, температура, нестабильность источников питания).
Субъективные погрешности вызываются ошибками оператора при отсчете показаний средств измерения.
По характеру поведения измеряемой величины в процессе измерений различают статические и динамические погрешности.
Статические погрешности возникают при измерении установившегося значения измеряемой физической величины.
Динамические погрешности имеют место при динамических измерениях, когда измеряемая величина изменяется во времени и требуется установить закон ее изменения. Причина появления динамических погрешностей состоит в несоответствии скоростных (временных) характеристик прибора и скорости изменения измеряемой величины.
По условиям эксплуатации средств измерений различают основную и дополнительную погрешности.
Основная погрешность средства измерений имеет место при нормальных условиях эксплуатации, оговоренных в регламентирую щих документах.
Дополнительная погрешность возникает вследствие выхода какой-либо из влияющих величин за пределы нормальной области значений.
Результат измерения представляет собой случайную величину следующей структуры:
$$Y=k·x + k·F + H,$$где $k·x$ – мультипликативная составляющая результата измерения ($k$ – коэффициент чувствительности средства измерений СИ); $k·F$ – аддитивная случайная составляющая результата измерения, обусловленная возмущением, действующим на измеряемую величину $x$ на входе средства измерений; $H$ – аддитивная составляющая, обусловленная возмущением, действующим на измеряемую величину $x$ на выходе средства измерений [округление (квантование) результата измерения, субъективные ошибки оператора, выполняющего измерение].
Формирование результата измерения можно изобразить в виде структурной схемы.
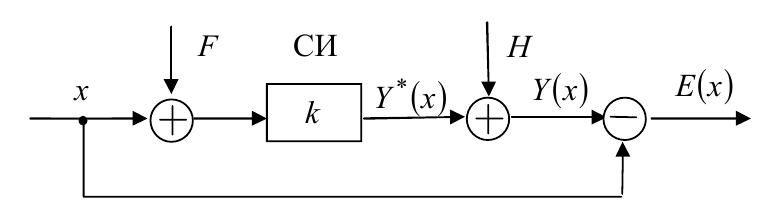
Погрешность результата измерения равна
$$E(x) = Y(x) - x = k·x + k·F + H - x = (k -1)·x + k·F + H,$$где $(k -1)·x$ – мультипликативная составляющая погрешности; $k·F$ – аддитивная случайная составляющая, обусловленная случайным возмущением, действующим на входе средства измерений; $H$ – аддитивная составляющая, обусловленная случайным возмущением, действующим на выходе средства измерений.
Главная особенность мультипликативной погрешности состоит в том, что она зависит от значения измеряемой величины. Причина ее появления состоит в том, что размер единицы величины, воспроизводимой средством измерений, не равен единице. Особенности аддитивных составляющих погрешности состоят в том, что они не зависят от измеряемой величины. Причинами их появления являются аддитивные возмущения, действующие на входе и выходе средства измерений. Они всецело определяются аддитивными составляющими результата измерения.