Как и большинство слов, термин «управление» является многозначным, употребляется в разных смыслах. Исходным является определение управления как целенаправленного воздействия на систему. Это перефразировка понятия «преобразовательная деятельность» - субъект старается изменить реальность, приблизить ее состояние к желаемому.
Первым компонентом управления является сам объект управления, управляемая система. Обозначим выходы некоторой системы $S$ символом $Y(t)$, а входы ее разделим на управляемые извне $U(t)$ и неуправляемые, но наблюдаемые $V(t)$. Мы знаем, что есть входы и ненаблюдаемые, неизвестные нам, но неизвестное невозможно включить в модель иначе, как через понятие стохастичности: наблюдаемые величины оказываются случайными. И даже при этом остается то неизвестное, что не отображено случайностью известного.
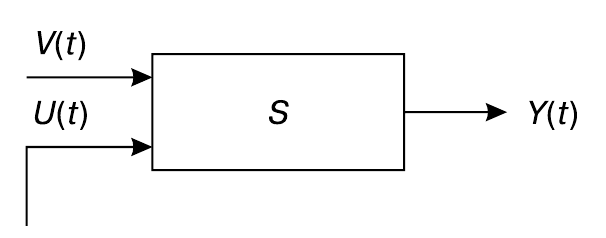
Само выделение управляемых входов означает, что мы рассматриваем систему $S$ как объект управления. Выходы $Y(t)$ являются результатом преобразования системой $S$ входов $V(t)$ и $U(t): Y(t) = S(V(t),U(t))$, что позволяет воздействовать на $Y(t)$ путем выбора различных управлений $U(t)$ (заметим, что приведенная символика верна только для безынерционных систем, хотя в реальности выход системы зависит не только от входов в данный момент времени, но и от их предыстории.).
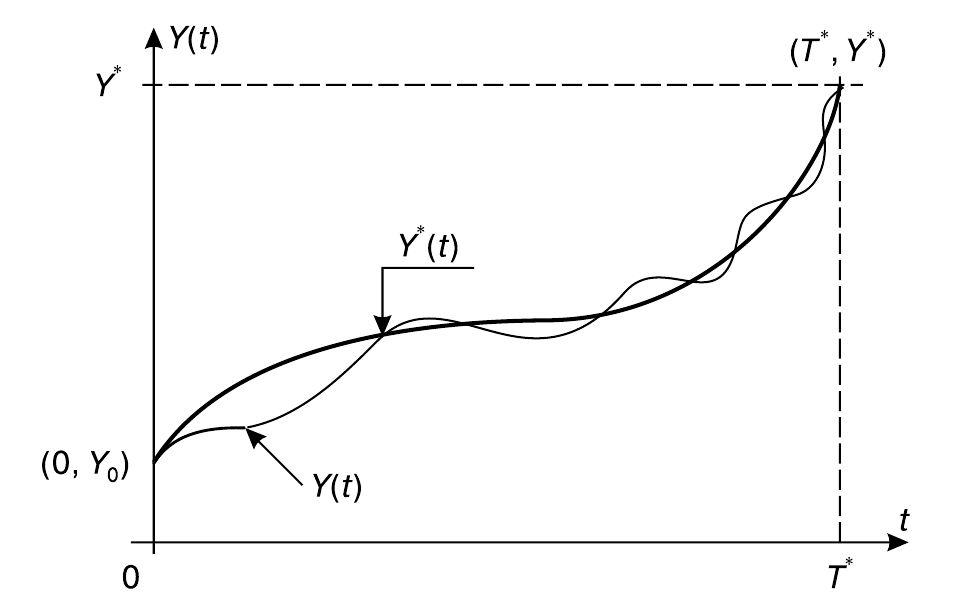
Вторым обязательным компонентом системы управления является цель управления. Напомним, что в понятие цели входит не только конечное желаемое состояние системы $(T^*,Y^*)$, но и весь желаемый путь к ней $Y^*(t)$. Напомним также, что как бы мы ни старались учесть все ограничения при формулировке цели, она остается субъективной: во-первых, мы учли только то, что нам известно, а наши знания всегда ограниченны; во-вторых, как именно и насколько правильно мы это сделали — итог нашей работы, неизбежно несущей отпечаток личности. Так что вопрос о фактической достижимости поставленной цели с помощью системы $S$ остается открытым до начала самого процесса управления.
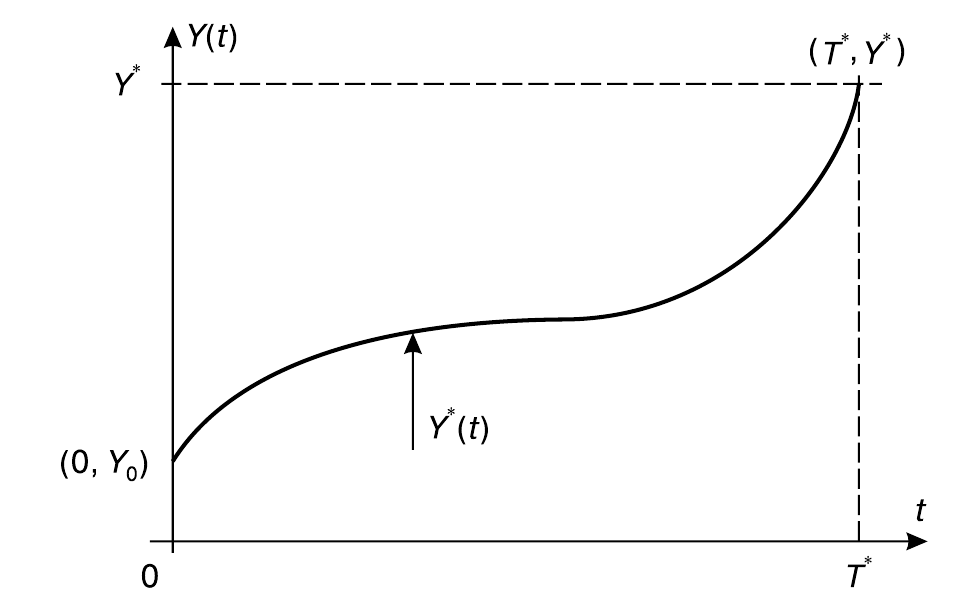
Управляющее воздействие $U(t)$ есть третий компонент управления. Тот факт, что входы и выходы системы связаны между собой некоторым соотношением $Y(t)=S[V(t), U(t)]$, позволяет надеяться на то, что существует такое управляющее воздействие $U^*(t)$, при котором на выходе реализуется цель $Y^*(t)$:
$$Y^*(t)=S[V(t), U^*(t)].$$Но как узнать, действительно ли оно существует, и если да, то каково оно? Для этого нужно решить уравнение относительно $U^*(t)$. В этом уравнении известны $Y^*(t)$ (задано) и $V(t)$ (наблюдаемо), но оператор $S$ обычно неизвестен, что делает задачу неразрешимой. Выход все равно надо искать, и это приводит к двум типам управления.
Первый состоит в том, чтобы подать на управляемый вход какое-либо воздействие $U_i(t)$ и посмотреть, что получится. Если на выходе получится цель $Y^*(t)$ — нам крупно повезло. Если нет — подать какое-то другое воздействие $U_j(t)$ и пронаблюдать результат. И действовать так и дальше до достижения нужного результата, т.е. искать нужное воздействие $U^*(t)$ путем перебора воздействий на самой системе $S$. Иногда такой способ оказывается единственно возможным (например, поиск выхода из лабиринта), но чаще такой способ управления является неразумным по ряду причин. Например, множество возможных $U(t)$ может быть настолько большим (и даже бесконечным), что надеяться на случайное удачное попадание нереально. Другая важная причина — высокие потери при неверном решении. Например, $S$ — школа, $U(t)$ — методика обучения, $Y(t)$ — выпускники школы. Ясно, что метод перебора тут неуместен. Поэтому поиск нужного управляющего воздействия на самом управляемом объекте часто является неразумным, неприемлемым.
Второй подход основан на использовании всей имеющейся информации об управляемом объекте. Это означает, что поиск нужного управления следует осуществлять не на самой системе, а на ее модели. Таким образом, модель системы управляемоего объекта становится четвертой составляющей частью процесса управления. Вместо решения уравнения мы теперь должны решить относительно управляющего воздействия $Um^*(t)$ уравнение
$$Y^*(t) = S_m[V(t), U_m^*(t)],$$в котором известны $Y^*(t)$, $V(t)$ и $S_m$ — модель системы. В принципе (оставим в стороне технические трудности) такое уравнение может быть решено. Это и будет рациональным, разумным управлением.
Конечно, поиск управления на модели тоже требует потерь (расходы на процесс моделирования), но эти потери несравнимо меньше тех, которые мы понесли бы, ища нужное управление на самой системе.
Все действия, необходимые для управления, должны быть выполнены. Данная функция возлагается обычно на специально создаваемую для этого систему (пятую составляющую часть процесса управления), называемую блоком управления или системой (подсистемой) управления, управляющим устройством (регулятором) и т.п. В реальности блок управления может быть подсистемой управляемой системы (как заводоуправление — часть завода, автопилот — часть самолета), но может быть и внешней системой (как министерство для подведомственного предприятия, как аэродромный диспетчер для идущего на посадку самолета).

Попутным, но очень важным результатом является то, что мы установили два первых обязательных шага процесса управления:
Как использовать модель $S_m$ для поиска наилучшего управляющего воздействия? Употребив оценочное слово «наилучший», мы должны точно указать, в каком смысле употребляется эта оценка, т.е. задать критерий качества. Ясно, что управление тем «лучше», чем «ближе» выход системы $Y(t)$ к цели $Y^*(t)$. Но искать это управление мы будем на модели, поэтому на этапе поиска управления нам придется считать наилучшим то управление $U_m^*(t)$, которое максиимально приблизит к $Y^*(t)$ выход модели $Y_m(t)$.
Если выходы $Y_m(t)$ измеримы численно, то вводится некоторый числовой критерий («расстояние» между двумя функциями) $r = r(Y^*(t), Y_m(t))$, который равнялся бы нулю при совпадении сравниваемых функций и возрастал при любом их различии. Таких «расстояний» можно ввести много и по-разному. Например:
$$r_1 = \max|Y_m(t)-Y^*(t)|.$$ $$r_2 = \int_{t_1}^{t_2}\left(Y_m(t)-Y^*(t)\right)^2\mathrm{d}t.$$Выбрав некоторую меру различия двух функций, нам остается решить задачу на отыскание такого $U_m^*(t)$, которое доставляет функционалу $r$ минимум (лучше — ноль):
$$U_m^*(t) = \arg\left(\min_{U(t)}\left(r\left(Y^*(t),Y_m(V(t), U(t))\right)\right)\right).$$Для целей, задаваемых нечисловым способом, все равно вводятся измеримые характеристики близости результата к цели.
После подачи на управляемый вход системы найденного воздействия $U_m^*(t)$ система выдаст некоторый выходной процесс $Y(t)$:
$$Y(t) = S[V(t), U_m^*(t)],$$являющийся преобразованием входов оператором системы $S$. При этом возможны различные исходы, требующие различных действий по управлению системой. Это и порождает различные типы управления.
Первый тип управления — управление простой системой, или программное управление. Начнем с самого желательного случая — когда подача на вход системы $S$ воздействия $U_m^*(t)$, обеспечивающего цель $Y^*(t)$ на выходе модели $S_m$, приводит к такому же результату и на выходе управляемой системы $S$. Это означает, что наша модель $S_m$ оказалась адекватной, так как система $S$ послушно отработала заданную цель. В этом случае систему $S$ будем называть простой. Простота системы есть следствие адекватности модели. Управляющее воздействие $U_m^*(t)$ в этом случае называется программой, а данный тип управления — программным управлением.
Такой наиболее благоприятный случай иногда удается реализовать в практике. Примерами могут служить исправные бытовые приборы, различные автоматы и т.п.
Второй тип управления — управление сложной системой. Рассмотрим другой крайний случай — когда на найденное на модели управляющее воздействие $U_m^*(t)$ система откликается вовсе на так, как модель, $Y(t)$ не совпадает с $Y^*(t)$. Обозначим эту ситуацию соответствующей терминологией.
Начнем с констатации факта, что имеющаяся у нас модель не позволила достичь цели; наша модель $S_m$ неадекватна. Система $S$ ведет себя неожиданным для нас образом, не подчиняется нашему управлению («эта чертова штука ведет себя не так, как ей положено!»). Будем называть такую систему сложной. Причиной сложности системы при таком подходе оказывается неадекватность ее модели $S_m$.
Подчеркнем, что мы ввели специальное определение сложности. Есть много других определений; некоторые из них связывают понятие сложности с многокомпонентностью, разнокачественностью компонент; многомерностью компонентов управления и т.д. Мы будем употреблять термин «сложный» только в смысле недостаточности информации об управляемом объекте. С этой точки зрения сложность — это не свойство системы, а свойство тех, кто смотрит на систему.
Очевидно, что управление сложной системой сводится к добыванию недостающей информации о системе и последующему использованию этой информации для очередного акта управления. Это означает, что мы должны совершенствовать модель системы, повышать ее адекватность.
Будем исходить из предположения, что при построении модели $S_m$ мы использовали всю доступную информацию о системе — из учебников, монографий, справочников, Интернета, от экспертов. Тогда единственным источником информации остается только сама система и единственным способом извлечения этой информации является эксперимент с системой.
Эксперимент — это вопрос к системе, на который она дает честный ответ. Один вопрос мы уже задали. Подавая на управляемый вход воздействие $U_m^*(t)$, мы как бы спросили систему: «Дорогая, на это воздействие ты выдашь на выходе $Y^*(t)$?» А она ответила: «Нет, я не такая! Я откликаюсь функцией $Y(t)$». Эту полученную информацию надо включить в модель путем передачи информации по цепи обратной связи , и изменения, коррекции модели так, чтобы она на $U_m^*(t)$ откликалась той же функцией $Y(t)$, что и система. Теперь модель $S_m$ стала более похожей на систему $S$, по крайней мере на данном примере.
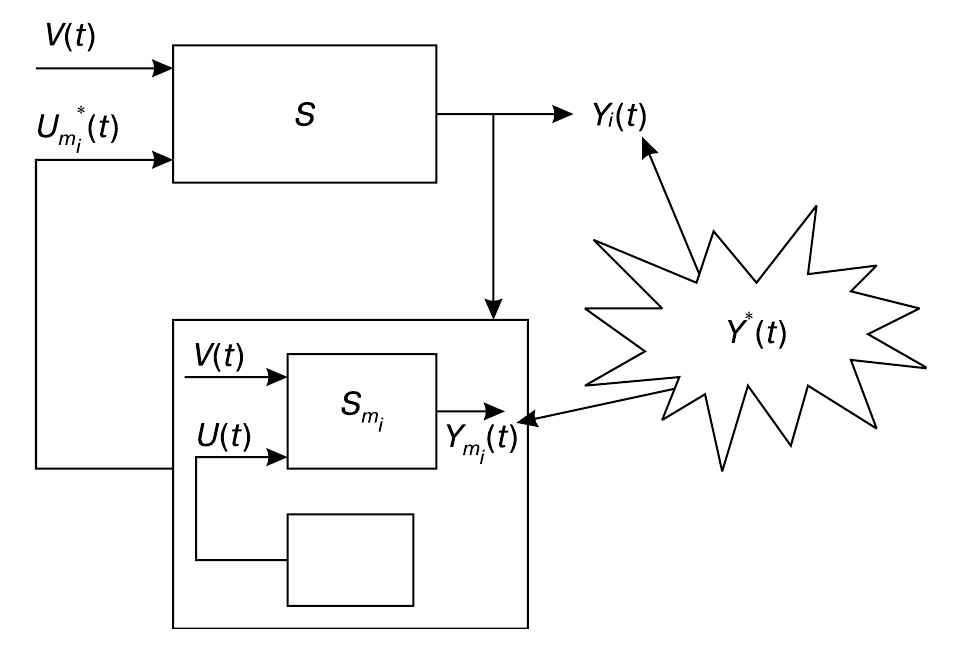
Новую, исправленную и дополненную модель $S_{mi}$ мы используем для поиска на ней следующего управляющего воздействия (поэтому на схеме введена индексация $i$ очередного шага $i = 1, 2, …$), $U_{mi}^*(t)$. И такие шаги повторяются, постепенно улучшая модель, повышая ее адекватность.
Итак, алгоритм управления сложной системой таков.
Еще раз обсудим особенности алгоритма управления сложной системой.
Во-первых, алгоритм имеет циклический, повторяющийся характер. С каждым циклом $S_{mi}$ улучшается, становится более адекватной, что повышает эффективность управления, уменьшает сложность системы. В некоторых случаях удается сложную систему превратить в простую за конечное число шагов. Примером является случай, когда вы забыли шифр, набранный вами у автоматической камеры хранения. Улучшение модели состоит в замене ее строки «на № X возможно откроется» после неудачной пробы № X на строку «на № X не откроется» и в соответствующем сокращении числа оставшихся вариантов.
В других случаях коррекция модели производится изменением ее параметров. Например, если модель — уравнение, меняются его коэффициенты, показатели, добавляются или устраняются члены уравнения и т.д. Если модель — физическое устройство, изменяются его установки, регулировки, переключения и т.д. Иногда эти действия приводят к достаточной адекватности модели, т.е. к упрощению системы. Но есть системы, сложность которых человечеству не удается исчерпать, несмотря на все старания (природа, общество, экономика, мышление и т.д.). Их иногда называют очень сложными системами.
Во-вторых, поскольку на каждом шаге будет получаться «не совсем цель $Y^*(t)$», мы при этом понесем потери. Такова цена незнания. Нам остается только минимизировать неизбежные потери при управлении сложной системой. Сделать это можно, лишь полностью, без потерь используя полученную в очередном эксперименте (шаге управления) информацию, т.е. сделать так, чтобы скорректированная модель как можно точнее имитировала поведение системы на каждом из предыдущих шагов.
Теперь пора привести широко употребляемое название этого метода, хотя и с некоторой неохотой из-за его лингвистических особенностей. В ходе формирования профессиональной терминологии для нужд теории и практики управления каждое очередное управляющее воздействие стали именовать пробным воздействием или просто пробой, а расхождение между $Y_i(t)$ и $Y^*(t)$ — ошибкой. Сам алгоритм управления сложной системой получил название метода проб и ошибок. Из-за этого названия некоторые путают его с «методом тыка». Кардинальное различие между ними заключается в том, что нужное воздействие ищется не на самой системе (это и есть «метод тыка»), а на модели системы, корректируемой по ходу управления. Можно сказать, что «метод тыка» — самый плохой метод управления сложной системой, а «метод проб и ошибок» — самый лучший. Хотя и при нем потери неизбежны — за невежество приходится расплачиваться.
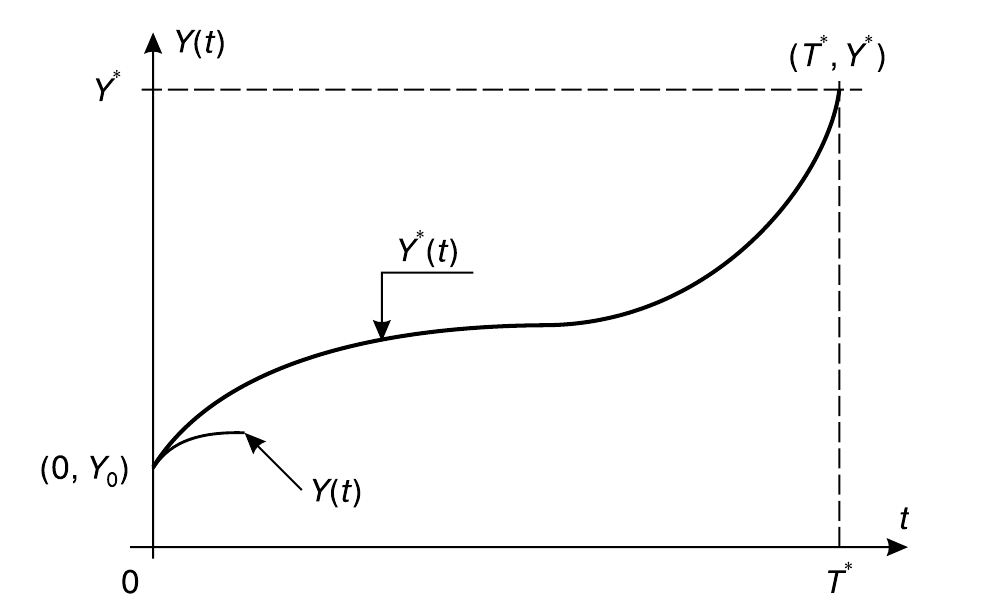
Третий тип управления — управление по параметрам, или регулирование. Рассмотрим теперь случай, промежуточный между первыми двумя. Подав $U_m^*(t)$, мы можем наблюдать, что поначалу система идет по желаемой траектории $Y^*(t)$, но через некоторое время обнаруживается расхождение между $Y(t)$ и $Y^*(t)$. Конечно, это значит, что модель не совсем точна. Но часто оказывается, что внесение поправок в модель нецелесообразно. Например, самолет, ведомый автопилотом, сбивается с курса порывом ветра. Вносить в модель этот порыв нет смысла. Но есть возможность внести изменения в саму систему. Первая возможность — изменение параметров системы, не изменяя ее структуры. Параметр изменяется так, чтобы система вернулась на целевую траекторию, и при дальнейших отклонениях $Y(t)$ от $Y^*(t)$ это действие повторяется.
Для реализации этого типа управления нужно выполнять следующие функции:
Для выполнения этих функций необходимо создать специальное устройство, дополнительную систему. Это устройство получило название регулятора, а сам метод управления — регулирования. Схема управления теперь выглядит по-другому.
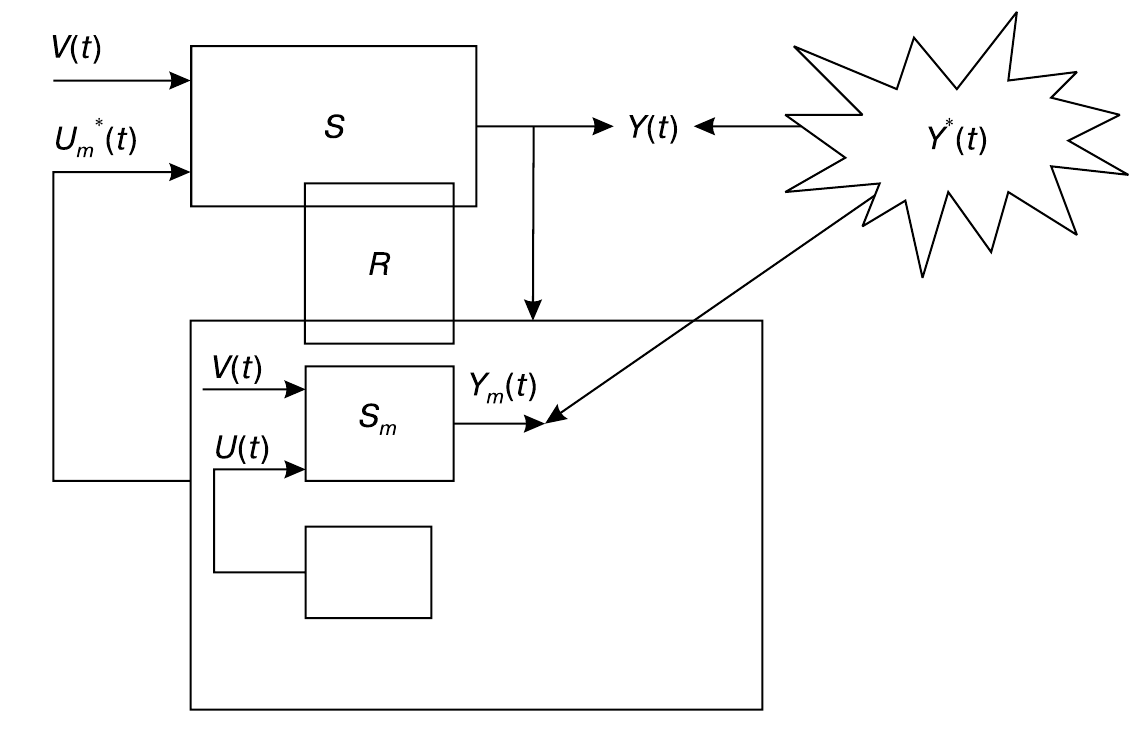
Регулятор изображен квадратиком «R». Он помещен на схеме в позицию, которая позволяет отнести его либо к самой управляемой системе, либо к системе управляющей, либо считать самостоятельной системой. Важно исполнение указанных функций, а где они физически будут исполняться, зависит от обстоятельств. Например, регулирующее управление самолетом может выполняться автопилотом, летчиком или аэродромным диспетчером.
Если программное управление называют управлением без обратной связи, то регулирование — управлением с обратной отрицательной связью (подчеркивая стремление уменьшить отклонение от опорной траектории; при положительной обратной связи отклонение стремятся увеличить, как, например, в автогенераторах).
Для осуществления регулирования необходимо, чтобы система отклонялась от опорной траектории не слишком быстро и не слишком далеко — так, чтобы за счет изменения параметров можно было бы ее возвратить на целевую траекторию $Y^*(t)$. В математической теории регулирования это условие называется «малостью» отклонений.
К сожалению, это условие иногда не выполняется. Например, автомобиль может выехать на обледеневший участок дороги, и никакие манипуляции с рулем и тормозами не смогут удержать его на дороге. Мы оказываемся в условиях, когда требуется другой тип управления.
Четвертый тип управления — управление по структуре. Когда система так быстро и так далеко отклоняется от целевой траектории, что не может быть возвращена на нее изменением параметров, перед нами два выхода: пессимистический и оптимистический. Пессимистический означает смирение перед невозможностью достичь конечную цель, иногда — гибель. Оптимистический связан с признанием фактов и предпринятием попытки все-таки достичь $(T^*,Y^*)$. Фактом является то, что эта цель недостижима для существующей системы. Но, может быть, она достижима для другой системы?
Изменим в момент $T_s$ структуру системы, создавая тем самым новую систему, с надеждой прибыть в точку $(T^*,Y^*)$ хотя бы и по другой траектории $Y_s^*(t)$. Такое управление и называется управлением по структуре. Можно различать случаи, когда новая структура создается только из частей (возможно, не всех) старой системы, и случаи вовлечения в структуру новых элементов извне.
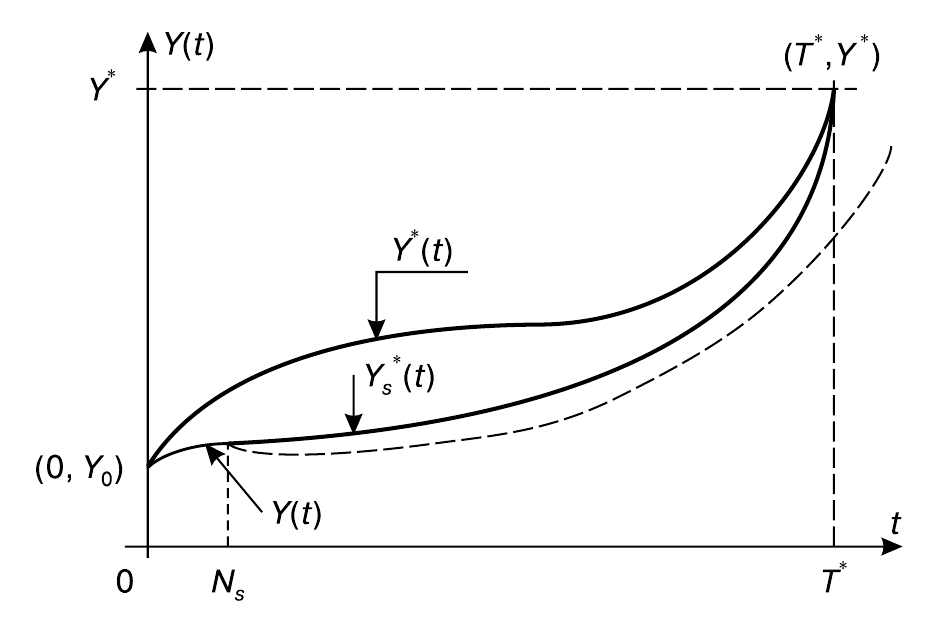
Разнообразию вариантов отвечает множественность названий для данного типа управления: реорганизация, модернизация, перестройка, самоорганизация и т.п. В качестве примеров можно привести смену схемы административного управления, сброс балласта с воздушного шара, забор или выдув воды из баков подводной лодки, пристройку к зданию и т.п. Ясно, что может встретиться случай, когда никакая комбинация наличных элементов не обеспечивает достижение поставленной конечной цели. Это означает невозможность и нецелесообразность управления по структуре, потенциал которой исчерпан.
Пятый тип управления — управление по целям. Выход снова видится не в безнадежном опускании рук, а в том, чтобы признать факт и сделать оптимистический вывод. Факт теперь состоит в том, что никакое использование имеющихся ограниченных средств не может реализовать желаемое состояние: данная цель в данных условиях нее достижима.
Остается сменить цель, понизив уровень притязаний, переориентироваться на достижимые сроки и (или) другие параметры конечного состояния. Это и есть пятый способ управления — управление по целям.
Можно различать цели, недостижимые в принципе. Обнаружение недостижимости некоторых таких целей является основанием отказаться от стремления к ним.
Существуют цели, недостижимые в одних условиях, но достижимые в других; есть цели, достижимость которых желательна, но не доказана, хотя и не опровергнута (искусственное мышление, антигравитация). Есть цели, достижимые, но не достигнутые из-за неэффективного или ошибочного управления. Однако определить, с каким именно из вариантов мы столкнулись, в некоторых случаях не является простым делом.
В практике управление по целям встречается нередко, особенно в административном управлении, менеджменте: ротация кадров, подыскивание посильной работы, переобучение, вообще управление персоналом. Следует только иметь в виду, что смена цели для любого индивида — болезненный процесс, тем более тяжелый, чем более высокого уровня цель приходится менять (осознание недостижимости цели иногда может даже сделать для субъекта бессмысленной саму дальнейшую жизнь). Так что этот метод требует осторожности.
Шестой тип управления — управление большими системами. Два первых типа основаны на совершенствовании модели системы, третий и четвертый — на изменении самой системы, пятый — на смене цели. Существует еще один фактор, влияющий на качество управления и требующий нового способа управления. Это своевременность управляющего воздействия. «Поезд уже ушел», «После драки кулаками не машут», «Силен задним умом» так отображает народный фольклор факт бесполезности запоздалого решения, даже самого лучшего во всех остальных смыслах.
Запаздывание с выбором наилучшего из возможных решений вызывается тем, что для оценки каждого из них нужно «проиграть» его на модели системы, а это требует определенного времени. Время же, отпущенное на выработку решения, может быть ограничено: по истечении этого времени управление теряет смысл. Управлять то надо в реальном масштабе времени, а моделировать управление — в ускоренном.
Может оказаться, что время, требующееся для нахождения оптимального решения, превосходит предельно допустимое для исполнения управляющего вмешательства. Тогда сама возможность найти оптимальное решение становится ненужной. А управлятььто необходимо! Это и требует выработки еще одного способа управления.
Оформим специальными терминами ситуацию, с которой мы столкнулись. Систему, для нахождения оптимального воздействия на которую достаточно информационного ресурса (модель адекватна), но недостаточно времени, будем называть большой системой, в противном случае — малой.
В качестве примера можно привести положение с советской экономикой, когда межотраслевой баланс подводился с задержкой в три-четыре года. Считалось, что это — одна из основных причин низкой эффективности управления экономикой страны.
Другой пример дал в свое время ВЦ новосибирского Академгородка, который реализовал очень развитую многокомпонентную модель для точного предсказания погоды на сутки вперед, но мощность тогдашнего ВЦ позволяла получить прогноз лишь через несколько суток. Ясно, что причиной того, что система оказывается большой, является не сама величина, громоздкость системы, а недостаточная скорость перебора и сравнения на модели вариантов управления, т.е. дефицит времени.
Поэтому первый, самый эффективный способ управления большой системой — превратить ее в малую, ускорив процесс моделирования. Например, заменив моделирующий компьютер более быстродействующим, распараллеливая алгоритм оптимизации, делегируя свои полномочия помощникам и т.д.
Но такой способ может натолкнуться на непреодолимые трудности (например, не существует более мощных машин, не оказалось подходящих кадров, не хватает финансов и т.д.). Поэтому в реальной практике часто употребляется другой, менее эффективный по качеству управления, но своевременно дающий результат. Не самое лучшее, но своевременное решение лучше, чем никакое или запоздалое.
Приходится отказываться от ожидания получения оптимального варианта и принимать первый получившийся удовлетворительный. Часто для получения слабого, но быстрого решения идут на различные упрощения модели (сокращение размерности, линеаризация и другие упрощающие аппроксимации, округление точных чисел и т.д.). Это вынужденные выходы из затруднительного положения для руководителя, действующего при дефиците времени. Иногда, правда, за этим скрывается неумение работать лучше…
Седьмой тип управления. Кроме первого типа управления, когда все нужное для реализации цели налицо, остальные рассмотренные типы управления связаны с преодолением факторов, мешающих достичь цель: нехватка информации об объекте управления (второй тип), сторонние мелкие помехи, слегка отклоняющие систему от целевой траектории (третий тип), несоответствие между эмерджентными свойствами системы и поставленной целью (четвертый тип), нехватка материальных ресурсов, делающая цель недостижимой и требующая ее замены (пятый тип), дефицит времени для поиска наилучшего решения (шестой тип).
Но в реальной жизни встречается еще одна ситуация — когда управлять текущими событиями приходится, но конечная цель непостижима, неизвестна.
Как же управлять, если отказаться от возможности объективно конкретизировать конечную цель? Так мы выходим на седьмой тип управления — управление при отсутствии информации о конечной цели.
Из определения цели логично вытекает, что при неопределенности конечной цели следует неопределенность и траектории движения к ней. А ведь управляющие воздействия при любом типе управления направлены на то, чтобы двигаться по этой траектории с максимально достижимой близостью к ней. Это стремление в данной ситуации можно реализовать по крайней мере двумя способами.
Первый способ состоит в том, чтобы дать субъективное, априорное определение конечной цели, а дальше действовать по предыдущим схемам.
Наглядный (но не единственный) пример этого дает нам управление крупными социальными системами. В чем смысл жизни? Какова цель социального развития? Готовые ответы этому дает идеология. Однако эти ответы являются лишь гипотезами. Разные сообщества придерживаются разных идеологий, субъективно отдавая предпочтение тому или иному идеалу. История уже показала нежизненность некоторых из них (рабовладельческий и феодальный строй), вскрыла острые недостатки других (тиранические, диктаторские режимы), утопичность третьих. Мы являемся свидетелями происходящего склонения общества к идеалам демократии. Но и в демократической идеологии некоторые основополагающие цели противоречивы. Например, идеи равенства и свободы несовместимы: при равенстве невозможна свобода, при свободе невозможно равенство. Попытка французской революции соединить их с помощью «братства» выглядит наивной или во всяком случае неконструктивной. Прикладной системный анализ предлагает в этом случае еще один идеал — равноправность и равноценность каждого индивида и улучшающее вмешательство как способ реализации этого идеала.
Интересным вариантом реализации демократического идеала (принятие решения большинством) является двухпартийная система. Одна из партий отдает приоритет свободе, другая — равенству. Оба идеала привлекательны, но несовместимы. Общество избирает «социалистов», т.е. начинает реализовывать равенство (в частности, проводит национализацию крупных отраслей экономики). Но процесс уравнивания неизбежно сковывает инициативу субъектов, и развитие общества замедляется. Когда это становится очевидным и нежелательным, общество избирает «либералов», которые начинают приватизацию и развязывают личную инициативу через свободу и частную собственность. Происходит развитие экономики, но усиливается неравенство между богатыми и бедными слоями общества.
Это вызывает нарастание напряженности в обществе, усиление ощущения «несправедливости». Тут-то и появляется возможность избрать во власть партию, проповедующую равенство. Конкретный пример — Англия.
И все же давайте признаем, что любая социальная идеология, утверждающая свое видение конечной цели, на самом деле предлагает гипотезу, истинность которой является вопросом веры в нее и последующей проверки на практике.
Имеется, однако, другой подход к управлению при невозможности явно определить конечную цель, но есть надежда, что она всетаки существует. Если это так, то должна существовать и траектория продвижения к ней. Она тоже неизвестна, но можно пытаться исследовать ближайшую окрестность вокруг текущего состояния и определить наиболее предпочтительное направление следующего шага в пределах этой окрестности. Затем сделать этот шаг и действовать в дальнейшем так же.
Такой способ реализуется в действительности в самых различных областях. В биологии он называется эволюцией и естественным отбором. В теории менеджмента (понимаемого широко) он называется инкрементализмом (внесение небольших, но обязательно улучшающих изменений). В математической теории оптимизации предложено несколько способов поиска экстремума функции нескольких переменных (покоординатные шаги типа метода Гаусса — Зейделя, случайный поиск, метод наискорейшего спуска по градиенту и т.п.). В социальных системах можно упомянуть раскритикованного марксистами Каутского с его лозунгом «Цель — ничто, движение к ней — все».
Конечно, на этом пути успех не гарантирован. Целевая функция, в существовании которой мы уверены, может оказаться многоэкстремальной, и мы можем попасть не в глобальный, а в локальный экстремум (примеры: тупиковые ветви эволюции живых популяций; выбор удовлетворительных, а не оптимальных решений в управлении социальными системами; застревание в локальных экстремумах при математической оптимизации и т.п.).
Приведенная в данной главе классификация типов управления не может быть абсолютной и универсальной (как, впрочем, и всякая классификация). Являясь моделью, она упрощенно описывает разнообразие реальных вариантов управления. В жизни могут встречаться случаи, когда в управлении одной системой используются одновременно или поочередно сочетания разных типов управления. С другой стороны, являясь моделью, данная классификация имеет целевой характер и для других целей могут потребоваться другие классификации. Например, в некоторых случаях различают автоматическое, полуавтоматическое (автоматизированное) и ручное управление; эти типы используются в управлении станками, самолетами, космическими пилотируемыми кораблями и т.д. Другая классификация потребуется, чтобы выделить менеджмент среди отличающихся от него типов управления: это не одноцелевое управление, не управление технической системой, не административное управление, не управление со стороны автомата и т.д.