Слово «алгоритм» происходит от имени выдающегося математика средневекового Востока Мухаммеда аль-Хорезми (787 – 850). Около 852 года он написал книгу, в которой им были предложены приёмы выполнения арифметических вычислений с многозначными числами.

В первой половине XII века книга аль-Хорезми в латинском переводе проникла в Европу. Переводчик (имя его неизвестно) дал ей название Algoritmi de numero Indorum («Алгоритми о счёте индийском»). Слово algorism (или algorismus) обрело значение способа выполнения арифметических действий посредством арабских цифр, то есть на бумаге, без использования абака. Именно в таком значении оно вошло во многин европейские языки.
Таким образом, сочинения по искусству счёта стали называться алгоритмати.
В 1684 году Готфрид Лейбниц в сочинении «Nova Methodvs pro maximis et minimis, itemque tangentibus…» впервые использовал слово «алгоритм» (Algorithmo) в ещё более широком смысле: как систематический способ решения проблем дифференциального исчисления.

Пользовался словом «алгоритм» и ещё один выдающийся математик – Леонард Эйлер, одна из работ которого так и называется – «Использование нового алгоритма для решения проблемы Пелля». Здесь видно, что Эйлер уже понимает алгоритм в ещё более широком смысле, а именно: как синоним способа решения задачи.

В 30-е годы XX века возникает научное направление «Теория алгоритмов», предметом исследования которого стала разработка универсальной алгоритмической модели. Наибольший вклад в теорию алгоритмов внесли английский математик Алан Тьюринг и русский математик Андрей Марков.

Алан Тьюринг в 1935-1936 годах создаёт теорию «логических вычисляющих машин». Разработанная им «машина Тьюринга» стала обязательной частью обучения будущих математиков и компьютерщиков. На одной из лондонских гостиниц мемориальная доска гласит: «Здесь родился Алан Тьюринг (1912 - 1954), взломщик кодов и пионер информатики».
Андрей Марков в 1947 году ввёл понятие «нормального алгоритма» и впервые систематически и строго построил общую теорию алгоритмов. Современные языки символьной обработки информации (Пролог) берут своё начало от нормальных алгоритмов Маркова.

Понятие алгоритма так же фундаментально для информатики, как и понятие информации. Поэтому в нём очень важно разобраться. Единого «истинного» определения понятия «алгоритм» не существует. Вот лишь некоторые из предлагаемых определений:
«Алгоритм – это всякая система счислений, выполняемых по строго определённым правилам, которая после какого-либо числа шагов заведомо приводит к решению поставленной задачи». (А. Колмогоров)
«Алгоритм – это точное предписание, определяющее вычислительный процесс, идущий от варьируемых исходных данных к искомому результату». (А. Марков)
«Алгоритм – строго детерминированная последовательность действий, описывающая процесс преобразования объекта из начального состояния в конечное, записанная с помощью понятных исполнителю команд». (Н. Угринович)
При изучении информатики чаще всего используют следующее определение алгоритма:
Алгоритм – понятное и точное предписание исполнителю выполнить конечную последовательность команд, приводящую от исходных данных к искомому результату.
Каждый человек в повседневной жизни выполняет огромное количество алгоритмов.
| Пример. Алгоритм «Заварка чая»: | Пример. Алгоритм «Приготовь яичницу»: |
|---|---|
|
|
Для разработки алгоритма необходимо иметь исходную информацию (данные) и представлять конечный результат (цель).
Полный набор данных – необходимый и достаточный набор данных для решения поставленной задачи (получения искомого результата).
Исполнитель алгоритма – это объект или субъект, для управления которым составлен алгоритм.
В качестве исполнителей могут быть как живые существа, так и технические устройства. В частности, автоматическим исполнителем алгоритмов по обработке информации является компьютер.
Очень часто исполнителем алгоритмов является сам человек. Мы выполняем алгоритмы, когда переходим улицу, готовим еду, делаем уроки, звоним по телефону и т.д.
Но между человеком и автоматическим устройством есть существенная разница. Если для человека имеют значение не только указания, которые даны в алгоритме, но и большой фактор заложен в степени эмоциональности изложения, то для компьютера или другого устройства имеет значение – понимает он данную команду или нет. Выполнив необходимые действия, алгоритмическое устройство прекращает работу.
Поэтому исполнителя, выполняющего команды определённого алгоритма без анализа действий и ситуаций, называют формальным исполнителем.
Иными словами работа исполнителя состоит в последовательном формальном выполнении команд алгоритма, что не предполагает анализа правильности их построения, а также результата выполнения.
Пример. Исполнители алгоритмов:

|

|

|

|

|
| Компьютер | Солдат | Телевизор | Дрессированный лев | Автомобиль |
Исполнителя алгоритма характеризует среда его «обитания» и система команд исполнителя (СКИ).
Среда исполнителя – обстановка, в которой функционирует исполнитель.
Система команд исполнителя (СКИ) – это вся совокупность команд, которую может выполнить исполнитель.
СКИ считается полной, если содержит весь минимально-необходимый набор команд, позволяющий построить любой алгоритм в том классе задач, на который ориентирован исполнитель.
Определённая последовательность действий исполнителя всегда применяется к некоторым исходным данным. Например: для приготовления блюда по кулинарному рецепту нужны соответствующие продукты (данные). Для решения математической задачи (решение квадратного уравнения) нужны исходные числовые данные (коэффициенты и уравнения).
Любой алгоритм должен удовлетворять четырём основным свойствам:
Конечность алгоритма означает, что за конечное число шагов должен быть получен результат. Поэтому иногда это свойство называют результативностью.
Пример. Пусть имеется последовательность команд:
Легко догадаться, что данная последовательность команд будет выполняться бесконечно и поэтому алгоритмом не является.
Дискретность означает, что алгоритм должен быть разбит на последовательность отдельно выполняемых шагов.
Пример. Пусть необходимо решить следующий пример: (80+10)-5*(3+5)=
Запишем алгоритм решение примера, разбив его на шаги:
В результате выполнения алгоритма получим 50. Алгоритм будет выполняться только при условии одного действия за раз.
Понятность алгоритма означает, что алгоритм должен содержать только те команды, которые входят в СКИ.
Пример. Рассмотрим алгоритм:

Очевидно, что он легко может быть выполнен 10-летней девочкой, которая понимает все команды, входящие в данный алгоритм. Однако, для 10-месячного малыша данный алгоритм будет непонятен.
Точность алгоритма означает, что любая его команда должна определять однозначное действие исполнителя. Иными словами, алгоритм не должен быть рассчитан на принятие каких-либо самостоятельных решений исполнителем.
Пример. Рассмотрим следующий алгоритм, описывающий, как добраться до стадиона:

Данный алгоритм не уточняет, какое расстояние нужно пройти прямо, в какую сторону повернуть, на какой автобус сесть, поэтому разные исполнители будут выполнять его по-разному и цель вряд ли будет достигнута.
Для успешной работы алгоритма необходимо также, чтобы имелся полный набор исходных данных, необходимый для его выполнения. Если исходные данные неполные, то либо задачу вообще нельзя решить, либо она будет иметь неоднозначное решение.
Пример. Полный набор исходных данных
Пусть вы пришли в магазин самообслуживания и решили подсчитать стоимость предполагаемых покупок, чтобы узнать, хватит ли вам денег. Вам нужно купить 2 кг сахарного песка, 3 кг муки и 2 батона хлеба. Тогда для вычисления общей стоимости вам надо:
Если по какой-либо причине не будет вывешен ценник хотя бы для одного из продуктов, то данная задача не сможет быть решена.
Для представления алгоритмов используют несколько способов:
Самый простой способ – словесный – это способ записи алгоритма на естественном языке, но с тщательно отработанным набором слов и фраз, не допускающих повторений, синонимов, двусмысленности, лишних слов. Допускается использование математических символов.
Пример. Алгоритмы, записанные словесным способом:

|

|
| Поваренная книга | Инструкция по эксплуатации телевизионного приёмника |
При графическом способе описания алгоритма осуществляется с помощью блок-схем.
Блок-схема - это графический способ представления алгоритма, каждое действие при этом осуществляется рисованием последовательности геометрических фигур, каждая из которых подразумевает выполнение определенного действия алгоритма. Порядок выполнения действий указывается стрелками.
В таблице приведены наиболее часто употребляемые блоки:
| № | Наименование символа | Символ | Отображаемая функция |
|---|---|---|---|
| 1 | Блок вычислений |

|
Вычислительное действие или последовательность вычислительных действий |
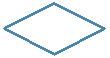
| 2 | Логический блок |
|
Выбор направления выполнения алгоритма в зависимости от некоторых условий |
| 3 | Блок ввода-вывода |

|
Общее обозначение ввода или вывода данных |
| 4 | Начало-конец (вход-выход) |

|
Начало или конец алгоритма |
Программный способ – это запись алгоритма на языке программирования (в виде компьютерной программы).
Существует три способа организации действий исполнителя: следование, ветвление, циклы.
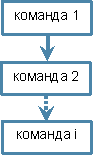
Следование – это способ организации действий, при котором команды следуют одна за другой, последовательно, образуя, так называемую серию команд.
Порядок выполнения: команды выполняются последовательно; каждая следующая команда выполняется только после выполнения предыдущей.
Особенностью выполнения данной конструкции является тот факт, что следование команд в серии определяется составлением алгоритма и на этапе выполнения не меняется. Это означает, что сначала выполняется, например, команда 2, а потом команда 3.
Алгоритмическая конструкция – линейная.
Запись конструкции:
| Словесная форма | Блок-схема |
|---|---|
|
----------------
команда 1; команда 2; ---------------- команда i; ---------------- |
|
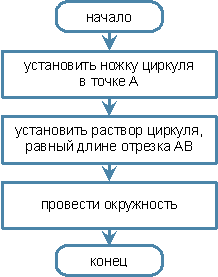
Пример. Алгоритм «Окружность»
| Словесная форма | Блок-схема |
|---|---|
|
|
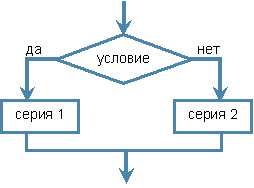
Ветвление – это способ организации действий, при котором выполняется та или другая серия команд в зависимости от условия.
Порядок выполнения: на первом шаге проверяется условие. Если оно истинно, то выполняется серия 1, и на этом выполнение команды ветвления заканчивается. Если условие ложно, то выполняется серия команд 2 и на этом выполнение команд ветвления заканчивается.
Особенностью выполнения команды является то, что из двух предложенных серий команд обязательно будет выполнена только одна: либо первая, либо вторая. Ни при каких условиях не могут быть выполнены обе. Серия 2 может отсутствовать и тогда конструкция ветвления является сокращённой. В этом случае, если условие окажется ложным, никакие действия не будут выполнены.
Алгоритмическая конструкция – ветвление.
Запись полной конструкции:
| Словесная форма | Блок-схема |
|---|---|
|
|
Запись сокращённой конструкции:
| Словесная форма | Блок-схема |
|---|---|
|
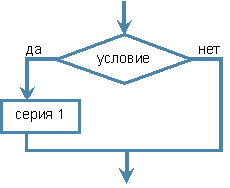
|
Пример. Алгоритм «Погода»
| Словесная форма | Блок-схема |
|---|---|

|
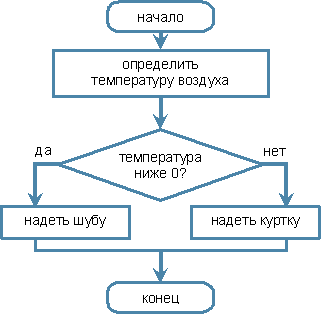
|
Цикл – это способ организации действий, при котором одна и та же серия команд выполняется неоднократно. Количество повторений зависит от условия.
Алгоритмическая конструкция – цикл.

Цикл с предусловием (цикл «пока»):
| Словесная форма | Блок-схема |
|---|---|
|
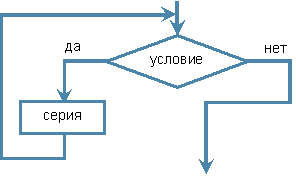
|
Порядок выполнения: на первом шаге проверяется условие. Если оно истинно, то выполняется серия команд, составляющая тело цикла и далее опять – проверка условия и т.д. Повторение выполнения тела цикла происходит до тех пор, пока условие истинно. Если условие ложно, то происходит выход из цикла.
Особенностью выполнения серия команд, составляющая тело цикла выполняется как единое целое, от первой команды до последней, и только на следующем шаге проверяется условие входа в цикл. Условие определяет количество повторений. Если оно ложно с самого начала исполнения команды цикла, то количество повторений будет равно 0. Условие и серия команд (тело цикла) должны формироваться таким образом, чтобы избежать ситуации зацикливания.
Цикл с постусловием (цикл «до»):
| Словесная форма | Блок-схема |
|---|---|
|
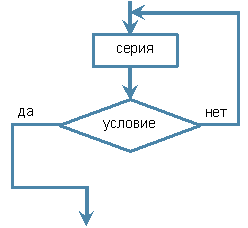
|
Порядок выполнения: на первом шаге выполняется серия команд, далее проверяется условие. Если оно ложно, то выполняется серия команд, составляющая тело цикла и далее опять – проверка условия и т.д. Повторение выполнения тела цикла происходит до тех пор, пока условие ложно. Если условие истино, то происходит выход из цикла.
Особенностью выполнения заключается в том, что тело цикла всегда выполняется хотя бы один раз.
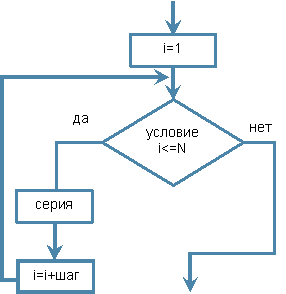
Цикл с параметром (цикл со счётчиком):
| Словесная форма | Блок-схема |
|---|---|
|
|
Порядок выполнения: данный цикл предусматривает присвоение параметру цикла i последовательных значений от начального 1 до конечного N с определённым шагом и выполнение операторов цикла при каждом из них.
Особенностью выполнения заключается в том, что заранее указывается количество повторений цикла. Однако если заданное конечное значение меньше начального, то тело цикла не выполняется ни разу.
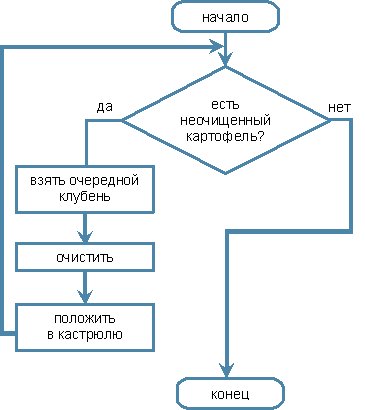
Пример. Алгоритм «Картофель»
| Словесная форма | Блок-схема |
|---|---|
|
|