Часто недостающую информацию о системе можно получить только из самой системы, проведя специально спланированный для этого эксперимент. Содержащуюся в протоколе эксперимента информацию извлекают, подвергая полученные данные обработке, преобразованию в форму, пригодную для включения ее в модель системы. Завершающим действием является коррекция модели, включающая полученную информацию в модель.
Легко воспринимается, что эксперимент нужен для совершенствования модели. Важно понять также, что эксперимент невозможен без модели. Они находятся в одном цикле. Однако вращение по этому циклу напоминает не вращающееся колесо, а катящийся снежный ком — с каждым оборотом он становится все больше, весомее.
Разнообразие экспериментов можно упрощенно описать их классификацией. Если мы не вмешиваемся в ход событий, а только регистрируем, что происходит на входах и выходах интересующей нас системы, то опыт называется пассивным экспериментом (или наблюдением). Если же мы не только созерцаем (и фиксируем) происходящее на входах и выходах, но и воздействуем на некоторые из них (одни намеренно поддерживая неизменными, другие — меняя должным образом), то опыт называется активным (или управляемым) экспериментом. Как и любая классификация, эта лишь приближенно описывает реальность. В абсолютно чистом виде эти два эксперимента невозможны: активный — потому, что все входы и выходы контролировать невозможно (некоторые даже неизвестны), пассивный — потому, что всякое измерение и наблюдение — взаимодействие, и вовсе не вмешаться в получаемый результат нельзя.
Ближайшими реальными, близкими к идеальным, экспериментами являются активный лабораторный опыт и пассивные наблюдения в астрономии, истории, археологии, психологии и т.п.
Еще одна важная классификация — деление экспериментов на прямые и косвенные. Прямой эксперимент — это наблюдение непосредственно той характеристики, которая нас интересует. Иногда интересующая нас характеристика не поддается прямому измерению, но есть наблюдаемая величина, связанная с нею, из наблюдений которой можно извлечь нужную нам информацию; это и будет косвенное наблюдение. Деление измерений на прямые и косвенные важно потому, что их надо обрабатывать по-разному, даже если они описаны в одинаковой шкале.
Осуществившиеся результаты эксперимента фиксируются в виде протокола наблюдений. Эта запись — не сам эксперимент, а описание его результата, т.е. его модель. Понимая термин «язык» широко, можно сказать, что протокол наблюдений — это запись результатов эксперимента на некотором языке. Разнообразие экспериментов таково, что одним языком не обойтись; существует несколько таких языков, называемых измерительными шкалами. Следует ознакомиться с ними, так как в практике придется иметь дело с обработкой данных в разных шкалах, а делать это нужно пооразному для каждой шкалы. Как в любом языке, неправильно построенная фраза теряет смысл, так и неправильно преобразованные данные эксперимента не несут ожидаемой информации.
На примере измерительных шкал можно проследить явление, характерное для всех языков: начиная с универсального, но малоинформативного языка, можно, включая, присоединяя к нему дополнительную информацию, получать все более и более информативные языки, вплоть до наиболее математизированного.
1. Шкала наименований (номинальная, классификационная). Простейшей моделью разнообразия является классификация. Она и положена в основу шкалы наименований. Измерение в этой шкале состоит в том, чтобы, произведя наблюдение классификационных признаков объекта, определить, к какому классу он относится, и записать это с помощью символа, обозначающего данный класс. Фамилии, диагноз заболевания, номера домов, автомобилей, игроков спортивных команд, названия цветов, адреса и т.д. — примеры наблюдений в номинальной шкале.
Поскольку единственным отношением, определяющим шкалу, является отношение эквивалентности (объект либо принадлежит к данному классу, либо нет), то единственной допустимой операцией над данными в этой шкале является проверка на совпадение.
Сравнивать между собой данные в номинальной шкале, полученные разными исследователями, можно, только если они пользовались одинаковым разбиением на классы (число классов и границы между ними должны совпадать). Отличаться могут лишь наименования классов и порядок их перечисления, как не нарушающие природной структуры данных.
2. Шкала порядковая (ординальная, ранговая). Если ввести между классами номинальной шкалы дополнительное отношение порядка (предпочтения), получится новая, усиленная в информационном смысле шкала, называемая порядковой или ординальной. Примерами наблюдений, регистрируемых в порядковой шкале, являются: армейские и чиновничьи звания, школьные оценки, магнитуда землетрясений (шкала Рихтера), твердость минералов (шкала Мооса), сила ветра (шкала Бофорта), призовые места в соревнованиях. Допустимое преобразование теперь дополняется операцией проверки предпочтения. Разновидностями предпочтений являются упорядочивание при наличии стандартных опорных образцов (например, шкала Мооса основана на десяти конкретных минералах разной твердости), при нечетко заданных образцах (шкала силы ветра, школьные оценки), при отсутствии образцов (спортивные соревнования, музыкальные конкурсы). Кроме шкал совершенного порядка, однозначно определяющих предпочтения (нумерация очередности, воинские звания и т.п.), существуют шкалы квазипорядка, когда некоторые элементы упорядоченного ряда неразличимы, а также шкалы частичного порядка, когда имеются несравнимые между собой пары классов. В порядковых шкалах не существует понятия расстояния между классами, поэтому любые преобразования, сохраняющие порядок («монотонные») не влияют на информативность данных.
3. Шкала интервалов (разностей). Если упорядочение объектов можно выполнить настолько точно, что известны расстояния между любыми двумя из них, то измерение станет заметно более информативным, чем в шкале порядка. Естественно выражать все расстояния в единицах, хотя и произвольных, но одинаковых по всей длине шкалы. Это означает, что объективно равные интервалы измеряются одинаковыми отрезками шкалы, где бы они на ней ни располагались.
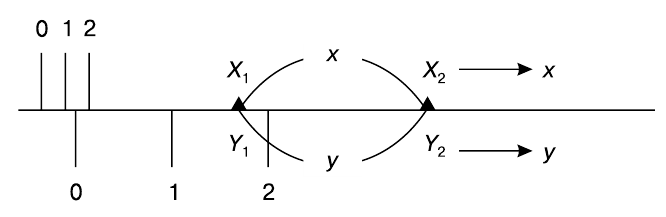
В итоге оказывается, что у нашей новой шкалы — шкалы интервалов — начало отсчета и единица длины интервала произвольны. Примеры наблюдений, фиксируемых в шкале интервалов: температура (шкалы Цельсия, Фаренгейта, Кельвина); летоисчисление (от Рождества Христова, от переезда Мухаммеда в Медину — на 622 года позднее, от императорской династии в Китае — на 5000 лет раньше); высота местности (от уровня моря; Голландия почти вся имеет отрицательную высоту).
Единственной новой допустимой операцией первичной обработки над данными в новой шкале является вычитание, т.е. определение интервала между двумя отсчетами. Например, если сказать, что температура увеличилась в два раза при нагреве от 9° до 18° по Цельсию, то для привыкших пользоваться шкалой Фаренгейта это будет звучать весьма странно, так как в этой шкале температура изменится от 48.2° до 64.4°. Операция деления для данной шкалы недопустима. Только интервалы имеют смысл настоящих чисел. Над ними (вторичная обработка) уже можно выполнять любые арифметические действия, а также статистические и другие процедуры.
4. Шкала циклическая (периодическая, разностей). Есть специальный вид интервальной шкалы, который характерен тем, что она замкнута на себя, т.е. после прохождения определенного периода ее значения повторяются. Примерами являются: угловые направления из одной точки (шкала компаса, роза ветров), время суток (циферблат часов), фаза периодических колебаний (в градусах или радианах), географическая долгота (в градусах). Все сказанное об интервальной шкале относится и к циклической. Чтобы не возникло недоразумений, отметим, что сложение часов — не сложение самих временных отметок (что является недопустимой операцией), а сложение временных интервалов, т.е. вторичная обработка. Надо еще помнить об условности начала отсчета (например, при переходе на зимнее время, при пересечении линии смены дат и т.п.). Данную шкалу еще называют шкалой разностей, так как она инвариантна к сдвигу на интервал, называемый периодом шкалы.
5. Шкала отношений. Введение еще одного определяющего отношения придает дополнительное усиление измерениям. Потребуем, чтобы не только отношения величин одного интервала в разных шкалах были константой, где бы этот интервал ни находился, что характерно для шкалы интервалов, но чтобы и отношения значений одной и той же величины, измеряемой в разных шкалах, тоже были константой, какое бы место эта величина ни занимала в реальности. Получаемая шкала именуется шкалой отношений. При этом, хотя единица измерений остается произвольной, нулевая отметка становится абсолютной, несдвигаемой. Примерами величин, природа которых соответствует шкале отношений, являются: длина (измеримая в см, футах, аршинах, км и т.д.); вес (кг, фунты, пуды, тонны и т.д.); объем (м3, баррели, литры и т.д.); деньги (рубли, доллары, евро, йены и т.д.). Данные в шкале отношений в еще большей степени становятся числами: в первичной обработке с ними имеют смысл любые арифметические операции, то же можно делать и во вторичной.
6. Абсолютная шкала. Предыдущие «числовые» шкалы (интервальная и отношений) имели степени свободы: интервальная — две (произвольный нуль и единицу), отношений — одну (фиксированный, несдвигаемый нуль и произвольную единицу). Характерно, что «числовые» возможности данных в этих шкалах были ограничены: в интервальной шкале — операцией разности, в шкале отношений — арифметическими операциями.
Рассмотрим такую шкалу, которая имеет и абсолютный нуль, и абсолютную единицу. Эта шкала не имеет степеней свободы, она единственна, уникальна. Именно такими качествами обладает числовая ось, которую естественно назвать абсолютной шкалой. Важная отличительная особенность абсолютной шкалы состоит в том, что значения данных в ней не имеют размерности, наименований, ее единица абсолютна («штука»). Это придает данным в этой шкале особый статус (в английском языке их называют pure numbers — чистые числа) — с ними можно производить такие операции, которые недопустимы с поименованными числами. Их можно употреблять в качестве показателя степени, основания логарифма, над ними допустимы любые тригонометрические и другие трансцендентные преобразования.
Обсужденные выше шесть измерительных шкал не исчерпывают многообразия языков, на которых можно говорить о разнообразии реальности. Но они являются базовыми: остальные шкалы — производные от них, учитывающие некие сторонние, побочные, специфические условия.
До сих пор речь шла о шкалах, основанных на четкой классификации: элемент либо принадлежал к классу, либо нет. Реальная жизнь привела к необходимости рассмотрения случаев, когда требование жесткой эквивалентности не выполняется, т.е. когда элемент может одновременно принадлежать к двум и более классам. Для описания таких ситуаций разработаны два подхода.
Первый основан на теории расплывчатых (нечетких) множеств. В этой теории принадлежность к классу описывается функцией принадлежности, которая характеризует степень уверенности, с которой мы относим объект к классу. Например, в какой степени сорокалетний человек относится к классу «молодые люди», а в какой степени к «немолодым»? В этой теории измерительной шкалой является шкала значений функции принадлежности.
Второй подход состоит в учете того, что распределения вероятностей классифицируемых переменных могут перекрываться. Принимая решение о принадлежности величины к тому или другому классу, мы рассекаем область значений переменной на четкие классы, в результате чего появляются вероятности ошибок. Обработкой случайных переменных занимается развитая область знаний — математическая статистика.
При осуществлении эксперимента получаемый информационный «урожай» зависит от ряда факторов:
Значимость этих факторов различна в разных опытах, поэтому развиты специальные теории о том, как повысить качество выводов в зависимости от конкретной комбинации факторов. Практика показывает, что специалисты часто, пытаясь облегчить себе задачу, пренебрегают некоторыми тонкостями анализа данных, искренне полагая, что они несущественны. Типичным примером является нередко применяемая «оцифровка» качественных данных — классам в порядковой и номинальной шкалах присваиваются номера, а дальше эти номера обрабатываются не как символы, а как числа, с помощью арифметических операций. Но ведь это недопустимые операции для этих шкал! Другой пример — ослабление данных для приведения их к однообразию. В таблице с разношкальными данными сильные шкалы огрубляются до самой слабой (обычно порядковой), так что протокол эксперимента становится одношкальным, что облегчает обработку. В отличие от оцифровки, здесь происходит не навязывание чуждой информации, а отказ от части полезной. Это тоже снижает качество выводов.
Главной задачей при изложении данного этапа является направить внимание пользователя услуг по проведению экспериментов на проверку того, а не случилось ли использования недопустимых операций при обработке данных. Например, все числовые шкалы оперируют цифрами. Но мы уже знаем, что цифры в шкале интервалов, отношений и абсолютной должны обрабатываться по-разному. При приемке заказа рекомендуется посмотреть, нет ли в алгоритме обработки недопустимых операций.
Еще один важный момент следует иметь в виду — речь идет о согласовании информационной силы измерительной шкалы с информационным потенциалом наблюдаемого явления. Чем сильнее шкала, тем больше «информационный урожай» с эксперимента. Поэтому каждый экспериментатор старается использовать как можно более сильную шкалу. Но ведь нельзя наблюдение с произвольно устанавливаемым нулем считать принадлежащим к шкале отношений. Таким образом, при прямых наблюдениях желательно шкалу измерений делать посильнее, но не сильнее самой природы явления.
Дело еще более осложняется при косвенных наблюдениях. Наблюдаемая величина, косвенно связанная с интересующим нас ненаблюдаемым явлением, может принадлежать к любой, в том числе и к самой сильной шкале; тогда как информационный потенциал самого явления может быть существенно ниже. Как обрабатывать данные эксперимента? Ответ состоит в том, чтобы при обработке косвенных данных, в сколь бы сильной шкале они ни фиксировались, не употреблять операций, недопустимых в шкале, отвечающей природе исследуемого явления.