Рано или поздно наступает момент, когда дальнейшие действия могут быть различными, приводящими к разным результатам, а реализовать можно только одно действие, причем вернуться к ситуации, имевшей место в этот момент, уже нельзя. Наступает момент выбора.
Естественно, выбирается тот вариант, который наиболее (по мнению выбирающего) соответствует его цели. Именно выбор является реализацией целенаправленности всей деятельности субъекта. Способность сделать правильный (т.е. наиболее приближающий к осуществлению цели) выбор — очень ценное качество, присущее людям в разной степени. Великие полководцы, выдающиеся политики, гениальные инженеры и ученые, талантливые администраторы отличались и отличаются от своих коллег или соперников прежде всего умением принимать лучшие решения, делать лучший выбор.
Для «жестких» задач выбора разработана вполне строгая формальная методика нахождения наилучшего в заданных условиях (оптимального) решения. В случае «рыхлой» постановки задачи осознана неединственность решения и разработана «мягкая» технология поиска приемлемых, «улучшающих» вмешательств. В промежуточных случаях сочетаются (в разных пропорциях) интеллектуальные способности человека решать неформальные задачи и подходящие формальные методы математики и компьютерного моделирования (системы поддержки принятия решений, экспертные системы, базданных, автоматизированные системы управления и т.п.).
На предыдущих этапах системного анализа было подготовлено все необходимое для выбора: есть множество альтернатив, на котором предстоит сделать выбор; определены цели, ради достижения которых производится выбор; выбраны критерии для сравнения альтернатив по степени их пригодности для достижения целей. Данный же этап посвящен рассмотрению проблем собственно выбора, т.е. процесса принятия решений.
В самом общем виде выбор можно определить как целевое сужение множества альтернатив: часть этого множества $Х$ признается приемлемым, остальные отвергаются. Обычно стараются свести к одной-единственной альтернативе, но иногда это неразумно или даже невозможно.
Стремление к тому, чтобы наш выбор был как можно более правильным, побуждает к построению некоторой теории выбора, которая предлагала бы средства синтеза алгоритмов выбора и их анализа (сравнения). Однако попытки построить «общую теорию принятия решения» наталкиваются на серьезные трудности. Множественность задач выбора. Выясним разнообразие ситуаций выбора с помощью метода морфологического анализа. В соответствии с этим методом перечислим факторы, определяющие характер выбора, и их градации.
Уже учет только перечисленных факторов дает 800 вариантов задач выбора. Каждый из них требует специального сочетания методов из разных областей знаний. Становится понятным, почему нет (и не может быть) универсальной теории принятия решений. И действительно, разработаны различные теории для разных типов ситуаций выбора: теория оптимизации (определенность исхода, односторонний выбор, одно- или многокритериальные задачи); математическая статистика (стохастическая неопределенность); теория размытых множеств (расплывчатая неопределенность); теория коллективного выбора (многосторонний выбор при единстве цели); теория игр (многосторонний конфликтный выбор) и т.д. Для некоторых ситуаций пока не найдено алгоритмических решений (неявное задание критериев, незнание существенных параметров и т.д.), когда приходится действовать «по интуиции», «согласно здравому смыслу», «наугад» и пр.
Представляется полезным дать обзор наиболее часто встречающихся ситуаций выбора и употребляемых в этих случаях методов принятия решений.
Критериальный выбор. Основой данного варианта выбора является предположение о том, что каждую отдельно взятую альтернативу можно оценить конкретным числом (значением критериальной функции). Тогда сравнение альтернатив сводится к сравнению соответствующих им чисел. Пусть $x$ — некоторая альтернатива из множества $X$. Считается, что для всех $x$ может быть задана функция $q(x)$, которая называется критерием (критерием качества, условной функцией, функцией предпочтения, функцией полезности и т.д.) и обладает тем свойством, что альтернатива $x_i$ предпочтительнее альтернативы $x_j$ (будем обозначать это $x_i > x_j$ ), то $q(x_i) > q(x_j$).
Если теперь сделать еще одно важное предположение, что выбор любой альтернативы приводит к однозначно известным последствиям (т.е. считается, что выбор осуществляется в условиях полной определенности) и значение $q(x)$ численно выражает оценку этих последствий, то наилучшей альтернативой $x^*$ является, естественно, та, которая обладает наибольшим значением критерия:
$$x^* = \arg[\max(q(x))].$$Задача отыскания $x^*$, простая по постановке, часто оказывается сложной для решения, поскольку метод ее решения (да и сама возможность решения) определяется как характером множества $X$ (размерностью вектора $x$ и принадлежностью его компонент к конечному, дискретному или континуальному множествам), так и типом критерия (является ли $q(x)$ функцией или функционалом, каким именно, заданным явно или неявно, в виде равенства или неравенства и т.д.). Университетский курс методов оптимизации, посвященный решению таких задач, является одним из самых объемных и сложных. Но сложности эти технические, а в принципе задача проста: нужно максимизировать критерий при заданных ограничениях.
Задача существенно усложняется при переходе от единственного к нескольким критериям. Правильнее даже будет сказать, что многокритериальная задача принципиально отличается от однокритериальной. Это проявляется уже на примере двухкритериальной задачи.
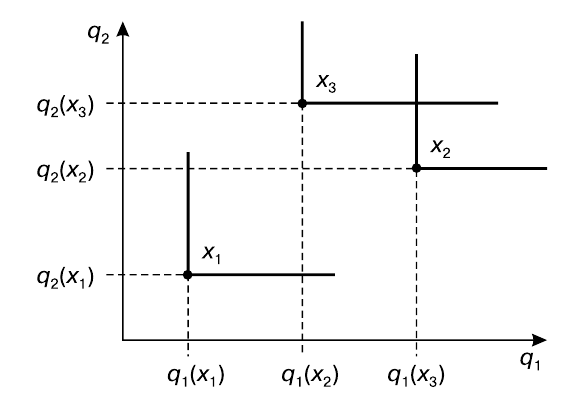
Если сравнивать альтернативы $x_1$ и $x_2$ или $x_1$ и $x_3$, то никаких сомнений не возникает, поскольку и $x_2$ и $x_3$ по обоим критериям $q_1$ и $q_2$ лучше $x_1$. Но как сделать выбор между $x_2$ и $x_3$? Каждый из них лучше другого по одному критерию и хуже — по другому. Были сделаны попытки решать многокритериальную задачу путем сведения ее к однокритериальной (или последовательности однокритериальных), так как способ решения последней очевиден. Было разработано несколько методов, из числа которых стали употребительными следующие.
Построение «суперкритерия», «глобального критерия» $q_0(x)$ как некоторой комбинации локальных критериев $q_1(x), …, q_k(x)$:
$$q_0(x) = f[q_1(x), q_2(x), …, q_k(x)].$$Наряду с техническими сложностями объединения критериев, измеряемых в разных шкалах (сложности решаемы искусственными приведениями их к одной шкале), все упирается в выбор упорядочивающей функции $f$: ее задание будет приводить к выбору единственной альтернативы, но при переходе к другой упорядочивающей функции выбор будет иным. Чувствуется наличие нежелательного, но неизбежного произвола.
Условная оптимизация, при которой выделяется один «наиболее важный» критерий, остальные переводятся в разряд условий, т.е. фиксируются на приемлемом для заказчика уровне. Вариантом такой задачи является задание условий в виде неравенств. И в этом случае налицо произвольность получаемого решения, которое зависит от задаваемых условий.
Метод уступок, при котором критерии упорядочиваются по важности, а затем оптимизация производится по наиболее важному критерию. После этого назначается уступка по этому критерию, т.е. величина, на которую мы согласны понизить достигнутое значение первого критерия, чтобы в пределах этой уступки максимально повысить значение второго. И так далее. Здесь произвол присутствует в виде упорядочения критериев и величин уступок по каждому из них.
Лексикографическое упорядочение. В отличие от метода уступок, критерии считаются настолько сильно отличающимися по важности, что применение следующего критерия производится только в том случае, если предыдущий дал неоднозначный ответ, и без всяких уступок. Термин «лексикографический» применен в связи с тем, что этот принцип используется в словарях: там упорядочение слов соответствует порядку букв алфавита в искомом слове.
Метод задания уровня притязаний. В отличие от предыдущих методов в данном случае производится не поиск лучшей (в том или ином смысле) альтернативы, а задание ее желательных качеств и проверка, есть ли среди наличных альтернатив $X$ именно такая. При положительном ответе желательно указать существующие превосходящие заданную альтернативы, при отрицательном — существующие ближайшие по заданным критериям.
Хотя через каждые два года проводятся международные симпозиумы Ассоциации многокритериального принятия решений (MCDM: MultyyCriteral Decision Making), где обсуждаются новые варианты перечисленных выше методов, отметим, что все эти методы суть попытки применить однокритериальное мышление к многокритериальному случаю. Инертность мышления заставляет искать единственно верное решение, тогда как в многокритериальном случае такового, как правило, не существует.
Между тем адекватное решение многокритериальных задач было предложено еще в начале прошлого века математиком-экономистом Парето. Оно основано на том, что предпочтение одной альтернативе перед другой следует отдавать, только если первая по всем критериям лучше второй. Если же предпочтение хотя бы по одному критерию расходится с предпочтением по другому, то такие альтернативы признаются несравнимыми и одинаково предпочтительными.
Альтернатива, по всем критериям уступающая другой, называется доминируемой, а превосходящая ее по всем критериям — доминирующей. Теперь выбор в многокритее риальном случае становится очевидным: следует отбросить все доминируемые альтернативы. Но результат в общем случае становится неоднозначным.
Множество недоминируемых альтернатив называют паретовским множеством. Это и есть адекватное решение многокритериальной задачи.
Однако в реальной жизни можно реализовать только один вариант, и возникает вопрос: какой из вариантов из паретовского множества надо осуществлять? Встает вопрос о выборе на паретовском множестве. Его элементы несравнимы, т.е. одинаковы в том смысле, что лучше их по всем критериям нет, поэтому выбрать можно любой. Есть разные способы выбора в такой ситуации.
Волевой выбор: лицо, принимающее решение, самостоятельно определяет, какой вариант осуществлять, либо прибегает к услугам экспертов.
Случайный выбор: решение отдается воле случая (бросание монеты, игральной кости и т.п.).
Введение дополнительных критериев, различающих альтернативы из паретовского множества (в частности, применение глобального критерия или введение нового).
Интересный вариант выбора на паретовском множестве предложили Д.С. Хэммонд, Р.Л. Кини, Г. Райффа.
Трудность сравнения и выбора между данными, выраженными в различных измерительных шкалах, предлагается преодолевать методом «равноценного обмена». Идея состоит в том, чтобы сравнивать не сами данные (они в принципе несравнимы), а сопоставлять выигрыш или потери, которые получаются в результате предпочтения одного другому. Метод разработан для случая выбора среди нескольких альтернатив по совокупности нескольких критериев, — ситуации, типичной в управленческой практике. Метод можно изложить в виде следующего алгоритма:
Главной трудностью этой методики является определение стоимости изменения величины каждого критерия. Например, при выборе между рейсами разных авиакомпаний трудно осуществить обмен степени безопасности на удобство времени вылета. В таких случаях рекомендуется перейти к рассмотрению более легко сравнимых пар критериев. Может случиться, что сделав самые простые обмены, вы получите решение, и не потребуется ломать голову над сложными обменами.
Для многокритериальной задачи не существует единственно верного решения, есть некоторое (паретовское) множество приемлемых решений, из которых можно принять любое.
Выбор на основе парных сравнений. В реальной жизни часто встречаются случаи, когда никакие критерии не позволяют выделить «самую лучшую» альтернативу. Например, у боксера можно измерить вес, объем мышц, определить скорость реакции и т.д., но по этим данным нельзя предсказать, станет ли он чемпионом. В таких случаях критериальный язык теряет смысл, а с ним и соответствующие методы становятся неприменимыми.
Однако, хотя адекватная оценка отдельной альтернативы при этом невозможна, существует возможность поставить две альтернативы в такую соревновательную ситуацию, где они в реальности сравнили бы свои качества, и исход такого соревнования определит их порядок предпочтения. Примерами таких ситуаций являются турниры, конкурсы, бои — любые парные сравнения.
Если альтернатив больше, чем две, то возникает вопрос: как выделить среди них наиболее предпочтительную, если мы располагаем только результатами попарных сравнений? По поводу такой задачи созданы довольно разветвленные математические теории, поскольку множество альтернатив может быть конечным, счетным или непрерывным, а сами отношения между парами можно описывать пооразному. Для наших целей ограничимся представлением парных сравнений так называемым графом предпочтений.
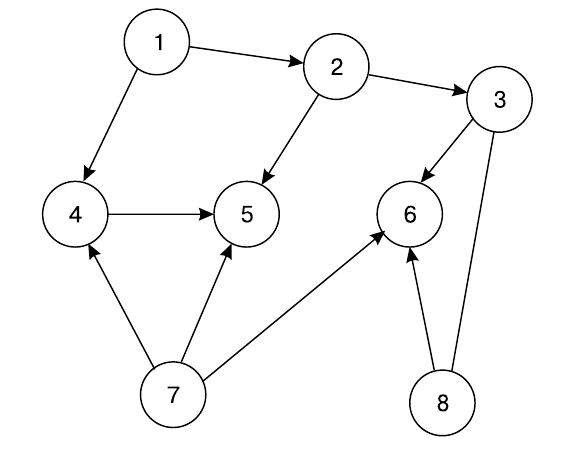
На рисунке:
Располагая таким протоколом наблюдений, можно выделить «самые лучшие» альтернативы. Для этого нужно определить критерий, кого считать «лучшим», и сделать это можно по-разному. Например, считать лучшим того, кто не проиграл ни разу. Тогда выделятся альтернативы 1, 7 и 8. Можно (для различения между ними) взять критерием количество выигранных «боев»; тогда лучшей станет 7-я альтернатива. Но может вызвать возражение проведение неодинакового числа боев для разных участников. Становится ясным, что для справедливого сравнения нужно провести встречи «каждого с каждым». Правда, и при этом может не оказаться «самого лучшего» по избранному критерию (например, не окажется того, кто не проиграл ни разу). Придется вводить другие критерии. Но главным препятствием для получения полного набора парных сравнений становится их большое количество — $N·(N–1)$ — при больших $N$, поэтому стало бы невозможным определение чемпиона мира ни по одному виду спорта. Правда, спортсмены разработали сокращенные, приближенные способы определения лидера — либо зональные соревнования с последующими сражениями между победителями зон, либо олимпийская система с выбыванием после первого переигрывания.
В реальной практике выбора встречаются случаи, когда и основное предположение теории парных сравнений не выполняется. Оно состоит в том, что порядок предпочтения в паре определяется только качествами сравниваемых альтернатив и не зависит от наличия или отсутствия других альтернатив. Если это не так (например, выбор между молотым кофе или в зернах зависит от наличия у вас кофемолки), то и язык парных сравнений теряет свое значение. Мало смысла строить теории сравнения на основе отношений между тремя, четырьмя и т.д. вариантами.
Предложен очень высокой степени абстракции язык «глобальных функций множеств». Он основан на понятии функции выбора. Эта функция $C(X)$ имеет своим «аргументом» все множество $X$ альтернатив $x$, а ее «значением» является некоторое подмножество множества $X$ (от пустого множества — отказ от предложенного, до всего $X$ — «беру все»). Предъявляя функции $C(X)$ те или иные требования, можно описывать различные ситуации выбора (в том числе и рассмотренные выше). Функция выбора оказалась малоизученным и весьма сложным математическим объектом; мы не станем углубляться в подробности, ограничившись приведенным упоминанием лишь для полноты картины.
Коллективный выбор. Из многочисленных задач выбора особый практический интерес представляет задача многостороннего принятия решения, когда выбор осуществляется не одним лицом, а группой лиц. При этом предполагается высшая степень согласия между членами группы относительно общей цели, выбор же приходится делать между вариантами средств достижения этой цели.
Типичным примером являются выборы на руководящий пост. Из нескольких кандидатов на этот пост можно избрать лишь одного, и каждый избиратель волен выразить свое личное предпочтение. Групповое решение $C_0(X)$ о наиболее предпочтительном кандидате $x_j = {x_1, …, x_k}$ получается путем «пересчета» всех индивидуальных предпочтений $C_1(X), C_2(X)…, C_N(X)$, где $N$ — число избирателей, в одно «коллективное» предпочтение $C_0(X)$ с помощью заранее объявленной и принятой всеми членами группы процедуры $f: C_0(X)=f[C_1(X),C_2(X), …, C_N(X)]$. Такую операцию называют процедурой голосования.
Представляет большой интерес выяснить, какими свойствами обладают процедуры голосования, как в силу их практической значимости, так и в связи с их разнообразием (функцию $f$ можно задавать пооразному). Тем более, что часто результаты голосования оказываются неожиданными, а иногда — нежелательными. При этом многие полагают, что сменив одно правило голосования на другое, можно избежать «неправильного» результата не только сейчас, но и в дальнейшем. Это заблуждение. Необходимо хорошо понимать природу голосования, чтобы правильно им пользоваться.
«Ум — хорошо, а два лучше» — гласит поговорка, предполагающая случай, когда оба ума (а по индукции — и большее число умов) с одинаковыми намерениями пытаются найти хороший выбор. При расхождении мнений в группе голосование является единственно возможным способом формирования «общего» мнения, коллективного решения. Но процедуры голосования обладают рядом свойств, в некоторых случаях дающих неожиданный или нежелательный результат. Перечислим такие свойства, назвав их парадоксами голосования.
1. Коллектив не всегда прав. Коллектив состоит из субъектов, каждый из которых может заблуждаться. Это приводит к тому, что голосование, даже единогласное, не гарантирует правильности принятого решения. Надо все же отметить, что за счет взаимной компенсации противоположных мнений вероятность ошибки коллективного мнения меньше, чем «среднеиндивидуального», но она остается не равной нулю. Известны случаи (Бруно, Галилей, Коперник и др.), когда один несогласный располагал истиной, а все остальные заблуждались. Таким образом, голосование предназначено не для добывания истины, а для согласования действий группы после голосования: все члены группы подчиняются принятому решению, даже если кто-то был с ним не согласен.
2. Возможность непринятия решения. Хотя голосование предназначается для принятия решения, любая процедура голосования может закончиться тем, что согласованные условия принятия решения не будут выполнены и, следовательно, решение не будет принято. Поясним это примерами. Скажем, «простое большинство» (50% плюс один голос) не сработает, если голоса четного числа голосующих разделятся поровну. Поправка «председателю — решающий голос» эту ситуацию обходит, но если нечетное число голосующих поделится так, что председатель окажется в половине, меньшей на один голос, то возникает вопрос: а чему равен «решающий голос»? При принятии «квалифицированным» большинством (в 2/3) на ученых советах бывали случаи, что защищающемуся не хватало малой доли голоса. Даже при принципе единогласия (консенсус, право вето) решение может быть не принято. Таково свойство всех процедур голосования.
3. Парадокс Кондорсе (так он назван по имени математика, разъяснившего этот парадокс). Суть парадокса в возможности цикличности графа предпочтений. Например, пусть каждая из трех фракций парламента, образующих большинство лишь попарно, выдвинула свой вариант законопроекта: $a$, $b$ и $c$. Или три парня заспорили, чья девушка лучше, и намерены решить этот вопрос голосованием. Если у этой троицы индивидуальные предпочтения таковы: ($a$>$b$>$c$), ($b$>$c$>$a$) и ($c$>$a$>$b$), то они попали в парадокс Кондорсе. Любая процедура либо закончится неприятием решения (так как при таких предпочтениях нет решения), либо при искусственном прерывании процедуры (например, при парном сравнении по олимпийской системе) исход будет зависеть от того, в какой последовательности будут рассматриваться пары.
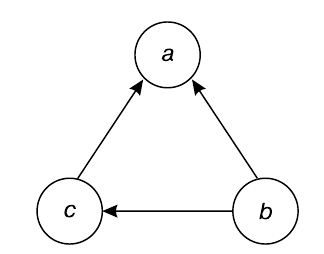
Иногда парадокс Кондорсе несущественен (если цикл предпочтения окажется в нижней части цепи альтернатив и не повлияет на выбор лидера). Если же его необходимо разрешить, то выход может быть в том, чтобы убедить одного из голосующих (сейчас это называется черным или белым «пиаром») изменить свое упорядочение альтернатив, не меняя первенства своей. Цикличность графа исчезнет, решение станет единственным.
4. Возможность победы меньшинства при мажоритарной системе голосования. Пусть решение принимается по большинству голосов (это и есть мажоритарная система). Оказывается, при этом существуют возможности законной победы меньшинства, да к тому же таких возможностей несколько. Первая — признание легитимными (законными) выборы при низкой (меньше 50%) явке избирателей. Решение автоматически предоставляется меньшинству. Трудно осуждать такую ситуацию, так как неучастие в выборах означает безразличие к тому, какое решение будет принято; пусть оно будет принято теми, кому это небезразлично. Но меньшинство может победить и при стопроцентной явке избирателей.
Вторая такая возможность — «растаскивание» голосов. Поясним это примером. Пусть одна коалиция обладает 60% потенциальных голосов, второй принадлежит 40% электората. Если первые выдвинут двух кандидатов, да еще равноценных, а вторые одного — победит меньшинство. Причины растаскивания голосов могут быть разными, а результат один.

Но меньшинство имеет шансы победить при стопроцентной явке и без растаскивания голосов. Снова поясним это примером. Пусть решение принимается большинством голосов в 2/3. Если в итоге победил представитель меньшинства, значит, на последнем этапе процедуры он набрал большинство. Если же участников последнего этапа голосования самих выбирали по тому же правилу, то возможна ситуация, изображенная на рисунке. Легко видеть, что победило меньшинство в 4/9 против 5/9. Для реализации такой возможности необходимо выполнение трех условий:
а) выборы должны быть многоступенчатыми (так как на каждой ступени решение принимается по большинству голосов);
б) меньшинство должно соблюдать дисциплину голосования (т.е. голосовать именно там, где требует организация всего дела: если хоть один из них поменяется местами с противником — по пунктирным стрелкам на рисунке, то у них ничего не выйдет);
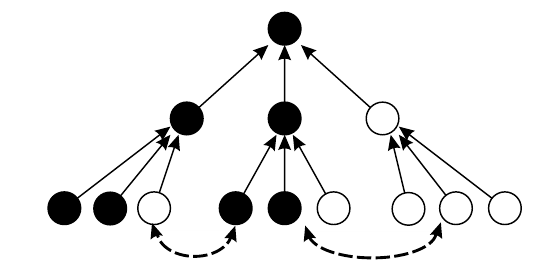
в) меньшинство должно быть достаточно многочисленным для обеспечения своего большинства на последнем этапе. Будь в нижнем ряду не 4, а 3 представителя меньшинства, снова ничего не получилось бы. Однако доля меньшинства может быть меньшей, если ввести дополнительные уровни голосования. Так, если дополнить схему еще одним уровнем, то пропорция меньшинства в 4/9 (44.4%) снизится до 8/27 (33.7%). Приведенная схема имеет не только теоретический интерес: многоступенчатые схемы голосования употребляются в жизни, например определенная конституцией двухступенчатая процедура выборов Президента США уже 4 раза из 43 приводила к победе кандидатов меньшинства. Последний раз — 2002 г. в соперничестве Буша и Гора: первый победил при наличии лишь 48% голосов на первичных выборах.
В другом виде парадокс мажоритарной системы заложен в избирательном законе Австралии. Интересное отличие состоит в том, что голосование там одноразовое (т.е. физически одноступенчатое). Однако, в отличие от нас, австралийский избиратель обязан не только указать, кому из кандидатов он отдает первенство, но и пронумеровать всех остальных кандидатов в порядке предпочтения. Обработка бюллетеней производится по следующей процедуре (в которой заложены уже известные нам парадоксы). Из всех бюллетеней извлекаются кандидаты, получившие высший балл (№ 1). Набравший необходимый для избрания пороговый процент голосов проходит в парламент. В случае, если никто из них такого процента не набрал (вариант растаскивания голосов!), счетная комиссия делает выборку всех кандидатов, получивших в бюллетенях второй номер, и повторяет проверку на превышение установленного порога и так далее до уровня, на котором кто-то достигнет порога (как видим, вместо физической многоступенчатости реализуется алгоритмическая). В австралийском парламенте бывают представлены партии, набравшие очень низкий процент голосов. Их шанс состоит в том, что голоса будут растащены на всех, кроме последнего, уровнях. А дисциплина голосования меньшинства состоит в том, что они выполняют указание своего руководства — ставить в бюллетенях своего кандидата на последнее место. Если процедура опустится на последний уровень — там мы все, плюс все те, кто поставил нас на последнее место. Этого вполне хватит для преодоления барьера на получение мандата.
5. Парадокс подавляющего большинства. Многие полагают, что при голосовании по принципу «один человек — один голос», чем больший процент голосов наберет альтернатива, тем более демократично принятое решение. Это — заблуждение. Видимо, такое впечатление основано на том, что политики чувствуют себя тем более уверенно, чем большая часть электората поддерживает их; тем в большей степени они ощущают себя представителями народа.
Парадокс состоит в том, что такое впечатление психологически понятно, так как основано на распространенных понятиях «наши и не наши», «свои и чужие»; но оно не имеет никакого отношения к понятию демократии. Какой бы высокий процент большинства ни был назначен для легитимности принятия решения, решение не является демократическим. Суть парадокса состоит в том, что данная процедура узаконивает принесение в жертву интересов одного всем остальным. При этом остальные забывают, что каждый из них может стать такой же жертвой. Таким образом, голосование по большинству и демократия — это просто разные вещи. Суть демократии не в том, чтобы все могли принять участие в прямых и тайных выборах. Решения могут приниматься как коллективно, так и единолично; а демократия состоит в том, чтобы на этапе исполнения решения были защищены интересы любого меньшинства, и прежде всего — основные права каждой отдельной личности (право на жизнь, право на собственность, право на свободу).
6. Парадоксы единогласия. Если определить демократию как защиту интересов каждого, то единственной демократической процедурой голосования оказывается единогласное принятие решений: свои интересы уже на этапе принятия решения может отстоять каждый, проголосовав против не подходящей для него альтернативы. Известны ответственные практические ситуации, в которых применяется принцип единогласия: право вето в некоторых парламентах; принятие решений Советом Безопасности ООН; выборы кардиналами очередного папы римского; вынесение вердикта о виновности подсудимого судом присяжных; принятие решений в акционерных обществах с неограниченной ответственностью. Этого же принципа настоятельно рекомендуется придерживаться в ходе прикладного системного анализа, так как его конечной целью является создание улучшающего вмешательства.
Однако и в этом случае возникают парадоксальные ситуации. Во-первых, иногда принцип единогласия («все за») подменяется принципом консенсуса («никто не против»), тогда как это разные вещи: воздержавшиеся отождествляются с согласными, отсутствующие исключаются из принимаемых во внимание. Вторая парадоксальная ситуация возникает, когда желательное решение никак не может набрать 100% голосов. Существует по крайней мере два способа попытаться достичь согласия в такой ситуации.
Первый — поиск компромисса. Если изобразить кругами множества приемлемых альтернатив трех лиц, принимающих решение, то недостижение единогласия объясняется просто отсутствием альтернативы, приемлемой для всех. Выход может состоять в том, чтобы кто-то (добровольно или под влиянием) расширил свой круг приемлемости так, чтобы появились взаимоприемлемые варианты (пунктирная линия их охватывает).
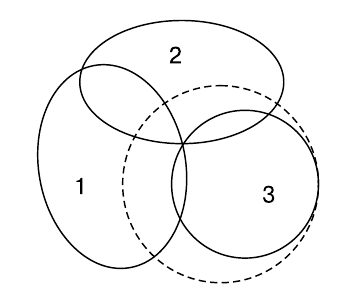
Второй способ можно назвать «способом лестницы». Если мы не можем запрыгнуть на сарай, мы подставляем лестницу и поднимаемся наверх по ступенькам. Так и здесь — можно попытаться подойти к желаемой, но никак сразу не достигаемой единогласно цели мелкими шагами, каждый из которых реализуется единогласно. Интересный пример такой реальной попытки приводит из своей практики Р. Акофф:
«Консенсус часто трудно достижим, но редко невозможен. Я обнаружил, что в трудных случаях очень эффективна следующая процедура. Первое — максимально уточнить формулировки альтернатив, между которыми консенсус не достигает выбора. Второе — коллективно построить тест эффективности альтернатив и консенсусом принять решение, что данный тест справедлив и что все согласны следовать его результату. Третье — провести тест и использовать его результат. Я смог успешно применить эту процедуру даже в таком случае, когда законодатели одного государства не могли прийти к согласию, вводить или нет смертную казнь за убийство. В результате обсуждения члены законодательного органа пришли к согласию, что все имеют одну цель — минимизировать число жертв убийств. Как только такое согласие было достигнуто, проблема была сведена к конкретному вопросу: уменьшает ли введение смертной казни число убийств? Все согласились, что необходимо провести исследование, отвечающее на этот вопрос. Такое исследование было проведено, и его результаты использованы (оно показало, что число убийств в ряде государств до и после отмены или введения смертной казни заметно и значимо не изменялось)».
Если же не удается достичь согласия не только по поводу самих альтернатив, но и относительно способа их проверки, то, по мнению Р. Акоффа, следует найти консенсусное решение, что же делать дальше. Интересно его наблюдение, что в таких случаях обычно принималось решение поручить выбор одному из авторитетных и ответственных лиц.
В целом парадоксы единогласия связаны с заблуждением о его природе. Бытует мнение, будто единогласие — признак верности решения: чем ближе мы к единогласию, тем ближе истина. Это заблуждение обсуждалось при рассмотрении первого парадокса. Само такое мнение основано на действительном повышении статистической надежности решения при увеличении объема выборки, что, однако, не гарантирует его абсолютной правильности.
Это не означает, что стремление к единогласию и консенсусу в принципе ошибочно и должно быть отвергнуто. Оно играет существенную роль в нашем мире. Но, если не принимать во внимание, что оно подавляет серьезные споры и возражения, это может вести к нежелательным последствиям типа коллективных патологий «кланомыслия» и «группомыслия». Оно ограничивает разнообразие мнений, а не расширяет его; сужает простор для дискуссий. Оно бывает необходимым, но является недостаточным для жизни в нашем сложном и изменчивом мире. Нужны другие способы мышления и действия. Ведь известно, что чем важнее и сложнее вопрос, тем труднее (или вообще невозможно) достичь всеобщего согласия.
7. Теорема Эрроу о невозможности. Самые общие теоретические результаты о коллективном выборе были получены Эрроу, за что он был удостоен Нобелевской премии по экономике. Наибольшую известность получила его «Теорема о невозможности». В ней вопрос стоит так: можно ли сказать что-нибудь содержательное обо всех процедурах выбора? Ответ: обо всех нет, а о процедурах «хороших», «приемлемых», т.е. удовлетворяющих определенным разумным требованиям, можно попытаться.
Из всевозможных функций $F$ от индивидуальных выборов $C_i(X)$ ($C_0(X) = F[C_1(X), ..., C_N(X)]$) выделим те, которые отвечают требованиям, выражающим наше понимание того, что такое «правильный», «справедливый», «хороший» коллективный выбор. Таких требований, по сути, всего четыре (в оригинале есть и другие, но они чисто технические математически):
а) все индивидуальные предпочтения $C_i(X)$ должны как-то быть учтены; не должно быть такого индивида, чье мнение принимается обязательным для всех, независимо от мнения остальных (функция $C_0(X) / C_1(X)$ называется «диктаторской», и это условие выражает нежелательность диктаторства);
б) если в результате группового выбора предпочтение было отдано какой-то альтернативе, то это решение не должно меняться, если кто-нибудь из ранее отвергавших ее изменил свое мнение в ее пользу (условие монотонности);
в) если изменения индивидуальных предпочтений не коснулись каких-то альтернатив, то в новом групповом упорядочении порядок этих альтернатив не должен измениться (условие независимости альтернатив). Поясним это требование примером. Пусть $C_0(X) = F[C_1(X), ..., C_i(X), ..., C_N(X)]$. Мысленно вернемся назад, изымем из урны бюллетень $i$-го избирателя и попросим его «еще раз подумать». Пусть он в своем предпочтении поменял местами двух кандидатов. Пересчитаем $C_0(X)$ с учетом другого варианта его бюллетеня. Результат может чаще всего остаться прежним. Но если по этим двум кандидатам ситуация была неустойчива и одного голоса оказалось достаточно, чтобы изменить ее, то будет справедливо, чтобы в новом упорядочении изменение коснулось только этих кандидатов и не задело остальных;
г) для любой пары альтернатив возможны такие два множества индивидуальных предпочтений, при которых порядок этих альтернатив противоположен («условие суверенности»).
Такова часть «Если…» в теореме Эрроу. Часть «То…» гласит (из-за чего она получила название «Теоремы о невозможности»): указанные требования несовместны, т.е. не существует процедур голосования, удовлетворяющих всем этим требованиям.
Это стало большой неожиданностью (ведь требования кажутся такими естественными и необходимыми!) и вызвало бурные дискуссии. Оказалось, что причиной такого результата являются упомянутые выше парадоксы, а на первое место вышел факт, что коллективный выбор может «застрять», закончиться непринятием решения, а единоличный, «диктаторский» выбор — никогда. Это привело к большому шуму вокруг теоремы о невозможности: «Наука доказывает слабость демократии», «Наука доказывает неизбежность диктатуры» и т.п. Ныне пыль осела (прошло много лет) и комментарии к теореме о невозможности можно сделать такие:
а) нравится это кому-то или нет — такова природа голосования;
б) теорема Эрроу — о голосовании, а не о демократии. Это разные вещи, и ее политическая интерпретация является подменой понятий;
в) непринятие решения приведет к потерям, а потери могут быть приемлемыми или нетерпимыми;
г) если потери допустимы, мы предпочитаем принимать решения коллективно, голосованием: это придает некий смысл нашей общественной деятельности;
д) если потери от непринятия решения нетерпимы, следует исключить саму возможность непринятия решения. Это можно сделать только одним способом — перейти к единоличному принятию решения, т.е. к диктаторской функции;
е) в самом по себе единоличном принятии решений нет ни плохого ни хорошего. Все зависит от конкретных условий. Например, отменить в армии принцип единоначалия — значит только ослабить боеспособность армии. Да и в обыденной жизни в коллективно неопределенной ситуации мы прибегаем к мнению авторитетов;
ж) обсуждение свойств процедур голосования не имеет никакого отношения к политике. Это лишь строгое логическое рассмотрение особенностей формул пересчета индивидуальных предпочтений в одно, называемое коллективным. А уж как использовать знание этих свойств в реальной жизни — это вопрос политики.
Принятие решений в социальной системе. До сих пор мы рассматривали принятие решений аналитически: есть множество альтернатив, из которых надо выделить одну, наиболее предпочтительную. И основное внимание уделялось внутренней, технической стороне дела: как надо делать такой выбор. Обнаружилось множество вариантов, и в каждой ситуации алгоритм принятия решений имел особенности, учитывающие специфику ситуации.
Принятие решений — важнейшая функция в управленческой деятельности. Управление есть осуществление изменений в управляемой организации. А организация — это некоторая структура с распределением прав и обязанностей, власти и ответственности. Поэтому принятие решений в такой системе должно происходить с учетом того, каковы полномочия лица, принимающего решения. А эти полномочия определены его положением в организационной структуре. При этом приходится учитывать позицию лица, принимающего решения как в структуре своей организации, так и в структурах внешних систем, куда наша организация входит как часть.
Начнем с рассмотрения специфики принятия внутренних решений лицом, входящим в некоторую организацию. Диапазон его решений в определенной степени ограничен его должностной инструкцией. Но какие решения на каком уровне иерархии должны приниматься? Желательная цель — минимизировать вероятность принятия ошибочных решений. Подверженность ошибке — неизбежная особенность любого субъекта, на любом уровне управленческой иерархии. Отсюда следует вывод, что решение должно приниматься на том уровне, где сосредоточена максимальная информация о ситуации, требующей вмешательства. И это не обязательно уровень высшего руководства в организации, что и является основой необходимости делегирования властных полномочий на нижележащие уровни иерархии.
Итак, стоит задача передачи права принятия решений на те нижестоящие уровни, которые наиболее компетентны в проблемной ситуации. Руководитель обычно неохотно идет на отдачу части своих полномочий подчиненным. Убедить его пойти на это можно несколькими способами. Главный — показать, что организация будет функционировать лучше, если предоставить работникам больше свободы в принятии решений. Работники в больших организациях обычно отчуждены из-за того, что у них нет права голоса, они не влияют на принятие решений, оказываются в значительной мере подобны роботам.
Другой важной особенностью внутренней среды организации для принятия решений является образованность работников. Чем более образованы работники, тем менее эффективно властное управление ими. Наглядным примером служат университеты, значительная часть работников которых имеют ученые степени. И никакой ректор не управляет университетом, решая, что и как должно преподаваться, как оцениваться, какие книги должны использоваться. Все важные для учебного процесса решения принимаются на нижних уровнях иерархии.
Еще один способ побудить высших руководителей делегировать полномочия подчиненным — ознакомить их с проблемами самого нижнего уровня, — пользователей. Руководители часто полагают, что их власть проявляется в том, чтобы выглядеть всезнающими и возвышенными; что общение с нижестоящими снижает их авторитет и статус; они часто и не желают знать, что происходит в самом низу. Полезный совет состоит в том, чтобы руководитель транспортной компании иногда ездил вместе с обычными пассажирами, директор магазина сам делал покупки в нем, и т.п.
Обратимся теперь к проблемам принятия решений, связанных с необходимостью взаимодействий с внешними управленческими структурами. Если внутренние проблемы вязаны с оптимизацией распределения прав и обязанностей между подчиненными, что находится во власти менеджера, то отношения с внешними структурами чаще всего сводятся к испрашиванию решений вышестоящих руководителей по вопросам, существенным для нижестоящей организации.
Взаимодействия с социальными системами бывают двух типов: либо они дают нам возможность сделать или получить что-то, чего без их содействия мы не можем иметь, либо они предотвращают такую возможность. Иными словами, системы, с которыми мы взаимодействуем, расширяют или сокращают число наших допустимых действий: либо позволяют, либо запрещают что-то сделать. Хотя существуют системы, функционирование которых носит преимущественно ограничительный характер (напр., тюрьма) или преимущественно расширительный (напр., библиотека), но многие совмещают эти функции (напр., школы, правительственные учреждения). Если некоторая система ориентирована на запреты, ее называют бюрократической.
Р. Акофф определил бюрократа как имеющего право сказать «нет», но не могущего сказать «да». Две причины есть для этого. Первая состоит в том, что в бюрократии «нет» не ведет к тому, что считается ошибкой, только «да» может сделать это. Поэтому лучшая стратегия, чтобы не совершить явных ошибок, — это отвергать предложения, не позволяя что-либо сделать. Бюрократ не может сказать «да», так как для этого он должен переадресовать запрос вышестоящему, чтобы не рисковать его неодобрением. Но это значит — признать ограниченность своей важности.
Вторая особенность бюрократии — установление единых нерушимых правил и ограничений, не допускающих исключений. Таким образом, бюрократы часто заняты тем, чтобы не давать другим что-то сделать. Они точно говорят, что следует делать, лишая исполнителя выбора, всякой инициативы. Нарушение инструкции — тяжкий грех; внимание и сочувствие к просителю — чужды бюрократу (так как повышает риск ошибки и последующего наказания).
Мы рассмотрели лишь несколько задач теории выбора. Критерием отбора была их частая встречаемость в практике и предстоящее использование результатов в изложении технологии решения проблем. Читатель должен знать то, что они составляют лишь незначительную часть всех вариантов практики принятия решения, неполный список которых был порожден морфологическим анализом, проведенным в начале описания данного этапа. Например, столкнувшись с необходимостью выбора в условиях неопределенности, следует идентифицировать ее тип и обратиться либо к теории игр (при неопределенности незнания), либо к теории статистических решений (при стохастической неопределенности), либо к теории нечетких множеств (при расплывчатой неопределенности). При отсутствии неопределенности последствий сделанного выбора задачи решаются методами оптимизации. По каждому из этих вариантов имеется обширная научная и учебная литература.