Прямое преобразование тепловой энергии в работу запрещается постулатом Томсона. Поэтому для этой цели используются термодинамические циклы. Термодинамические циклы это круговые процессы в термодинамике, то есть такие процессы, в которых совпадают начальные и конечные параметры, определяющие состояние рабочего тела (давление, объём, температура и энтропия). Термодинамические циклы являются моделями процессов, происходящих в реальных тепловых двигателях.
Тепловым двигателем называется устройство, способное превращать полученное количество теплоты в механическую работу. Механическая работа в тепловых двигателях производится в процессе расширения некоторого вещества, которое называется рабочим телом. В качестве рабочего тела обычно используются газообразные вещества (пары бензина, воздух, водяной пар).
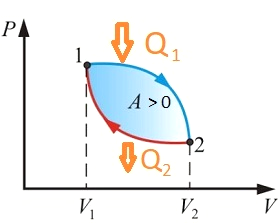
Для того, чтобы управлять состоянием рабочего тела, в тепловую машину входят нагреватель и холодильник. В каждом цикле рабочее тело забирает некоторое количество теплоты $Q_1$ у нагревателя и отдаёт количество теплоты $Q_2$ холодильнику. Работа, совершённая тепловой машиной в цикле, равна, таким образом:
$$A=Q_1-Q_2-ΔU = Q_1-Q_2.$$Изменение внутренней энергии $ΔU$ в круговом процессе равно нулю (это функция состояния), а работа не является функцией состояния, иначе суммарная работа за цикл также была бы равна нулю.
Поэтому тепловой, или, как его ещё называют, термический или термодинамический коэффициент полезного действия тепловой машины (отношение полезной работы к затраченной тепловой энергии) равен:
$$η=\frac{A}{Q_1} =\frac{Q_1-Q_2}{Q_1} =\frac{M·q_1-M·q_2}{M·q_1}=\frac{q_1-q_2}{q_1} =1-\frac{q_2}{q_1}.$$Цикл Карно. Французский инженер Сади Карно в 1824 году впервые дал теоретическое объяснение работы тепловых машин. Основное положение теории С. Карно, впоследствии получившее название принципа Карно, состоит в том, что для получения работы в тепловой машине необходимы, по крайней мере, два источника теплоты с разными температурами.
Карно предложил идеальный цикл тепловой машины, где используются два источника теплоты с постоянными температурами: источник с высокой температурой – горячий источник и источник с низкой температурой – холодный источник. Поскольку цикл идеальный, то он состоит из обратимых процессов теплообмена между рабочим телом и источниками теплоты, протекающим по двум изотермам, и двух идеальных адиабат перехода рабочего тела с одной изотермы на другую.
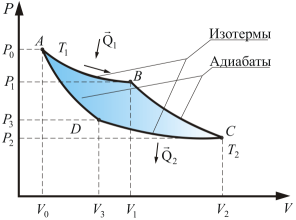
В цикле Карно горячий источник теплоты с $T_1=const$ передает теплоту рабочему телу, это обратимый процесс, поэтому рабочее тело получает теплоту $q_1$ по изотерме AB. На процессе BC рабочее тела расширяется по обратимой адиабате от $T_1$ до $T_2$. В обратимом процессе CD рабочее тело передает теплоту $q_2$ холодному источнику по изотерме $T_2=const$. На процессе DA рабочее тело сжимается по обратимой адиабате от $Т_2$ до $Т_1$.
Для цикла Карно в $T-s$ диаграмме подведенная $q_1$ и отведенная $q_2$ теплота к рабочему телу представляют площади под изотермическими процессами, которые соответствуют прямоугольникам со сторонами: для $q_1$ – с $T_1$ и $Δs$, для $q_2$ – с $T_2$ и $Δs$. Величины $q_1$ и $q_2$ определяются по формулам изотермического процесса:
$$q_1=T_1·Δs,$$ $$q_2=T_2·Δs.$$Работа цикла Карно равна разности подведенной и отведенной теплоты:
$$l_ц=q_1-q_2=(T_1-T_2)·Δs.$$В соответствии с выражением выше получить работу возможно только при наличии разности температур у горячего и холодного источников теплоты. Максимальная работа Цикла Карно теоретически была бы при $Т_2=0$ K, но в качестве холодного источника в тепловых машинах, как правило, используется окружающая среда (вода, воздух) с температурой около $300$ K. Кроме этого, достижение абсолютного нуля в природе невозможно (этот факт относится к третьему закону термодинамики). Таким образом, в цикле Карно не вся теплота $q_1$ превращается в работу, а только ее часть, Оставшаяся после получения работы теплота $q_2$, отдается холодному источнику, и при заданных $Т_1$ и $Т_2$ она не может быть использована для получения работы, величина $q_2$ является тепловыми потерями (тепловым сбросом) цикла.
Термический КПД цикла Карно может быть записан в виде
$$η=1-\frac{q_2}{q_1} =1-\frac{T_2·Δs}{T_1·Δs}=1-\frac{T_2}{T_1}.$$Таким образом, КПД цикла Карно будет тем больше, чем больше $T_1$ и меньше $T_2$. При $T_1=T_2$ КПД равен нулю, т.е. при наличии одного источника теплоты получение работы невозможно.
Цикл поршневого двигателя внутреннего сгорания (ДВС). Тепловые двигатели, рабочим телом которых являются газообразные продукты сгорания топлива, сжигаемого непосредственно внутри цилиндра двигателя, называются поршневыми двигателями внутреннего сгорания (ДВС).
Поршневые ДВС делятся на двухтактные, у которых один рабочий ход приходится на два хода поршня, и четырехтактные с одним рабочим ходом на четыре хода поршня. Кроме того, поршневые ДВС подразделяются на двигатели с подводом теплоты при постоянном объеме (быстрого сгорания), двигатели с подводом теплоты при постоянном давлении (постепенного сгорания) и двигатели, работающие по смешанному циклу.
Идеализируя рабочий цикл как двухтактных, так и четырехтактных карбюраторных двигателей внутреннего сгорания, получают термодинамический цикл, называемый часто циклом Отто. В этом цикле процесс сжатия рабочей смеси происходит по адиабате 1-2. Изохора 2-3 соответствует горению топлива, воспламененного от электрической искры, и подводу теплоты $q_1$. Рабочий ход, осуществляемый при адиабатном расширении продуктов сгорания, изображен линией 3-4. Отвод теплоты $q_2$. осуществляется по изохоре 4-1, соответствующей в четырехтактных двигателях выпуску газов и всасыванию новой порции рабочей смеси, а в двухтактных – выпуску и продувке цилиндра.
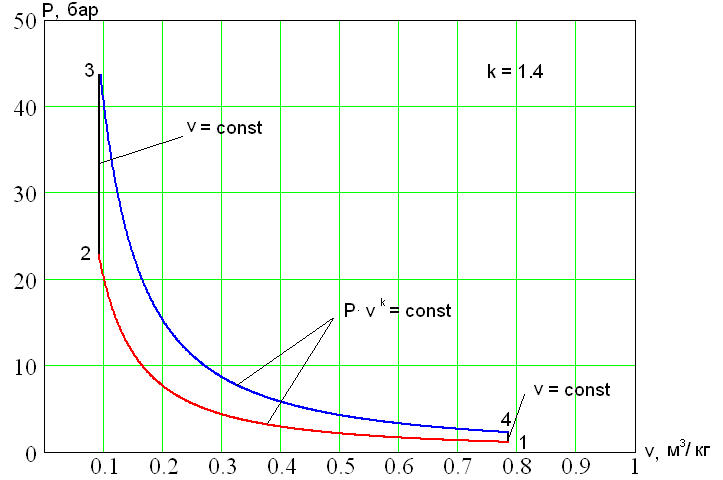
Термический КПД рассматриваемого цикла вычисляется следующим образом:
$$η_t=1-\frac{q_2}{q_1} =1-\frac{c_v·(T_4-T_1)}{c_v·(T_3-T_2)}=1-\frac{T_4-T_1}{T_3-T_2}=1 - \frac{ \frac{T_4}{T_1} - 1 }{ \frac{T_3}{T_2} - 1 } · \frac{T_1}{T_2}.$$Сравнивая адиабаты 1-2 и 3-4, можно показать, что:
$$\frac{T_4}{T_1} =\frac{T_3}{T_2}.$$и, следовательно получим:
$$η_t=1-\frac{T_1}{T_2}.$$Отношение всего объема цилиндра $v_1$ к объему камеры сгорания $v_2$ называется степенью сжатия $ε$:
$$ε=\frac{v_1}{v_2}.$$и является одной из основных конструктивных характеристик поршневого ДВС.
Учитывая, что для адиабаты 1-2 между $v$ и $T$ существует связь:
$$T_1·v_1^{k-1}= T_2·v_2^{k-1},$$окончательно имеем:
$$η_t=1-\frac{1}{ε^{k-1}}.$$Из этого выражения видно, что термический КПД двигателей, работающих по циклу Отто, зависит только от степени сжатия $ε$, и с увеличением $ε$ $η_t$ возрастает. Понятно, что температура в конце сжатия $T_2$ не должна достигать температуры самовоспламенения горючей смеси. Поэтому степень сжатия в реальных двигателях такого типа составляет порядка $7-10$ или несколько больше, в зависимости от антидетонационных свойств применяемого топлива.
Степень сжатия в цикле ДВС может быть повышена, если сжимать не горючую смесь, а воздух, и затем получив высокое давление и температуру, обеспечить самовоспламенение распыленного в цилиндре топлива. В этом случае процесс горения затягивается, и двигатели такого типа характеризуются постепенным (или медленным) сгоранием топлива при постоянном давлении. Идеализированный цикл такого двигателя внутреннего сгорания называется циклом Дизеля. Рабочее тело (воздух) сжимается по адиабате 1-2, а изобарный процесс 2-3 соответствует процессу горения топлива, т.е. подводу теплоты $q_1$. Рабочий ход выражен адиабатным расширением продуктов сгорания 3-4. Наконец, изохора 4-1 характеризует отвод теплоты $q_2$, заменяя для четырехтактных двигателей выпуск продуктов сгорания, а для двухтактных выпуск и продувку цилиндра.
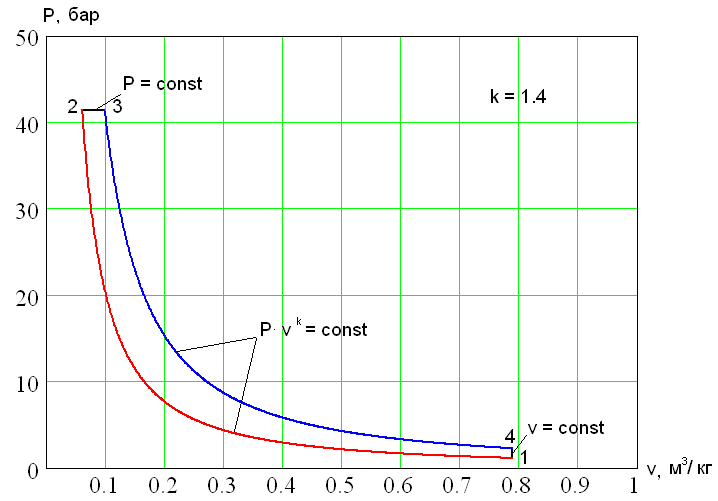
Формула для расчета термического КПД в этом случае принимает вид:
$$η_t=1-\frac{q_2}{q_1}=1-\frac{c_v·(T_4-T_1)}{c_p·(T_3-T_2)}=1-\frac{T_4-T_1}{k·(T_3-T_2)}=1-\frac{ \frac{T_4}{T_1} - 1 }{ k·\frac{T_3}{T_2} - 1 } ·\frac{T_1}{T_2}.$$Кроме степени сжатия $ε$, у цикла Дизеля имеется еще одна характеристика – степень предварительного расширения:
$$ρ=\frac{v_3}{v_2}.$$Для изобары 2-3 можно записать $\frac{v_3}{v_2}=\frac{T_3}{T_2}$. Рассматривая изохору 4-1 и учитывая $p_4·v_4^k=p_3·v_3^k$, $p_1·v_1^k=p_2·v_2^k$ и $v_4=v_1$, получаем:
$$\frac{T_4}{T_1}=\frac{p_4}{p_1}=\frac{p_4·v_4^k}{p_1·v_1^k}=\frac{p_3·v_3^k}{p_2·v_2^k}=ρ^k.$$Окончательно, с учетом соотношения $T_1·v_1^{k-1}=T_2·v_2^{k-1}$, формула для расчета термического КПД цикла Дизеля имеет вид:
$$η_t=1-\frac{ρ^k-1}{k·(ρ-1)}·\frac{1}{ε^{k-1}}.$$Это выражение показывает, что основным фактором, определяющим экономичность двигателей, работающих по циклу Дизеля, также является степень сжатия $ε$, с увеличением которой термический КПД цикла возрастает. Нижний предел для $ε$ обусловлен необходимостью получения в конце сжатия температуры воздуха, значительно превышающей температуру самовоспламенения топлива. Верхний предел $ε$ (до $20$) ограничен допустимым давлением в цилиндре, превышение которого приводит к утяжелению конструкции двигателя и увеличению потерь на трение. Повышение степени предварительного расширения $ρ$ вызывает снижение термического КПД цикла. Отсюда следует, что с увеличением нагрузки и удлинением процесса горения топлива экономичность двигателя уменьшается. Это следует учитывать, наряду с другими обстоятельствами, при определении оптимального режима работы двигателя.
Цикл Тринклера или цикл со смешанным подводом теплоты, по которому работают современные бескомпрессорные дизели, осуществляется по следующей схеме. Адиабата 1-2 соответствует сжатию в цилиндре воздуха до температуры, превышающей температуру самовоспламенения топлива, впрыскиваемого в цилиндр, а изобара 3-4 изображает процесс горения остальной части топлива по мере поступления его из форсунки. Расширение продуктов сгорания происходит по адиабате 4-5, а изохора 5-1 соответствует выпуску отработавших газов в атмосферу.
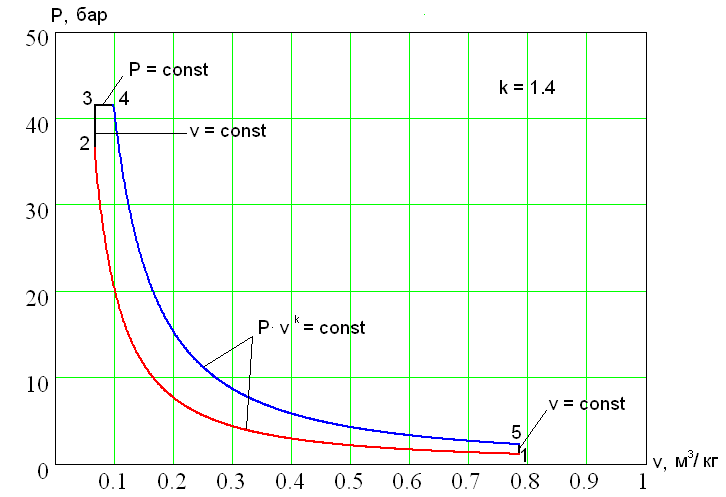
Таким образом, теплота $q_1$ подводится в двух процессах 2-3 и 3-4:
$$q_1=q_1'+q_2''.$$Приведем без вывода выражение для термического КПД цикла со смешанным подводом теплоты:
$$η_t=1-\frac{λ·ρ^k-1}{(λ-1)+k·λ·(ρ-1)}·\frac{1}{ε^{k-1}}.$$Параметр $λ$ называется степенью повышения давления и рассчитывается так:
$$λ=\frac{p_3}{p_2}.$$В двигателях, работающих по циклу Тринклера, распыл топлива производится механическим топливным насосом высокого давления, а воздушный компрессор, применяемый в двигателе Дизеля, отсутствует. Степень сжатия $ε$ в рассматриваемом цикле может достигать $18$ и более.
Легко показать, что математическое выражение термического КПД цикла со смешанным подводом теплоты является общим для циклов поршневых ДВС.
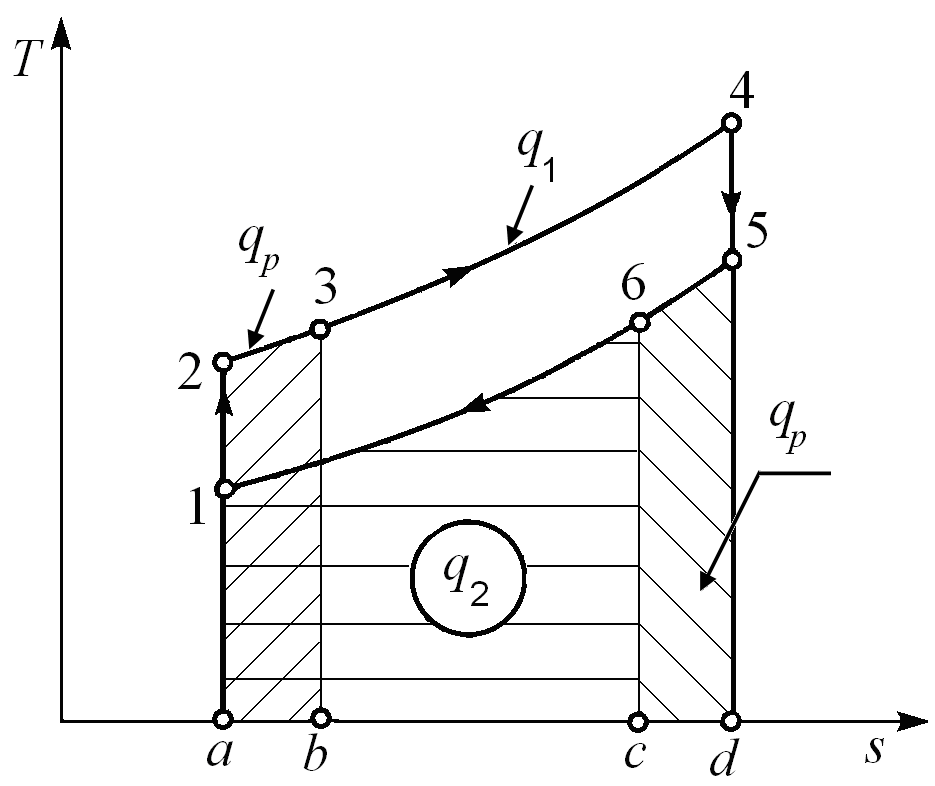
Сравнение эффективности рассмотренных циклов проведем на $T-s$ диаграмме, предположив, что в каждом из них достигается одинаковая максимальная температура $T_3$.
Одинаковы и количества отведенной теплоты $q_2$ в каждом цикле (площадь 14аb). При таких условиях теплота цикла $q_ц$, равная полезной работе цикла $l_ц$, будет наибольшей для цикла Дизеля 12”34 и наименьшей для цикла Отто 1234. Цикл Тринклера 12’3’34 занимает промежуточное положение.
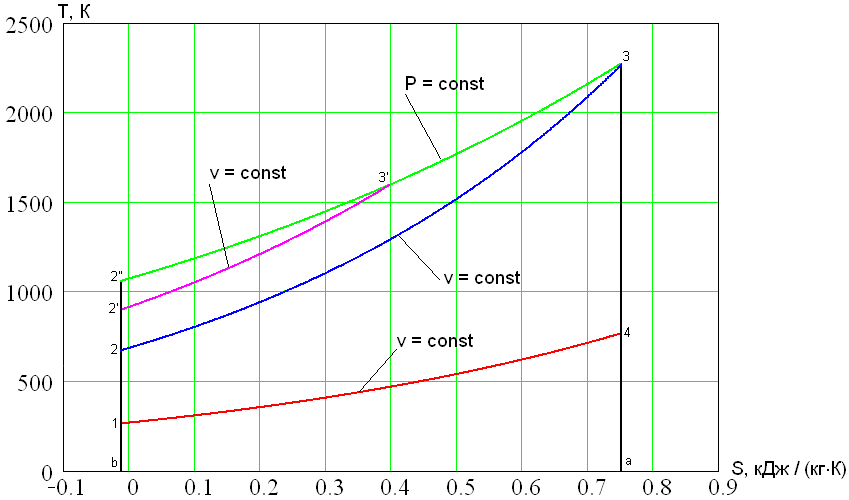
Таким образом, термический КПД, характеризующий степень термодинамического совершенства цикла, будет наибольшим для цикла Дизеля с подводом теплоты при постоянном давлении и наименьшим для цикла Отто с подводом теплоты при постоянном объеме.
Цикл двигателя Стирлинга представляет собой цикл газового двигателя поршневого типа с внешним подводом теплоты, которая получается в результате сгорания твердых, жидких, газообразных топлив. Внешний подвод теплоты осуществляется через теплопроводящую стенку. Рабочее тело (водород, гелий, аргон, углекислый газ) находится в замкнутом пространстве и во время работы не заменяется.
В общем виде схема работы устройства выглядит следующим образом: в нижней части двигателя рабочее вещество (например, воздух) нагревается и, увеличиваясь в объеме, выталкивает поршень вверх. Горячий воздух проникает в верхнюю часть мотора, где охлаждается радиатором. Давление рабочего тела снижается, поршень опускается для следующего цикла. При этом система герметична и рабочее вещество не расходуется, а только перемещается внутри цилиндра.
Существует несколько вариантов конструкции силовых агрегатов, использующих принцип Стирлинга. Например двигатель стирлинга модификации «Альфа» состоит из двух раздельных силовых поршней (горячего и холодного), каждый из которых находится в своем цилиндре. К цилиндру с горячим поршнем подводится тепло, а холодный цилиндр расположен в охлаждающем теплообменнике.
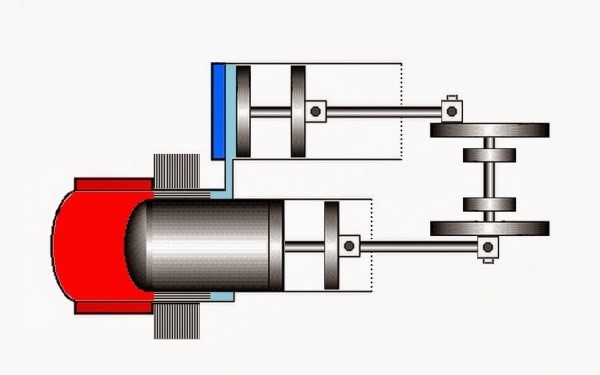
Идеальный цикл Стирлинга состоит из четырех процессов. В процессе 3 холодное рабочее тело сжимается в изотермическом процессе $T_2=const$ при интенсивном отводе теплоты $q_2''$. В процессе 4 поршень-вытеснитель перемещает рабочее тело из холодной полости в горячую, так что $v=const$ (изохорный процесс), а температура увеличивается от $T_2$ до $T_1$ при подводе теплоты $q_1'$.
В изотермическом процессе расширения 1 $T_1=const$ к рабочему телу подводится теплота $q_1''$. Затем в процессе 2 поршень-вытеснитель, перемещаясь в обратном направлении, выталкивает рабочее тело из горячей полости в холодную ($v=const$) с отводом теплоты $q_2'$. Отличительной особенностью цикла Стирлинга является то, что рабочее тело, перемещаясь из холодной полости в горячую и обратно через регенератор, то воспринимает теплоту от рабочего тела, то, охлаждаясь, отдает теплоту рабочему телу.
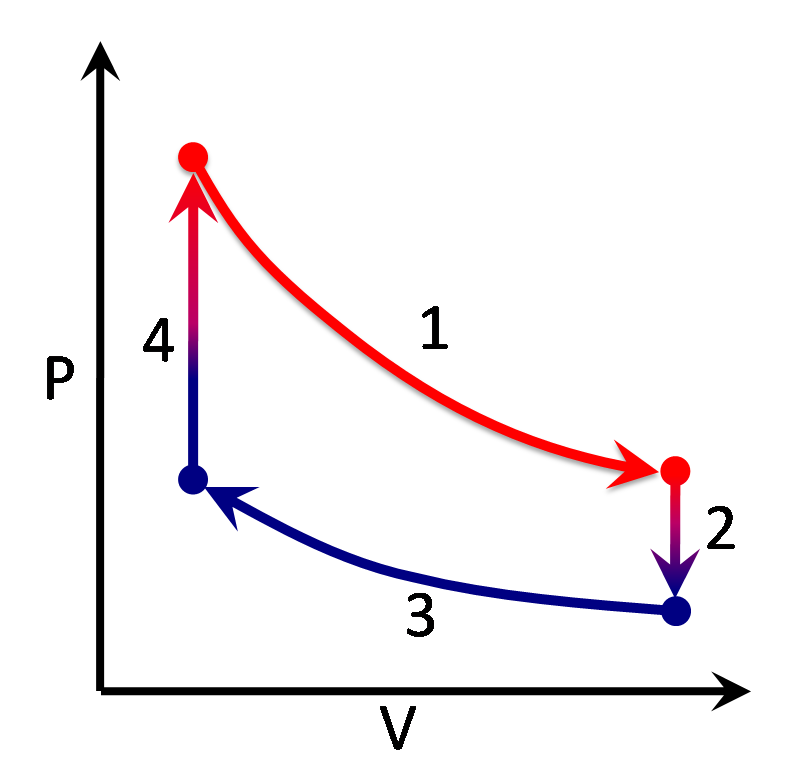
Работа в цикле Стирлинга представляет собой разность работы, полученной в процессе изотермического расширения (подвод теплоты $q_1''$), и работы, затраченной в процессе изотермического сжатия с отводом теплоты $q_2''$:
$$l_ц=q_1''-q_2''.$$Термический КПД цикла:
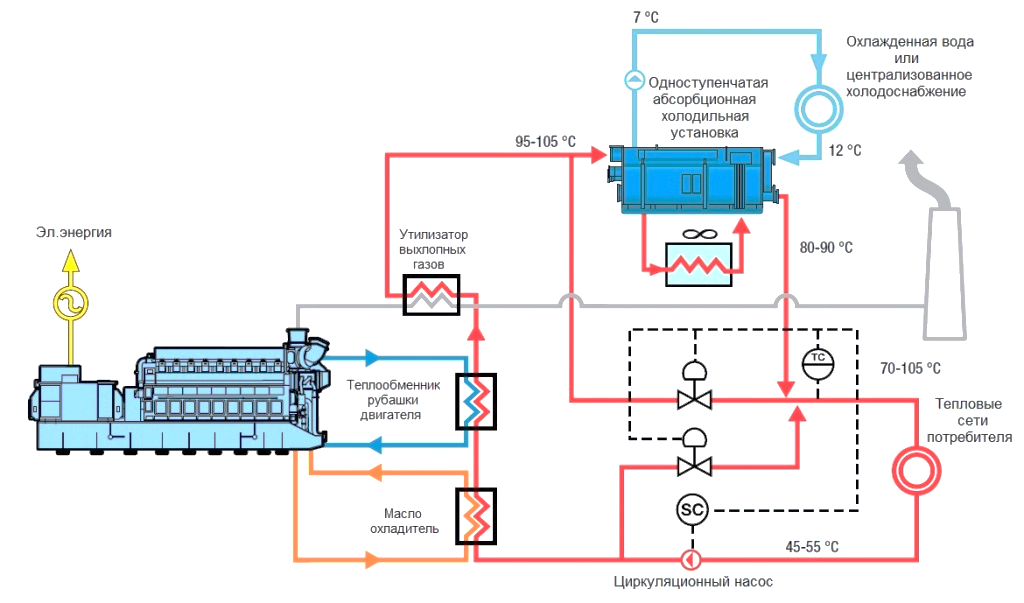
$$η_t=\frac{q_1''-q_2''}{q_1'-q_1''}.$$Дизельная электростанция как правило, объединяет в себе генератор переменного тока и двигатель внутреннего сгорания, а также систему контроля и управления установкой. Такие электростанции и установки применяются в качестве основных, резервных или аварийных источников электроэнергии для потребителей одно- или трёхфазного переменного тока.
Цикл газотурбинной установки. Одним из основных недостатков поршневых двигателей является невозможность достижения больших мощностей в одном агрегате, что сужает нишу возможного использования ДВС поршневого типа. Это связано, прежде всего с наличием кривошипно-шатунного механизма, предназначенного для преобразования возвратно-поступательного движения поршня во вращательное движение коленчатого вала. Периодичность производства рабочего хода поршня неизбежно вызывает неравномерность работы конструкции и требует наличие маховика, что заметно увеличивает удельный вес двигателя – отношение веса двигателя к вырабатываемой им мощности. Этих недостатков лишены двигатели внутреннего сгорания газотурбинного типа, к числу которых относятся воздушно-реактивные двигатели.
В газотурбинных установках подвод теплоты к рабочему телу может осуществляться при постоянном давлении (цикл Брайтона) или при постоянном объеме (цикл Гемфри).
Цикл Брайтона. Принципиальная схема газотурбинной установки со сгоранием при постоянном давлении содержит в себе все основные элементы, присущие турбокомпрессорному воздушно-реактивному двигателю. Газотурбинный двигатель состоит из размещенных на одном валу турбины, компрессора, топливного насоса и потребителя мощности. В схему входит также камера сгорания, выхлопное сопло или патрубок отвода отработавших газов и свеча зажигания.
Турбина приводит во вращение компрессор, в котором сжимается воздух, поступающий из окружающей среды. Процесс сжатия предполагается протекающим по адиабате 1-2. Сжатый воздух подается в камеру сгорания, куда насосом из топливной емкости прокачивается топливо. Тщательно перемешенная смесь в камере сгорания воспламеняется свечой зажигания, и при постоянном давлении реализуется процесс сжигания топлива. В результате протекания экзотермической реакции возрастает энтальпия продуктов сгорания – газа. Высокоэнтальпийный поток газа поступает на турбину расширяется в ней по адиабате 3-4. В процессе расширения газа на турбине генерируется мощность, снимаемая частично приводом полезной мощности (электрогенератором), частично она расходуется на привод компрессора, насоса и других агрегатов установки.
Термодинамическая эффективность теплосилового цикла оценивается термическим коэффициентом полезного действия:
$$η_t=1-\frac{1}{ε^{k-1}} =1-\frac{1}{ λ^{\frac{k-1}{k}} },$$где $ε=\frac{v_1}{v_2}$ – степень сжатия, а $λ=\frac{p_2}{p_1}$ – степень повышения давления.
Энергетический кризис, связанный с истощением запасов ископаемых энергоресурсов в виде органического топлива (газ, нефть, уголь и т. д.), делает необходимостью бережное отношение к его использованию. Вместе с тем, температура газа, покидающего турбину, еще достаточно велика и поэтому целесообразно частично вернуть избыточную по отношению к окружающей среде энергию уходящих газов в форме тепла в цикл. Обычно такой процесс называют регенерацией, суть которой состоит в полезном использовании вторичных энергоресурсов.
Отличие регенеративной газотурбинной установки от рассмотренной ранее состоит во введением дополнительного конструктивного узла в виде теплообменника регенератора, в котором тепло от уходящих газов передается к газу, сжатому компрессоре установки.
По условиям организации цикла не все избыточное тепло уходящих газов может быть передано воздуху, сжатому в компрессоре. Тогда коэффициент полезного действия можно определить:
$$η_t=1-\frac{q_2}{q_1} =\frac{ (T_5-T_1)-(T_3-T_2) }{T_4-T_2}.$$Цикл Гемфри. Газотурбинная установка со сгоранием при $v=const$ в случае, если предельные давления одинаковы и подведенные теплоты равны, будут иметь несколько большую эффективность по сравнению с изобарным циклом. Это связано с тем, что при отмеченных условиях сравнения в цикле с $v=const$ по сравнению с циклом $p=const$ отводимая теплота будет несколько меньше, чем в цикле со сгоранием при $p=const$. Это видно из сравнения циклов, построенных в $T-s$ диаграмме.
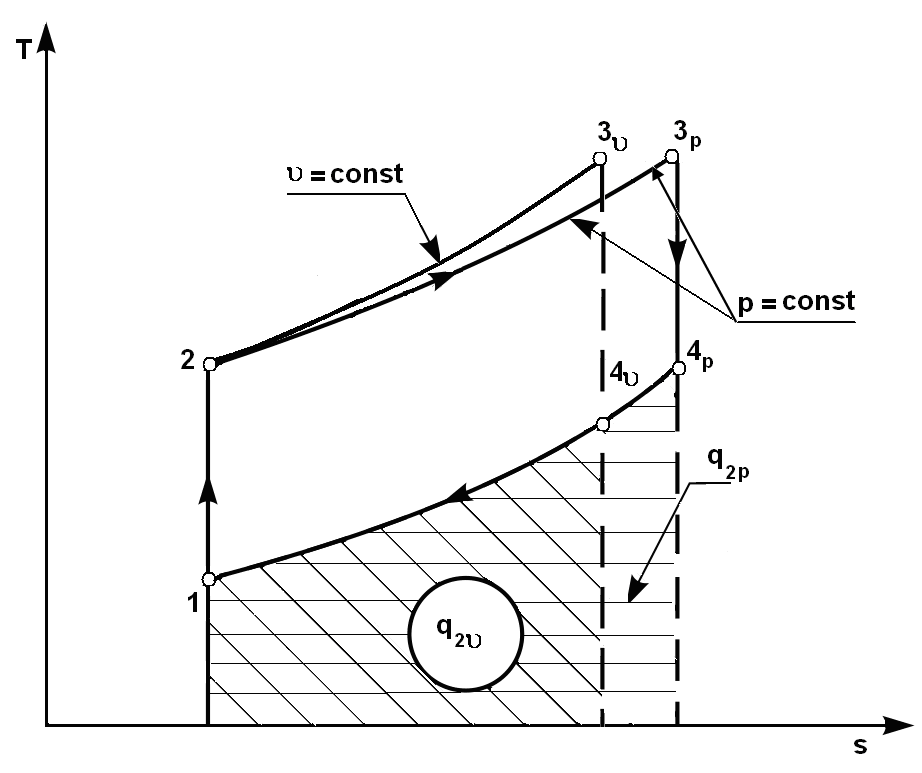
Однако в конструкторском отношении газотурбинная установка с подводом тепла при $v=const$ заметно сложнее. Турбина приводит во вращение сидящие с ней на одном валу компрессор, насос и потребитель выработанной установкой механической энергии, обычно в виде трехфазного электрогенератора. Одновременно в камеру сгорания поступает воздух, сжатый в компрессоре, и топливо подаваемое насосом. В камере сгорания при закрытых клапанах, свечой зажигания осуществляется воспламенение топлива. Сгорание топлива происходит при закрытых клапанах, т.е. при постоянном объеме. В конце процесса сгорания при достижении заданного давления открываются выпускные клапаны и рабочее тело – продукты сгорания в виде высокоэнтальпийного потока – поступает на лопатки соплового аппарата, а затем рабочего колеса, на которых энтальпия рабочего тела срабатывается, превращаясь в механическую энергию, воспринимаемую приводами. Отработавшие продукты сгорания – газы отводятся из двигателя через выхлопной патрубок.
Коэффициент полезного действия такого цикла определяется и соотношения:
$$η_t=1-\frac{k}{ε^{k-1}}·\frac{λ^{\frac{1}{k}}-1}{λ-1}.$$где $λ=\frac{p_3}{p_2}$ – степень повышения давления.
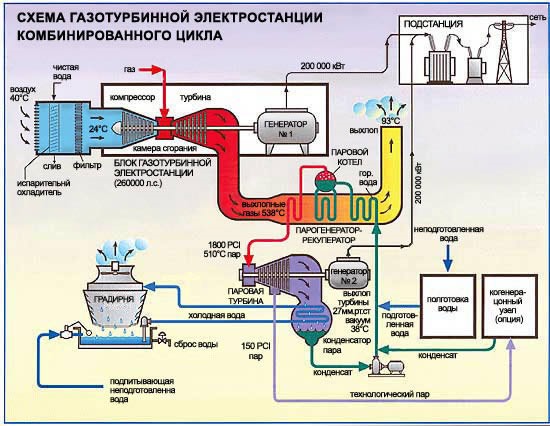
Парогазовая установка – электрогенерирующая станция, служащая для производства электроэнергии. Парогазовая установка содержит два отдельных двигателя: паросиловой и газотурбинный. В газотурбинной установке турбину вращают газообразные продукты сгорания топлива. Топливом может служить как природный газ, так и продукты нефтяной промышленности (дизельное топливо). На одном валу с турбиной находится генератор, который за счет вращения ротора вырабатывает электрический ток. Проходя через газовую турбину, продукты сгорания отдают лишь часть своей энергии и на выходе из неё, когда их давление уже близко к наружному и работа не может быть ими совершена, все ещё имеют высокую температуру. С выхода газовой турбины продукты сгорания попадают в паросиловую установку, в котел-утилизатор, где нагревают воду и образующийся водяной пар. Температура продуктов сгорания достаточна для того, чтобы довести пар до состояния, необходимого для использования в паровой турбине (температура дымовых газов около $500$ °C позволяет получать перегретый пар при давлении около $100$ атмосфер). Паровая турбина приводит в действие второй электрогенератор.