Компрессорами называют машины, предназначенные для сжатия воздуха, а также других газов и паров. Широко применяемые в технике компрессоры делятся на лопаточные и объемные. В лопаточных компрессорах (центробежных и осевых) рабочее тело в результате вращения ротора разгоняется до значительных скоростей, а затем кинетическая энергия потока превращается в потенциальную энергию давления. При этом давление в вентиляторах возрастает до $0.01$ МПа, в воздуходувных машинах – до $0.3$ МПа. В объемных компрессорах (поршневых и ротационных) газ сжимается за счет уменьшения замкнутого объема, в котором он находится.
Хотя компрессоры различных типов отличаются принципом сжатия газа и имеют значительные конструктивные различия, сущность термодинамических процессов в них одинакова.
Рассмотрим работу идеального поршневого одноступенчатого компрессора и процессы, происходящие при получении $1$ кг сжатого газа с заданным давлением $p_2$ на $p-v$ и $T-s$ диаграммах.
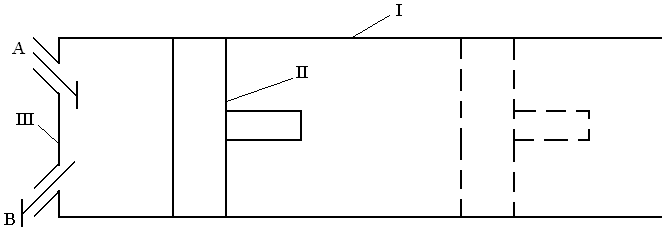
Линия 6-1 изображает процесс всасывания газа в цилиндр I в результате перемещения поршня II вправо от крышки цилиндра III, в которой находятся впускной клапан А и выпускной клапан В. Давление газа повышается при обратном ходе поршня (линия 1-2) до значения $p_2$ в момент открытия выпускного клапана В. Продолжая движение влево, поршень выталкивает сжатый газ в резервуар (линия 2-5) и выпускной клапан закрывается. Затем происходит открывание впускного клапана А и заполнение цилиндра новой порцией газа.
Процесс повышения давления от $p_1$ до $p_2$ может происходить по адиабате 1-3 при отсутствии теплообмена между рабочим телом и окружающей средой.
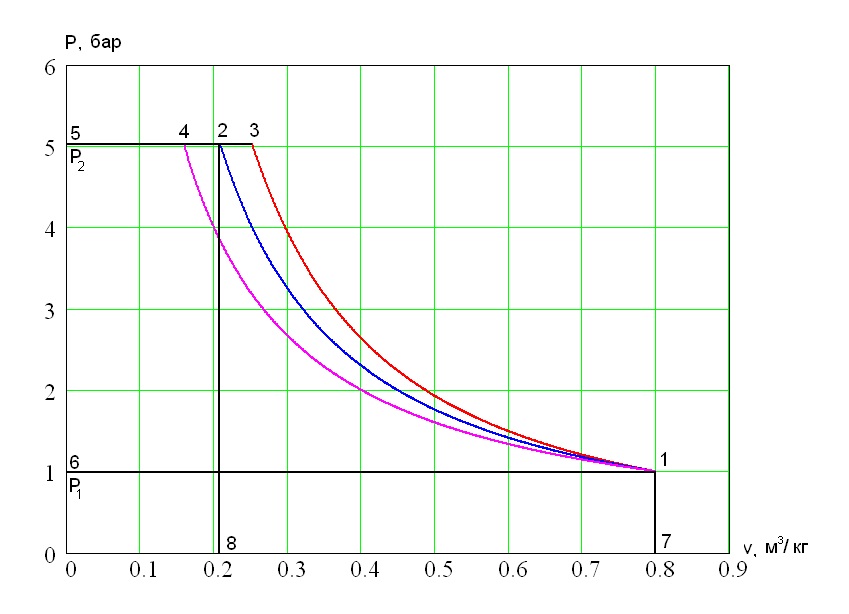
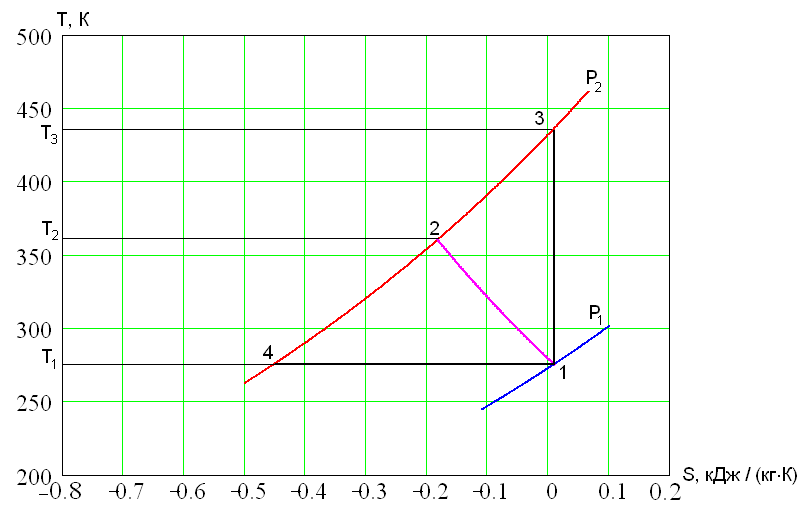
Если отвести от рабочего тела количество теплоты, эквивалентное работе, затраченной на сжатие от $p_1$ до $p_2$, то температура останется постоянной и процесс 1-4 будет изотермическим. В реальных условиях вода, циркулирующая в рубашке компрессора или внешний принудительный обдув цилиндров, обеспечивают охлаждение сжимаемого газа, отводя лишь часть теплоты, и процесс 1-2 является политропным с показателем $1 < n < k$ (у реальных машин $n=1.15÷1.35$).
Полная теоретическая работа $l_0$, затрачиваемая на получение одного кг газа с давлением $p_2$, складывается из работ сжатия $l_{сж}$, выталкивания $l_{выт}$ и всасывания $l_{вс}$:
$$l_0=l_{сж}+l_{выт}-l_{вс}.$$Работа $l_{сж}$ изображается площадью 12871, работа $l_{выт}$ − площадью 25082 и работа $l_{вс}$ − площадью 16071. Работа всасывания $l_{вс}$ имеет противоположный знак по отношению к работам $l_{сж}$ и $l_{выт}$. Суммирование указанных площадей дает теоретическую работу компрессора $l_0$.
Работа сжатия в процессе 1-2 в общем случае:
$$l_{сж}=\intop_{v_1}^{v_2} p \mathrm{d}v.$$Для адиабатного сжатия идеального газа:
$$l_{сж}^{ад}=\frac{1}{k-1}·(p_2·v_2-p_1·v_1).$$Для изотермического сжатия:
$$l_{сж}^{т}=p_1·v_1·\ln\left(\frac{p_2}{p_1} \right).$$Для политропного сжатия:
$$l_{сж}^{ад}=\frac{1}{n-1}·(p_2·v_2-p_1·v_1 ).$$Работу всасывания и выталкивания вычисляют следующим образом:
$$l_{вс}=p_1·v_1.$$ $$l_{выт}=p_2·v_2.$$Окончательно получаем для политропного сжатия:
$$l_0=\frac{1}{n-1}·(p_2·v_2-p_1·v_1)+p_2·v_2-p_1·v_1=\frac{n}{n-1}·(p_2·v_2-p_1·v_1 ).$$Преобразуя можно получить:
$$l_0=\frac{n}{n-1}·p_1·v_1·\left(\left(\frac{p_2}{p_1}\right)^{\frac{n-1}{n}}-1\right).$$Полную теоретическую работу также можно найти из соотношения:
$$l_0=\intop_{p_1}^{p_2} v\mathrm{d}p.$$Количество отводимой теплоты при сжатии в цилиндре определяется по формуле:
$$q=c_n·(T_2-T_1 )=c_v·\frac{n-k}{n-1}·(T_2-T_1).$$При адиабатном сжатии работа будет наибольшей. По мере увеличения количества отводимой теплоты она уменьшается и при изотермическом сжатии будет наименьшей. Отметим также, что в конце адиабатного сжатия температура может достигнуть высоких значений. Это приводит к ухудшению качества смазки деталей цилиндропоршневой группы и соответственно к повышенному износу в процессе эксплуатации. Применение же охлаждения стенок цилиндров водой или воздухом окружающей среды кроме уменьшения работы сжатия создает еще и более благоприятные условия работы деталей цилиндро-поршневой группы.
В реальных компрессорах из конструктивных соображений предусматривается некоторый объем $v_0$, представляющий собой пространство между поршнем, находящимся в верхней мертвой точке и поверхностью крышки цилиндра. Этот объем с термодинамической точки зрения принято называть “вредным” пространством. Оставшийся в этом объеме сжатый газ при обратном ходе поршня в цилиндре компрессора расширяется по политропному процессу (линия 3-4).
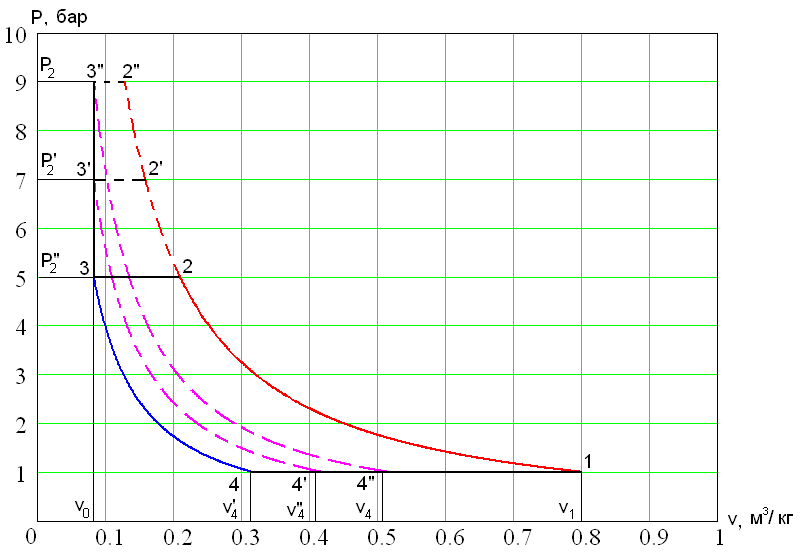
Всасывающий клапан откроется лишь после прохождения части хода поршня, когда давление в цилиндре снизится до $p_1$. В связи с этим объем поступившего газа будет меньше $v_1-v_0$ и производительность компрессора следовательно уменьшится. При увеличении конечного давления $p_2$ до значении $p_2'$ и $p_2''$ и т.д. производительность продолжает падать, так как количество газа, остающегося в конце процесса выталкивания возрастает и для снижения давления до $p_1$, увеличивается участок хода поршня на этапе политропного расширения 3'' – 4'' При некотором конечном давлении, когда объем сжатого газа будет равен $v_0$, производительность компрессора станет равной нулю.
Из изложенного видно, что по мере повышения давления нагнетания снижается производительность компрессора, поэтому для получения высоких давлений применяют многоступенчатые компрессоры, в которых после каждой ступени газ поступает в промежуточный холодильник, где охлаждается при постоянном давлении до исходной температуры.
В идеальном трехступенчатом компрессоре осуществляются следующие процессы: всасывание газа в первую, вторую и третью ступени-линии а1, в3 и с5; выталкивание сжатого газа из первой ступени во вторую, из второй в третью и из третьей ступени в резервуар (каждый раз через промежуточные холодильники-линии 2в 4с и 6д). Отрезки линий 2-3 и 4-5 определяют изобарное охлаждение газа в холодильниках. Те же процессы представлены на $T-s$ диаграмме.
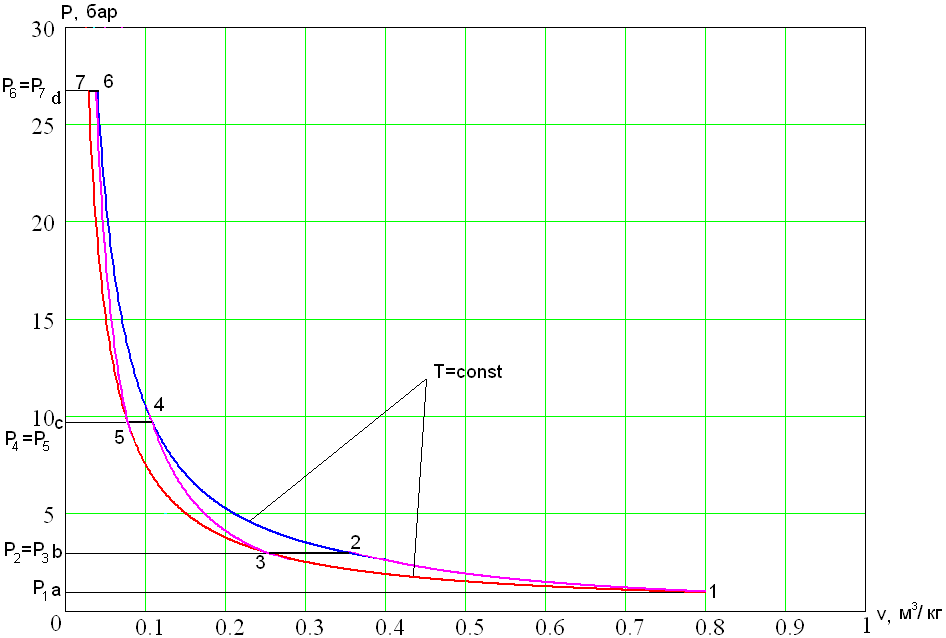
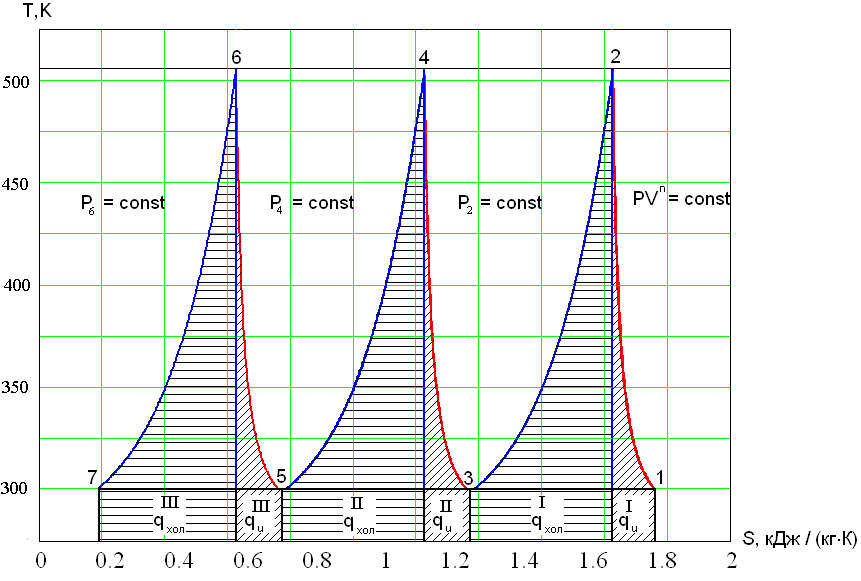
Если температура газа после каждого холодильника равна исходной ( $T_1=T_3=T_5$), конечные температуры на выходе из каждой ступени также одинаковы ($T_2=T_4=T_6$) и все процессы идут с одинаковым показателем политропы, то и степени повышения давления в ступенях $x$ будут равны между собой:
$$x=\frac{p_2}{p_1} = \frac{p_4}{p_3} = \frac{p_6}{p_5}.$$Учитывая, что $p_2=p_3$ и $p_4=p_5$, получим:
$$x=\sqrt[3]{\frac{p_6}{p_1}}.$$В общем случае при числе ступеней $z$:
$$x=\sqrt[z]{\frac{p_{кон}}{p_{нач}}}.$$Для определения общей работы, затрачиваемой многоступенчатым компрессорам, необходимо просуммировать работы, расходуемые на сжатие газа в каждой ступени.
Для компрессора с числом ступеней $z$ значение общей затраченной работы равно:
$$l_0=z·\frac{n}{n-1}·p_1·v_1·\left(\left(\frac{p_2}{p_1}\right)^{\frac{n-1}{n}}-1\right).$$Из $p-v$ диаграммы хорошо видно, что при промежуточном охлаждении газа существенно уменьшаются затраты работы и общая картина сжатия по мере увеличения числа ступеней приближается к изотермическому процессу.
Количество теплоты, отводимой от газа в каждом холодильнике, установленном между ступенями, определяется по формуле:
$$q_{хол}=c_p·(T_2-T_1 ).$$Конечная температура сжатия в каждом цилиндре определяется из уравнения политропы:
$$T_2=T_1·\left(\frac{p_2}{p_1}\right)^{\frac{n-1}{n}}=T_1·x^{\frac{n-1}{n}}.$$Количество отводимой теплоты при сжатии в цилиндре и в холодильнике для многоступенчатого компрессора могут быть определены как площади под политропами и изобарами на $T-s$ диаграмме.