Energy
education

5. Функции

Произвольные зависимости между входными и выходными параметрами задаются при помощи функций. В формулах рабочего листа можно использовать стандартные встроенные функции, а также функции, определенные пользователем. Функции обозначаются именем функции, за которым следует один или несколько операндов, заключенных в круглые скобки. Операнды функций называются аргументами, и каждый аргумент определяется выражением. Результат функции рассчитывается посредством применения действия функции к аргументам.

Пользовательские функции должны быть сначала определены. Определение задается при помощи оператора присваивания. В левой части указывается имя пользовательской функции и в скобках формальные параметры – переменные, от которых она зависит. Справа от знака присваивания эти переменные должны использоваться в выражении.

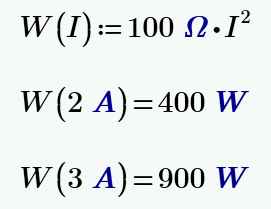
В PTC Mathcad содержится более 700 встроенных функций.

Специальные функции:

• J0, J1, Jn, Y0, Y1, Yn – функции Бесселя первого и второго рода.
• I0, I1, In, K0, K1, Kn – модифицированные (гиперболические) функции Бесселя.
• exp, log, ln, ln0 – экспоненциальные и логарифмические выражения.
• cos, cot, csc, sec, sin, sinc, tan – вычисляют стандартные тригонометрические функции. Аргументы задаются в радианах.
• acos, acot, acsc, asec, asin, atan – вычисляют обратные тригонометрические функции.
• cosh, coth, csch, sech, sinh, tanh – вычисляют гиперболические тригонометрические функции.
• acosh, acoth, acsch, asech, asinh, atanh – вычисляют обратные гиперболические функции.

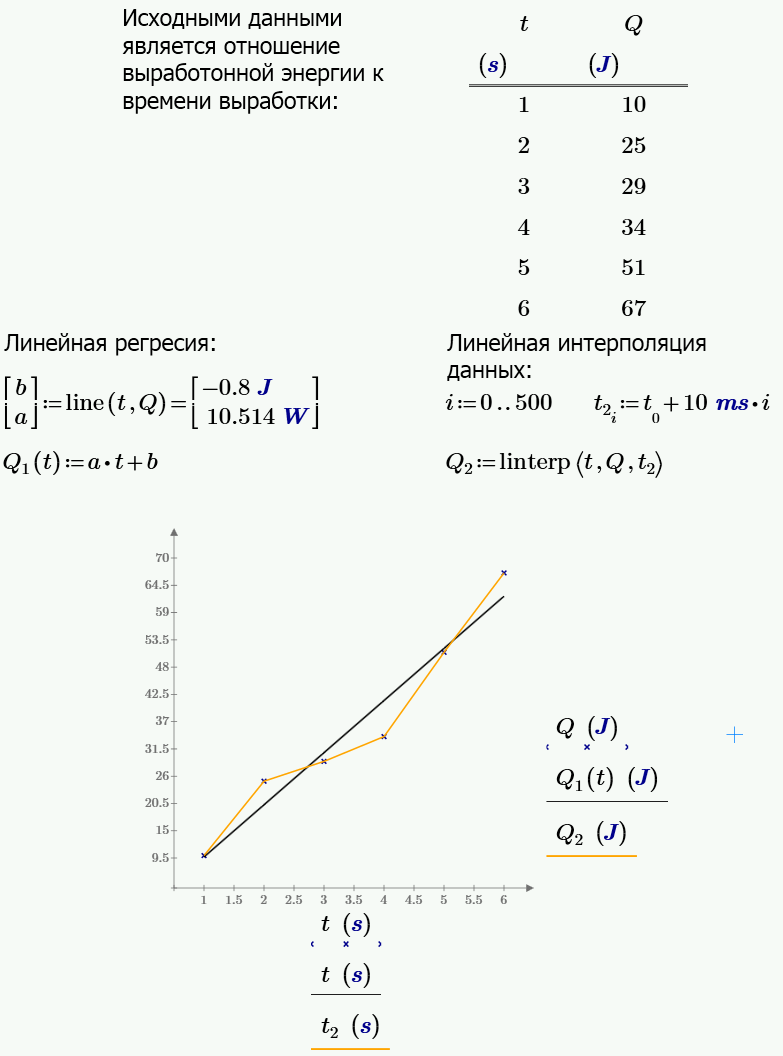
Функции анализа данных. С помощью встроенных функций анализа данных PTC Mathcad можно получать и анализировать данные, а также управлять ими. Например, при осуществлении аппроксимации кривой проводится подгонка одиночной функции по всем точкам данных методом наименьших квадратов. Этот метод отличается от интерполяции, при которой кусочные функции подгоняются по смежным точкам данных. Для дальнейшего анализа данных или определения приемлемости выбранной регрессии может понадобиться применить другие статистические функции, предназначенные для анализа данных.

Линейная и медиан-медианная регрессия

• line, slope, intercept, stderr – линейная регрессия по методу наименьших квадратов для данных и среднеквадратическая ошибка, связанная с линейной регрессией.
• medfit – медиан-медианная линейная регрессия для данных.

Полиномиальная регрессия и регрессия рациональной функции

• loess – локализованная полиномиальная регрессия.
• rationalfit, rationalfitnp – регрессия рациональной функции по методу наименьших квадратов.
• polyfit, polyfitc, polyfitstat – многомерная полиномиальная регрессия.

Нелинейная регрессия

• genfit – нелинейная регрессия по методу наименьших квадратов для произвольных функций подгонки.
• expfit – экспоненциальная регрессия по методу наименьших квадратов.
• lnfit, logfit – логарифмическая регрессия по методу наименьших квадратов.
• lgsfit – регрессия логистической кривой по методу наименьших квадратов.
• pwrfit – регрессия кривой мощности по методу наименьших квадратов.
• sinfit – синусоидальная регрессия по методу наименьших квадратов.

Интерполяция – это процесс поиска промежуточных значений в данных путем подгонки подходящих функций (обычно полиномов) кусочно через соседние точки данных. Данный метод отличается от регрессии, при которой одна функция подгоняется методом наименьших квадратов через все точки данных.

Поскольку функции интерполяции должны проходить через все точки данных, они очень чувствительны к ложным данным. Если данные содержат шумы, следует рассмотреть вариант использования функции регрессии.

• interp – интерполяция в заданной точке выходных данных функций cspline, lspline, pspline, bspline или loess.
• bspline, Spline2, Binterp, DWS – интерполяция B-сплайном с заданными пользователем узлами.
• cspline, pspline, lspline, Bicubic2D – интерполяция кубическим сплайном в одном и двух измерениях с кубическими, параболическими и линейными условиями на концах.
• linterp – линейная интерполяция.
• predict – линейный прогноз.
• polyint, polycoeff, polyinter – полиномиальная интерполяция.
• rationalint – интерполяция рациональной функцией.
• Thielecoeff, Thiele – непрерывная дробная интерполяция Тиле.

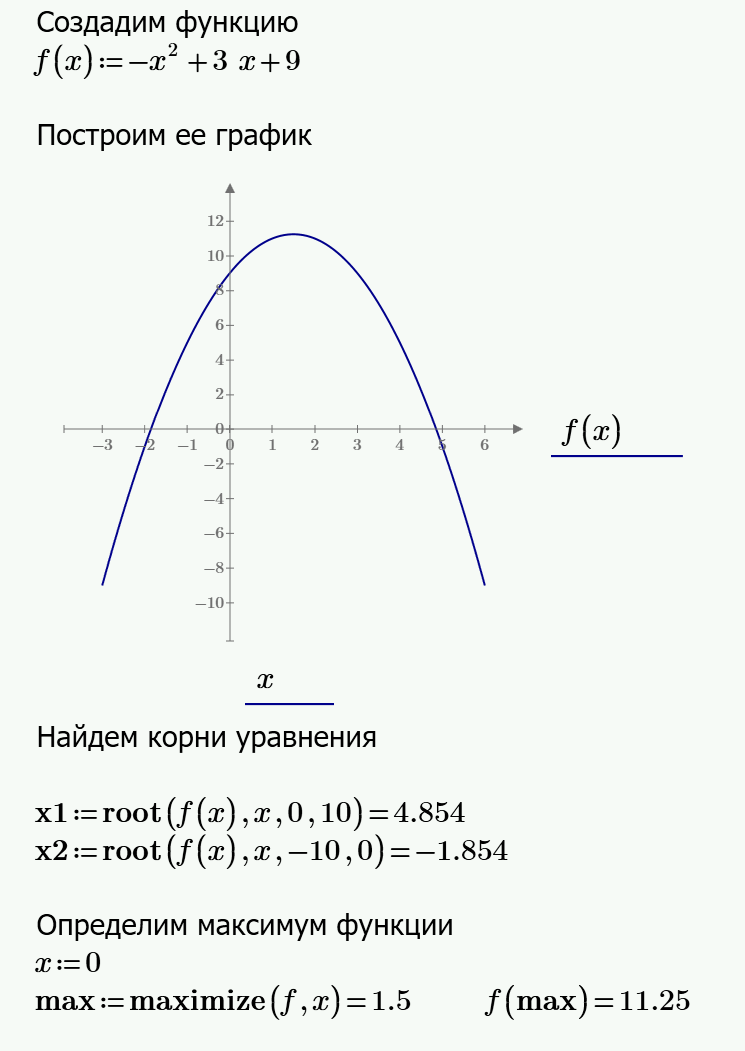
Нахождение корней уравнений. Корнем функции является значение, в котором функция равна нулю. Функция root(f(var1, var2, ...), var1, [a, b]) — возвращает значение параметра var1, при котором функция f равна нулю. Если указаны параметры a и b, функция root находит параметр var1 в интервале [a, b]. В противном случае должно быть определено начальное приближение параметра var1 перед вызовом функции root. При использовании начального приближения в функции root используется метод секущих или метод Мюллера. В случае использования интервала в качестве начального приближения корня в функции root используется метод Риддера или Брента. Чтобы решить уравнение вида f(x) = g(x), используйте выражение, подобное следующему: x0 := root(f(x) − g(x), x).

Функции оптимизации. Функции maximize(f, var1, var2, ...) и minimize(f, var1, var2, ...) возвращают такие значения всех аргументов целевой функции f, чтобы были соблюдены ограничения, заданные в блоке решения, а функция f принимала свое максимальное или минимальное значение соответственно. Для функции одной переменной решением является скаляр. Для функции нескольких переменных решением является вектор, в котором первый элемент является решением для var1, второй — для var2 и т. д. PTC Mathcad подбирает значения всех аргументов функции одновременно для минимизации погрешности. Для оптимизации функции без ограничений можно использовать функции maximize и minimize вне блока решения. PTC Mathcad игнорирует ограничения, указанные вне блоков решения.