Цель любого управления – изменить состояние объекта нужным образом (в соответствии с заданием). Теория автоматического регулирования должна ответить на вопрос: «как построить регулятор, который может управлять данным объектом так, чтобы достичь цели?» Для этого разработчику необходимо знать, как система управления будет реагировать на разные воздействия, то есть нужна модель системы: объекта, привода, датчиков, каналов связи, возмущений, шумов.
Модель – это объект, который мы используем для изучения другого объекта (оригинала).
Модель и оригинал должны быть в чем-то похожи, чтобы выводы, сделанные при изучении модели, можно было бы (с некоторой вероятностью) перенести на оригинал. Нас будут интересовать в первую очередь математические модели, выраженные в виде формул. Кроме того, в науке используются также описательные (словесные), графические, табличные и другие модели.
Любой объект взаимодействует с внешней средой с помощью входов и выходов. Входы – это возможные воздействия на объект, выходы – это те сигналы, которые можно измерить. Например, для электродвигателя входами могут быть напряжение питания и нагрузка, а выходами – частота вращения вала, температура.
Входы независимы, они «приходят» из внешней среды. При изменении информации на входе меняется внутреннее состояние объекта (так называют его изменяющиеся свойства) и, как следствие, выходы:
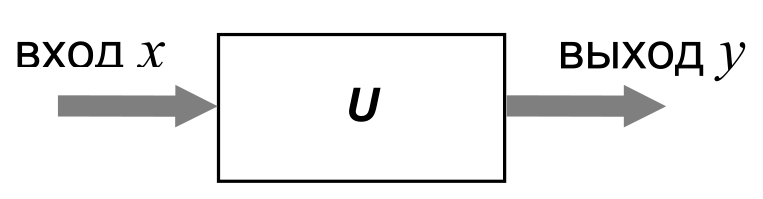
Это значит, что существует некоторое правило, по которому элемент преобразует вход $x$ в выход $y$. Это правило называется оператором. Запись $y = U[x]$ означает, что выход y получен в результате применения оператора $U$ ко входу $x$.
Построить модель – это значит найти оператор, связывающий входы и выходы. С его помощью можно предсказать реакцию объекта на любой входной сигнал.
Рассмотрим электродвигатель постоянного тока. Вход этого объекта – это напряжение питания (в вольтах), выход – частота вращения (в оборотах в секунду). Будем считать, что при напряжении 1 В частота вращения равна 1 об/сек, а при напряжении 2 В – 2 об/сек, то есть частота вращения равна по величине напряжению. Легко видеть, что действие такого оператора можно записать в виде
$$U[x]=x.$$Теперь предположим, что этот же двигатель вращает колесо и в качестве выхода объекта мы выбрали число оборотов колеса относительно начального положения (в момент $t = 0$ ). В этом случае при равномерном вращении произведение $x⋅∆t$ дает нам количество оборотов за время $∆t$ , то есть $y(t) = x⋅∆t$ (здесь запись $y(t)$ явно обозначает зависимость выхода от времени $t$). Можно ли считать, что этой формулой мы определили оператор $U$? Очевидно, что нет, потому что полученная зависимость справедлива только для постоянного входного сигнала. Если напряжение на входе $x(t)$ меняется (все равно как!), угол поворота запишется в виде интеграла
$$U[x(t)]=∫_0^t x(t)\mathrm{d} t.$$Оператор, который действует по такому правилу, называется оператором интегрирования. С помощью этого оператора можно, например, описать наполнение пустого бака водой. Если сечение бака $S$ (в м2) постоянно по всей его высоте, то уровень воды $h$ определяется как интеграл от потока воды $q$ (в м3/с), деленный на $S$:
$$h(t)=\frac{1}{S} ∫_0^t q(t)\mathrm{d} t.$$Обратный оператор – оператор дифференцирования – вычисляет производную:
$$U[x(t)]=\frac{\mathrm{d}x(t)}{\mathrm{d}t}.$$Этот оператор играет очень важную роль в описании объектов управления.
Обычно оператор дифференцирования обозначается буквой $p$. Запись $y(t) = p\ x(t)$ внешне выглядит как «умножение» оператора $p$ на сигнал $x(t)$, но на самом деле обозначает действие этого оператора, то есть дифференцирование:
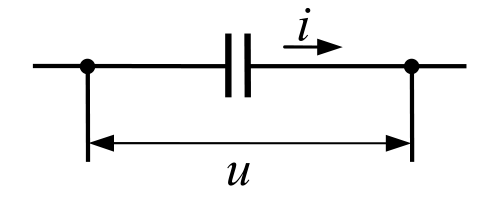
$$p\ x(t)=\frac{\mathrm{d}x(t)}{\mathrm{d}t}.$$Где встречаются такие операторы? Приведем примеры из электротехники. Например, известно, что ток $i$ (в амперах), проходящий по цепи с конденсатором, пропорционален производной от разности потенциалов $u$ (в вольтах) на его пластинах:
$$i(t)=C \frac{\mathrm{d}u(t)}{\mathrm{d}t}=C\ p\ u(t).$$Здесь $C$ – емкость конденсатора (измеряется в фарадах).
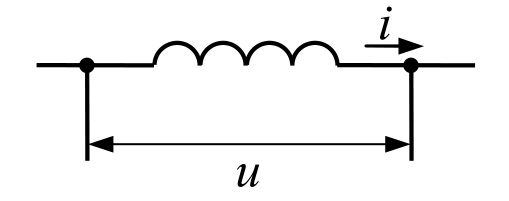
Кроме того, падение напряжения $u$ на катушке индуктивности пропорционально производной от проходящего тока $i$:
$$u(t)=L \frac{\mathrm{d}i(t)}{\mathrm{d}t}=L\ p\ i(t).$$где $L$ – индуктивность (измеряется в генри).
Оператор дифференцирования – это идеальный (физически нереализуемый) оператор, его невозможно реализовать на практике. Чтобы понять это вспомним, что при мгновенном изменении сигнала его производная (скорость возрастания) будет равна бесконечности, а никакое реальное устройство не может работать с бесконечными сигналами.
Во-первых, математические модели могут быть получены теоретически из законов физики (законы сохранения массы, энергии, импульса). Эти модели описывают внутренние связи в объекте и, как правило, наиболее точны.
Рассмотрим $RLC$-цепочку, то есть последовательное соединение резистора с сопротивлением $R$ (в омах), катушки индуктивности с индуктивностью $L$ и конденсатора с емкостью $C$.
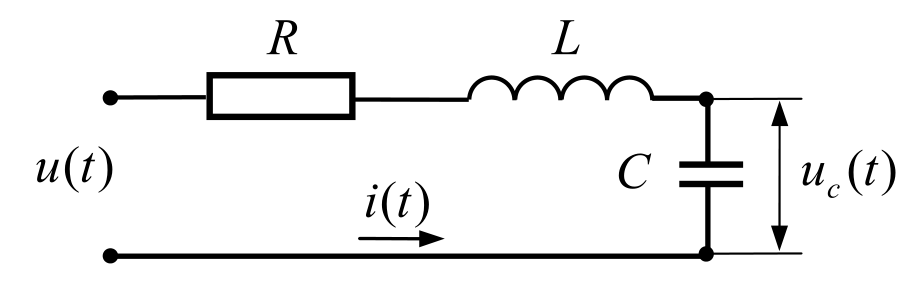
Она может быть описана с помощью двух уравнений:
$$u(t)=u_c (t)+L \frac{\mathrm{d}i(t)}{\mathrm{d}t}+R·i(t),$$ $$i(t)=C \frac{\mathrm{d}u_c (t)}{\mathrm{d}t}.$$Первое уравнение означает, что разность потенциалов на концах $RLC$-цепочки равна сумме разностей потенциалов на всех промежуточных участках. Разность потенциалов $R⋅i(t)$ на резисторе вычисляется по закону Ома. Второе уравнение описывает связь между напряжением и током для конденсатора. Вход этого объекта – напряжение $u(t)$ на концах цепочки, а выход – разность потенциалов $u_c (t)$ на пластинах конденсатора.
Второй способ – построение модели в результате наблюдения за объектом при различных входных сигналах (этим занимается теория идентификации). Объект рассматривается как «черный ящик», то есть, его внутреннее устройство неизвестно. Мы смотрим, как он реагирует на входные сигналы, и стараемся подстроить модель так, чтобы выходы модели и объекта совпадали как можно точнее при разнообразных входах.
На практике часто используется смешанный способ: структура модели (вид уравнения, связывающего вход и выход) определяется из теории, а коэффициенты находят опытным путем.
Например, общий вид уравнений движения корабля хорошо известен, однако в этих уравнениях есть коэффициенты, которые зависят от многих факторов (формы корпуса, шероховатости поверхности и т.п.), так что их крайне сложно (или невозможно) найти теоретически. В этом случае для определения неизвестных коэффициентов строят масштабные модели и испытывают их в бассейнах по специальным методикам. В авиастроении для тех же целей используют аэродинамические трубы.
Для любого объекта управления можно построить множество различных моделей, которые будут учитывать (или не учитывать) те или иные факторы. Обычно на первом этапе стараются описать объект как можно более подробно, составить детальную модель. Однако при этом будет трудно теоретически рассчитать закон управления, который отвечает заданным требованиям к системе. Даже если мы сможем его рассчитать, он может оказаться слишком сложным для реализации или очень дорогим.
С другой стороны, можно упростить модель объекта, отбросив некоторые «детали», которые кажутся разработчику маловажными. Для упрощенной модели закон управления также получается проще, и с его помощью часто можно добиться желаемого результата. Однако в этом случае нет гарантии, что он будет так же хорошо управлять полной моделью (и реальным объектом).
Обычно используется компромиссный вариант. Начинают с простых моделей, стараясь спроектировать регулятор так, чтобы он «подходил» и для сложной модели. Это свойство называют робастностью (грубостью) регулятора (или системы), оно означает нечувствительность к ошибкам моделирования. Затем проверяют работу построенного закона управления на полной модели или на реальном объекте. Если получен отрицательный результат (простой регулятор «не работает»), усложняют модель, вводя в нее дополнительные подробности.
Из математики известно, что проще всего решать линейные уравнения. С нелинейными уравнениями (квадратными, кубическими и др.) работать намного сложнее, многие типы уравнений математика пока не умеет решать аналитически.
Среди операторов самые простые – также линейные. Они обладают двумя свойствами:
Модели, которые описываются линейными операторами, называются линейными. С ними можно работать с помощью методов теории линейных систем, которая наиболее развита и позволяет точно решать большинство известных практических задач.
Однако, все модели реальных систем – нелинейные. Это легко понять хотя бы потому, что всегда есть предельно допустимое значение входного сигнала – при его превышении объект может просто выйти из строя или даже разрушиться (линейность нарушается). Методы исследования нелинейных операторов очень сложны математически, в теории нелинейных систем точные решения известны только для достаточно узкого круга задач.
Поэтому, чаще всего сначала проводят линеаризацию нелинейной модели объекта (привода), то есть строят приближенную линейную модель. Затем на основе этой модели проектируют закон управления, применяя точные методы теории линейных систем. Наконец, проверяют полученный регулятор с помощью компьютерного моделирования на полной нелинейной модели.
Нужно отметить, что если объект или привод имеют так называемую «существенную» нелинейность, этот подход может не сработать. Тогда приходится использовать методы нелинейной теории, а также компьютерное моделирование. Моделирование стало очень популярным в последнее время, поскольку появились мощные компьютерные программы для проведения вычислительных экспериментов, и можно проверить поведение системы при разнообразных допустимых входных сигналах.
Таким образом, в классификацию систем управления нужно добавить еще одно деление, может быть, самое существенное – системы бывают линейные и нелинейные. В линейных системах все звенья описываются линейными операторами, и это значительно упрощает работу с ними.
В теории управления лучше всего разработаны методы исследования линейных систем, однако строго линейных систем в окружающем нас мире не существует. Поэтому для того, чтобы эти методы можно было применить на практике, нужно выполнить линеаризацию – построить приближенную линейную модель на основе более реалистичной нелинейной модели объекта.
Представим себе бак с водой. В нижней части бака просверлено отверстие, через которое вытекает вода. Площадь сечения бака обозначим через $S$, а площадь сечения отверстия – через $S_0$.
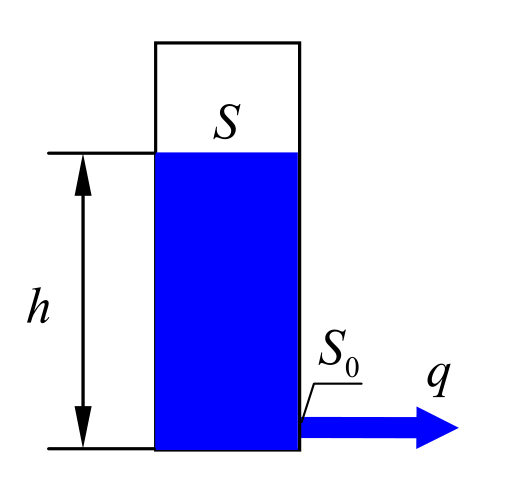
Построим модель, которая связывает уровень воды в баке $h$ (в метрах) и расход вытекающей воды $q$ (в м3/с). Эту связь можно найти с помощью закона Бернулли, который в данном случае принимает вид
$$ρ·g·h=\frac{ρ·v^2}{2}.$$Здесь $ρ$ – плотность жидкости, кг/м3, $g ≈ 9.81$ м/с2 – ускорение свободного падения, $v$ – скорость вытекания жидкости, м/с. Отсюда получаем $v = \sqrt{2·g·h}$ . Учитывая, что расход воды вычисляется как $q = S_0·v$, находим
$$q=α\sqrt{h}.$$где $α=S_0 \sqrt{2g}$ – постоянная величина. Это статическая модель, потому что она не содержит производных, характеризующих изменение сигналов во времени. Статическая модель описывает установившееся состояние (статический режим), когда в баке поддерживается постоянный уровень воды и поток вытекающей воды тоже постоянный.
Очевидно, что модель – нелинейная, поскольку содержит $\sqrt{h}$. Линеаризовать ее – значит приближенно заменить уравнение линейным уравнением $q=k·h$, где $k$ – некоторый коэффициент.
Предположим, что уровень воды изменяется в интервале от 0 до 1 м. Тогда один из вариантов – вычислить коэффициент как угол наклона отрезка, соединяющего точки кривой $q=α\sqrt{h}$. на концах этого интервала. Для определенности далее везде принимаем $α = 1$, тогда получаем $k = 1$.
Конечно, эта модель очень грубая и дает большую ошибку, особенно для уровней в диапазоне от 0.1 до 0.6. Чтобы уменьшить ошибку, можно попробовать несколько изменить $k$ (например, увеличив его до 1.2), однако точность приближения по-прежнему будет невысока, хотя и чуть-чуть лучше, чем в первом случае.
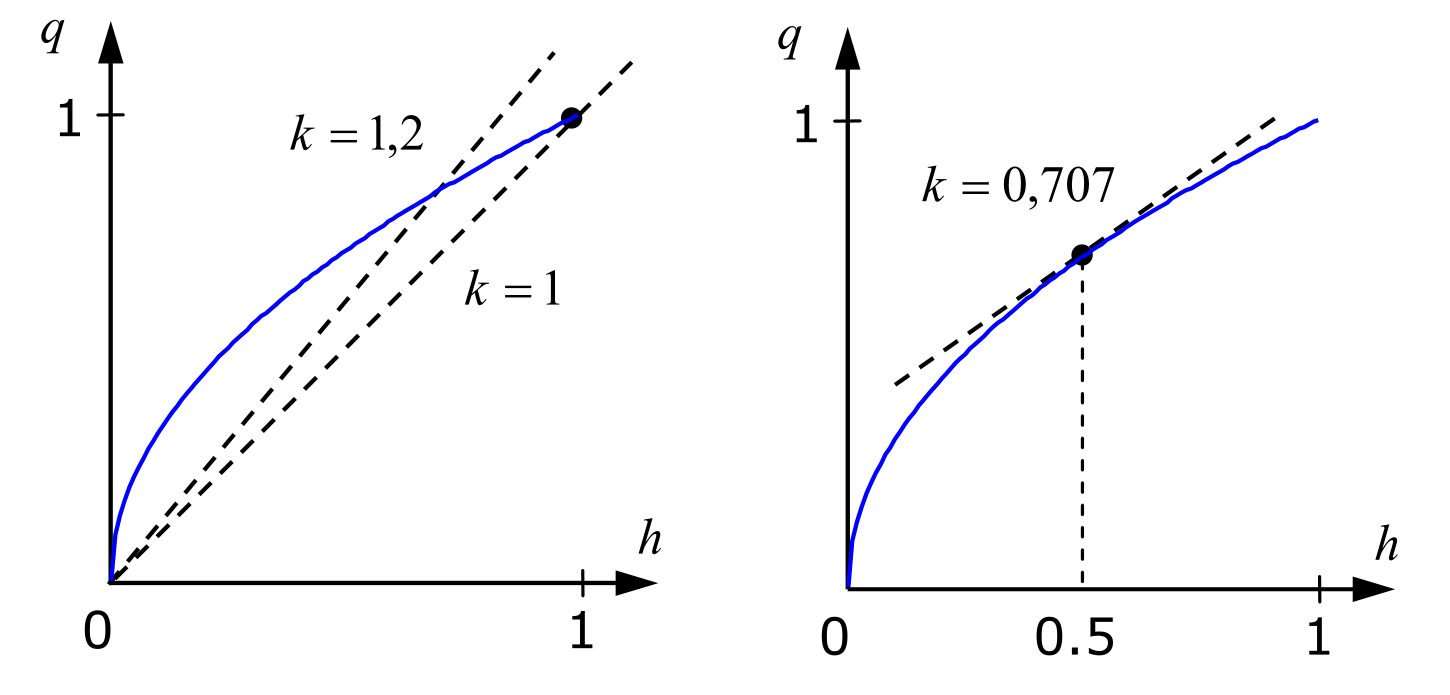
Теперь предположим, что обычно уровень мало изменяется вблизи среднего значения $h = 0.5$ м. В этом случае можно применить другой подход. Заметим, что в этой области кривая $q=α\sqrt{h}$. почти совпадает с касательной в точке ) ($0.5$; $\sqrt{2}/2$), угол наклона которой равен производной
$$k = \frac{\mathrm{d}q}{\mathrm{d}h} = \frac{1}{2\sqrt{h}} = \frac{\sqrt{2}}{2} ≈ 0.707.$$Касательная – это прямая с наклоном k, проходящая через точку ($0.5$; $\sqrt{2}/2$), ее уравнение имеет вид $q=k·h+b$. Свободный член $b$ определим из равенства
$$\frac{\sqrt{2}}{2} = k·h + b = \frac{\sqrt{2}}{2}·0.5 + b,$$ $$b = \frac{\sqrt{2}}{4} ≈ 0.354.$$так что получаем модель
$$q=\frac{\sqrt{2}}{2}·h + \frac{\sqrt{2}}{4}.$$Это линейное уравнение, однако модель – нелинейная, поскольку для нее не выполняется, например, свойство умножения на константу. Принцип суперпозиции также не выполняется.
Для того, чтобы получить линейную модель, нужно записать уравнения в отклонениях от рабочей точки ($h_0$; $q_0$), в которой мы определяли наклон касательной. Тогда
$$q_0+∆q = \frac{\sqrt{2}}{2}·(h_0+∆h)+\frac{\sqrt{2}}{4}.$$Поскольку график зависимости проходит через точку ($h_0$; $q_0$), можно применить равенство $q_0 = \frac{\sqrt{2}}{2}·h_0+\frac{\sqrt{2}}{4}$. Тогда
$$∆q = \frac{\sqrt{2}}{2}·∆h.$$Полученное таким образом уравнение – это линейная модель объекта, записанная в отклонениях входа и выхода от номинальной (рабочей) точки ($h_0$; $q_0$). Приближенная модель точнее всего соответствует объекту вблизи этой точки, а при больших отклонениях от нее ошибка может значительно возрастать.
На этом простом примере мы познакомились с основными принципами линеаризации нелинейных алгебраических уравнений.
Реальные объекты не могут мгновенно изменять свое состояние, поэтому вместо статических моделей для их исследования используют динамические модели, которые описываются дифференциальными уравнениями, содержащими производные (скорости изменения сигналов). Такие модели могут быть получены из физических законов. Во многих случаях более или менее точные модели представляют собой нелинейные дифференциальные уравнения, поэтому для того, чтобы применить теорию линейных систем, требуется линеаризация. При этом применяется почти та же методика, что и для алгебраических уравнений.
Идея линеаризации заключается в том, что в системах регулирования (поддержания заданных значений величин) сигналы мало отклоняются от рабочей точки – некоторого положения равновесия, в котором все сигналы имеют «правильные» значения и их производные равны нулю. Поэтому для решения задач управления часто достаточно использовать линейную модель в отклонениях от этой рабочей точки.
Модель, только что построенная для бака с водой, не совсем правильная, потому что не учитывает, что уровень в баке изменяется – уменьшается по мере вытекания воды. Кроме того, предположим, что для поддержания уровня используется насос, который подкачивает воду в бак, его расход обозначим через $Q$. Для такого объекта входом является расход $Q$, а выходом – изменение уровня $h$.
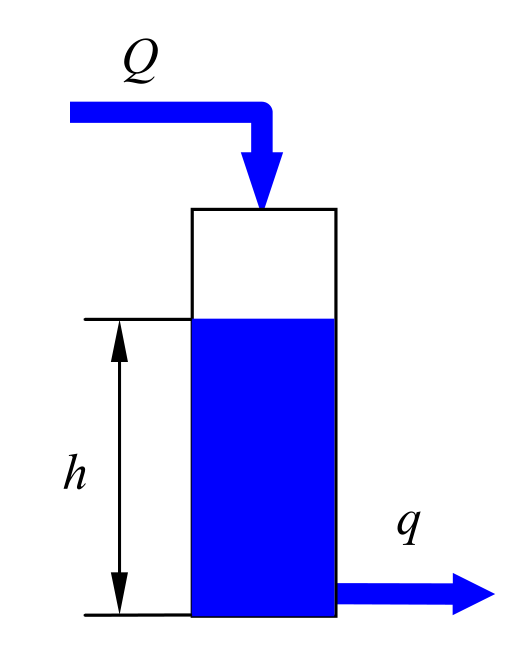
Предположим, что в течение маленького интервала $∆t$ расходы $Q$ и $q$ можно считать постоянным. За это время объем воды, добавленной в бак насосом, равен $Q·∆t$, а объем «ушедшей» воды – $q·∆t$. Учитывая, что площадь сечения бака равна $S$, получаем изменение уровня:
$$∆р=\frac{Q-q}{S}·∆t.$$Переходя к пределу при $∆t→0$, получаем дифференциальное уравнение
$$\frac{\mathrm{d}h(t)}{\mathrm{d}t} = \frac{1}{S}·[Q(t) - q(t)].$$Эта модель учитывает, что уровень воды и расходы изменяются во времени. Вспомним, что расход вытекающей жидкости $q(t)$ зависит от уровня воды в баке $h(t)$ и связан с ним нелинейной зависимостью $q(t)=α·\sqrt{h(t)}$. Поэтому уравнение можно записать в виде
$$\frac{\mathrm{d}h(t)}{\mathrm{d}t} = \frac{1}{S}·Q(t) - \frac{α}{S}·\sqrt{h(t)}.$$Здесь остались только две изменяющиеся величины: расход насоса $Q(t)$ (вход объекта) и уровень воды $h(t)$ (выход). Далее для упрощения записи мы не будем явно указывать зависимость этих сигналов от времени.
В установившемся (статическом) режиме, когда сигналы не изменяются, все производные равны нулю. В нашем случае, приняв $\frac{\mathrm{d}h(t)}{\mathrm{d}t} = 0$, получаем
$$0 = Q(t) - α\sqrt{h(t)}$$или
$$h(t)=\frac{Q(t)^2}{α^2} .$$Эта зависимость между установившимися значениями входа $Q$ и выхода $h$ называется статической характеристикой. Она позволяет для любого заданного постоянного значения $Q$ на входе получить значение выхода $h$.
Теперь предположим, что задана некоторая рабочая точка, то есть, значения входа $Q = Q_0$ и выхода $h = h_0$, и система все время работает около этого положения равновесия. Вблизи этой точки
$$Q(t) = Q_0 + ∆Q(t),$$ $$h(t) = h_0 + ∆h(t).$$где $∆Q(t)$ и $∆h(t)$ – малые отклонения входа и выхода от рабочей точки.
Дальше для линеаризации используется разложение функций в ряд Тейлора. Для некоторой функции $f(x,y)$ в окрестности точки $(x_0,y_0)$ этот ряд имеет вид:
$$f(x,y) = f(x_0,y_0 )+\frac{\partial f(x_0,y_0 )}{\partial x}·∆x + \frac{\partial f(x_0,y_0 )}{\partial y}·∆y + F(x,y),$$где $\frac{\partial f(x_0,y_0 )}{\partial x}$ и $\frac{\partial f(x_0,y_0 )}{\partial y}$ – частные производные функций $f(x,y)$ по $x$ и по $y$ в точке $(x_0,y_0)$, а $F(x,y)$ зависит от высших производных в той же точке (второй, третьей и т.д.). При малых значениях $∆x$ и $∆y$ можно считать, что «хвост» этого ряда $F(x,y)$ очень мал, примерно равен нулю, поэтому
$$f(x,y) ≈ f(x_0,y_0 )+\frac{\partial f(x_0,y_0 )}{\partial x}·∆x + \frac{\partial f(x_0,y_0 )}{\partial y}·∆y$$Применим эту формулу для линеаризации правой части нашего уравнения, где в роли $x$ выступает расход $Q$, а в роли $y$ – уровень $h$. Выполняя дифференцирование, находим
$$\frac{\partial }{\partial Q(t)}\ \left [\frac{1}{S}·Q(t) - \frac{α}{S}·\sqrt{h(t)}\right ] = \frac{1}{S},$$ $$\frac{\partial }{\partial h(t)}\ \left [\frac{1}{S}·Q(t) - \frac{α}{S}·\sqrt{h(t)}\right ] = \frac{-α}{2S\sqrt{h(t)}}.$$Тогда получаем
$$\frac{1}{S}·Q(t) - \frac{α}{S}·\sqrt{h(t)} ≈ \frac{1}{S}·Q_0 - \frac{α}{S}·\sqrt{h_0} + \frac{1}{S}·∆Q(t) - \frac{α}{2S\sqrt{h_0}}·∆h(t).$$Учитывая что
$$\frac{\mathrm{d}(h_0+∆h(t))}{\mathrm{d}t} = \frac{\mathrm{d}∆h(t)}{\mathrm{d}t}$$получим
$$\frac{\mathrm{d}∆h(t)}{\mathrm{d}t} ≈ \frac{1}{S}·Q_0 - \frac{α}{S}S\sqrt{h_0} + \frac{1}{S}·∆Q(t) - \frac{α}{2S\sqrt{h_0}}·∆h(t).$$Вспоминая, что $Q_0$ и $h_0$ соответствуют статическому режиму, то есть
$$\frac{1}{S}·Q_0 - \frac{α}{S}·\sqrt{h_0} = 0,$$получаем линеаризованное уравнение в отклонениях от рабочей точки:
$$\frac{\mathrm{d}∆h(t)}{\mathrm{d}t} + k_h·∆h(t) ≈ k_Q·∆Q(t),$$где $k_h=\frac{α}{2S\sqrt{h_0}}$ и $k_Q=\frac{1}{S}$. Заметим, что коэффициент $k_h$ зависит от $h_0$, то есть от выбора рабочей точки. В этом проявляется нелинейность объекта.
Но нужно помнить, что это уравнение в отклонениях, и оно справедливо только при малых отклонениях от рабочей точки ($Q_0$, $h_0$). При выборе другой рабочей точки коэффициент $k_h$ получится другой.
Посмотрим на примере, как можно управлять объектом и что из этого получается. Немного изменим предыдущую задачу, разрешив потоку вытекающей жидкости $q$ изменяться независимо (в теории управления это называется нагрузкой на объект).
Для того, чтобы обеспечить водой всех жителей деревни, построили водонапорную башню, в которую насосом закачивается вода из реки. Каждый житель может в любой момент включить воду на своем участке, например, для полива. Нужно построить систему, которая автоматически поддерживает заданный уровень $h_0$ воды в цистерне (в метрах).
Будем считать, что жителей довольно много, поэтому у кого-то всегда включена вода и насос постоянно работает на закачку воды в цистерну. Для управления уровнем воды $h$ мы можем изменять его поток $Q$ (м3/с). Таким образом, уровень $h$ – это регулируемая величина, а поток $Q$ – сигнал управления. Для обратной связи используем датчик, измеряющий уровень воды $h$ в цистерне.
Построим математическую модель объекта, то есть цистерны. Поток на выходе $q$ (м3/с) показывает, сколько воды вытекает из цистерны за 1 с – это нагрузка.
Изменение уровня $∆h$ зависит от разности потоков $Q - q$ и площади сечения цистерны $S$.
Если разность потоков постоянна в течение интервала времени $∆t$, то
$$∆h(t) = \frac{Q(t)-q(t)}{S}·∆t.$$В общем случае нужно использовать интеграл:
$$∆h(t)=\frac{1}{S}·∫_0^tQ(t)-q(t)\mathrm{d}t.$$Пусть в момент времени $t = 0$ уровень воды равен заданному значению, а входной и выходной потоки равны ($Q_0 = q_0$), так что уровень не меняется. Этот режим мы примем за номинальный (рабочую точку). Для того, чтобы получить уравнение в отклонениях, представим потоки в виде
$$Q(t) = Q_0+∆Q(t),$$ $$q(t) = q_0+∆q(t),$$где $∆Q(t)$ и $∆q(t)$ – малые отклонения потоков от номинального режима. Тогда можно записать модель объекта управления в форме
$$∆h(t) = \frac{1}{S}·∫_0^t∆Q(t)-∆q(t)\mathrm{d}t.$$Заметим, что эта модель может быть записана как дифференциальное уравнение (если найти производные обеих частей равенства):
$$\frac{\mathrm{d}∆h(t)}{\mathrm{d}t} = \frac{1}{S}·(∆Q(t)-∆q(t)).$$Для упрощения далее примем $S = 1$ м2.
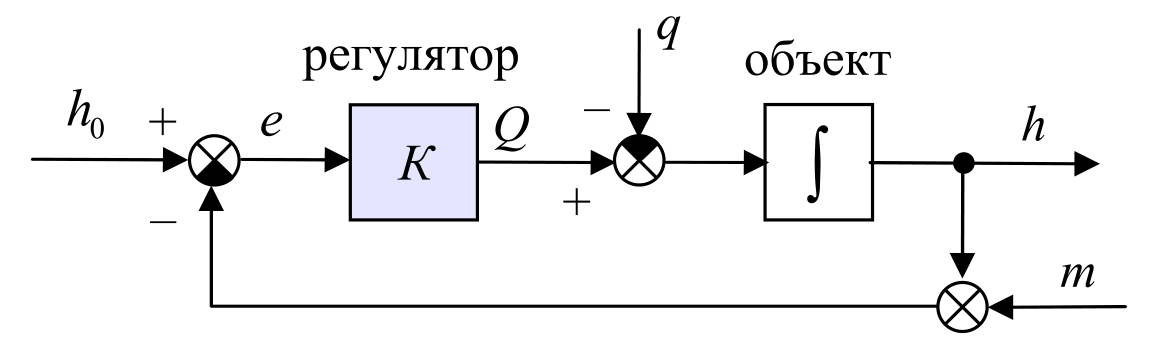
В качестве обратной связи мы будем использовать сигнал с датчика уровня. Ошибка управления вычисляется как разница между заданным и измеренным уровнями воды:
$$e(t) = h_0 - h(t).$$Применим самый простой регулятор – усилитель с коэффициентом $K$ (или пропорциональный регулятор, П-регулятор), который управляет потоком по закону
$$Q(t) = K·e(t) = K·(h_0-h(t)).$$Структурная схема системы управления показана на рисунке ниже. Знак интеграла обозначает звено, модель которого – оператор интегрирования. С помощью кружка с секторами обозначается сложение сигналов. Если какой-то сектор закрашен черным цветом, входящий в него сигнал вычитается (учитывается в сумме со знаком «минус»). Кроме сигналов, о которых уже шла речь, на рисунке показан также шум измерения $m(t)$, искажающий показания датчика.
Проверим работу этого регулятора при различных значениях коэффициента $K$. Сначала будем считать, что шума измерений нет, то есть уровень измеряется точно. Предположим, что расход воды на выходе $q$ увеличивается скачком (все начали поливать огороды). Синяя линия на рисунке показывает изменение уровня при $K = 1$, а зеленая – при $K = 5$.
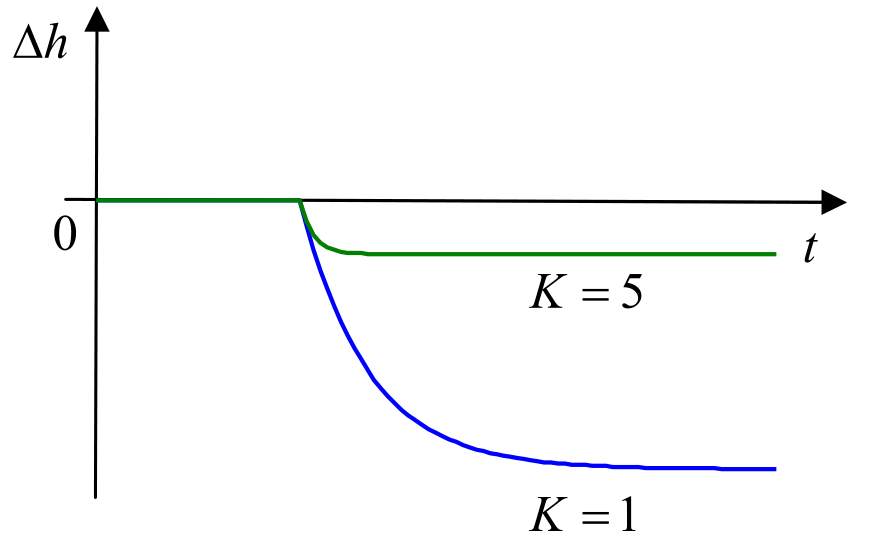
По этим данным можно сделать некоторые выводы:
Кажется, что для улучшения управления нужно увеличивать $K$, однако это только первое впечатление.
Теперь посмотрим, что будет, если есть шум измерений (случайная ошибка датчика).
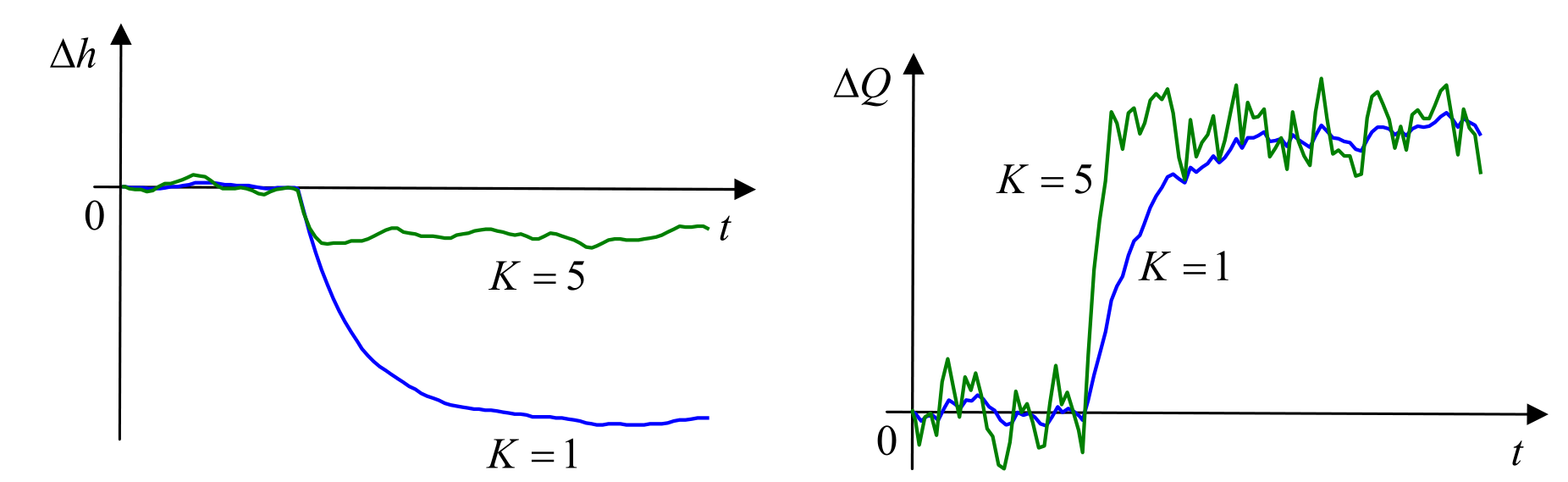
По графикам видно, что при неточных измерениях уровень колеблется около некоторого среднего значения (того, что было получено без шума), причем при бульшем $K$ колебания увеличиваются. Этот эффект особенно хорошо виден на графике изменения расхода насоса $∆Q$ (рисунок справа).
При увеличении $K$ повышение точности (уменьшение установившейся ошибки) достигается за счет повышенной активности насоса, который все время «дергается». При этом механические части изнашиваются, и существенно уменьшается его срок службы. Поэтому коэффициент $K$ нельзя сильно увеличивать.
Один из главных выводов этого примера: управление чаще всего связано с компромиссом. Здесь, с одной стороны, нужно увеличивать $K$, чтобы повысить точность, а с другой – нужно уменьшать $K$, чтобы уменьшить влияние шума измерения.