Систему управления можно разбить на блоки, имеющие вход и выход (объект, регулятор, привод, измерительная система). Для того, чтобы показать взаимосвязи этих блоков, используют структурные схемы. На них каждый элемент изображается в виде прямоугольника, внутри которого записывается его передаточная функция. Вход и выход блока показывают соответственно «входящей» и «выходящей» стрелками.

Строго говоря, есть две формы записи:
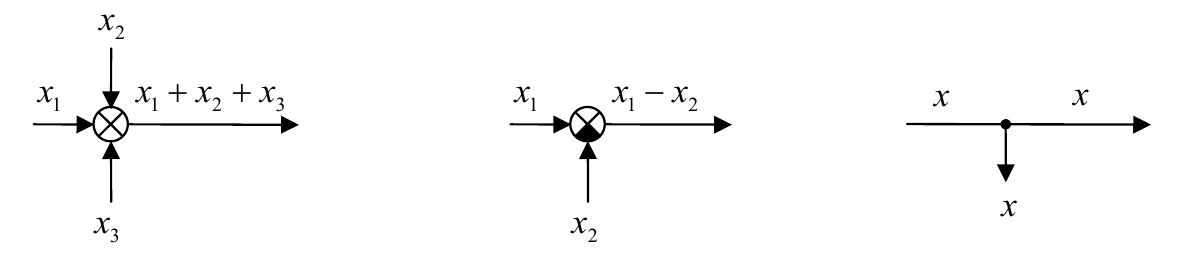
Для суммирующих элементов используют специальное обозначение – круг, разбитый на сектора. Если сектор залит черным цветом, поступающий в него сигнал вычитается, а не складывается с другими. Разветвление сигнала обозначается точкой, как и радиотехнике.
На следующем рисунке показана типичная схема системы управления кораблем по курсу. Здесь вход $x$ – заданный курс, выход $y$ – фактический курс. Сигналы $e$, $u$ и $δ$ обозначают соответственно ошибку регулирования, сигнал управления и управляющее воздействие привода на объект (угол поворота руля). Сигнал $g$ – это возмущение (влияние ветра и морского волнения), а $m$ – шум измерений.
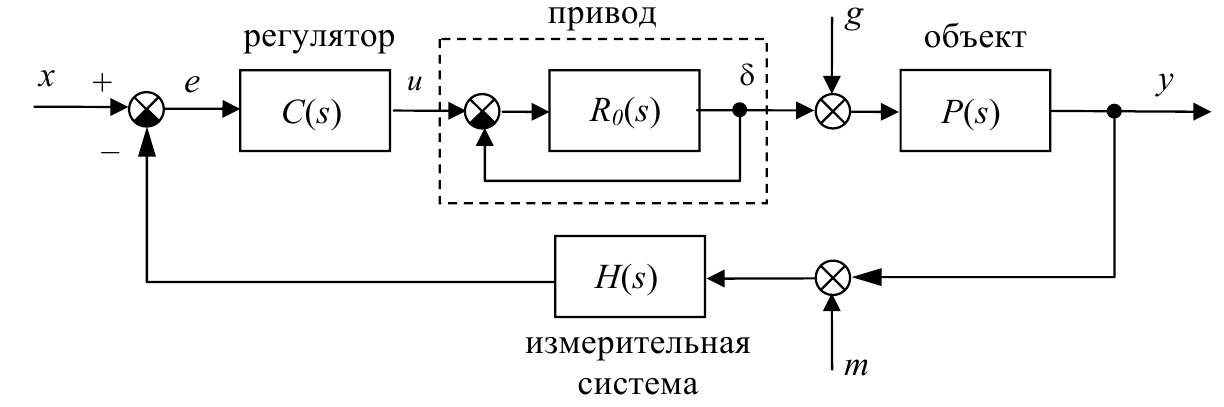
В этой системе кроме «большого» контура управления (регулятор – привод – объект) есть еще внутренний контур привода (звено с передаточной функцией $R_0 (s)$ охвачено отрицательной обратной связью).
Многие инженерные (классические) методы исследования систем управления основаны на использовании передаточных функций. Для построения передаточной функции системы между заданными входом и выходом нужно преобразовать структурную схему так, чтобы в конечном счете остался один блок с известной передаточной функцией. Для этого используют структурные преобразования.
Легко показать, что передаточные функции параллельного и последовательного соединений равны соответственно сумме и произведению исходных передаточных функций
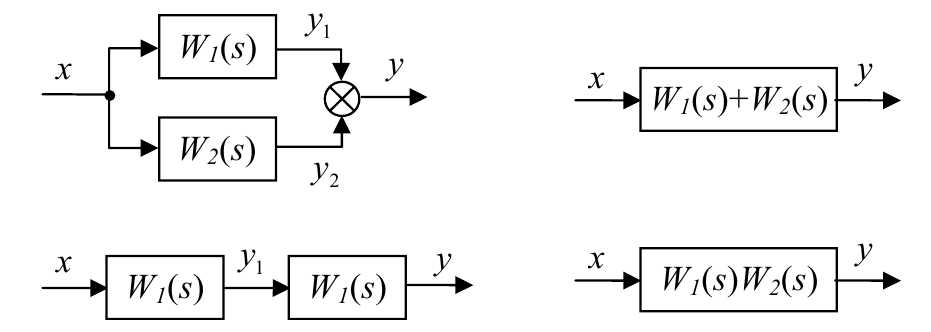
Действительно, в изображениях по Лапласу для параллельного соединения получаем
$$Y(s)=Y_1 (s)+Y_2 (s)=W_1 (s)·X(s)+W_2 (s)·X(s)=(W_1 (s)+W_2 (s))·X(s),$$а для последовательного
$$Y(s)=W_1 (s)·W_2 (s)·X(s).$$Для контура с отрицательной обратной связью имеем
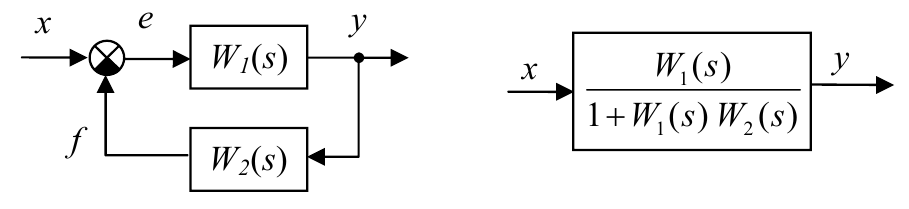
Для доказательства заметим, что $Y(s)=W_1 (s)·E(s)$, а изображение ошибки равно
$$E(s)=X(s)-F(s)=X(s)-W_2 (s)·Y(s).$$Поэтому
$$Y(s)=W_1 (s)·(X(s)-W_2 (s)·Y(s)).$$Перенося $Y(s)$ в левую часть, получаем
$$Y(s)=\frac{W_1 (s)}{1+W_1 (s)·W_2 (s) }·X(s).$$Если обратная связь – положительная (сигналы $x$ и $f$ складываются), в знаменателе будет стоять знак «минус»:
$$Y(s)=\frac{W_1 (s)}{1-W_1 (s)·W_2 (s) }·X(s).$$Звено можно переносить через сумматор как вперед, так и назад. Чтобы при этом передаточные функции не изменились, перед сумматором нужно поставить дополнительное звено:
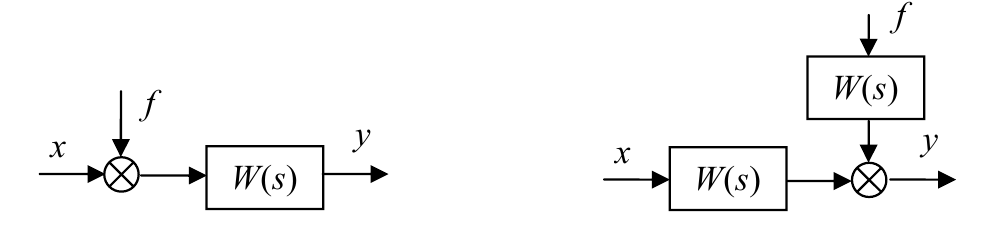
Обратите внимание, что передаточные функции от обоих входов к выходу на двух схемах одинаковые. Для следующей пары это условие тоже выполняется:
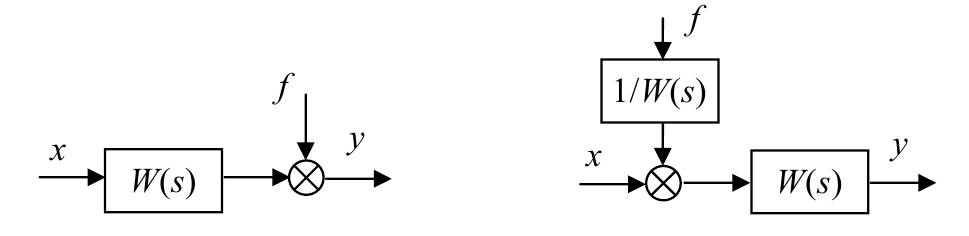
Звено можно переносить также через точку разветвления, сохраняя все передаточные функции:
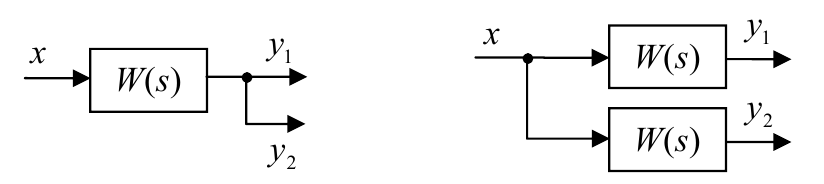
Эти две схемы тоже равносильны:
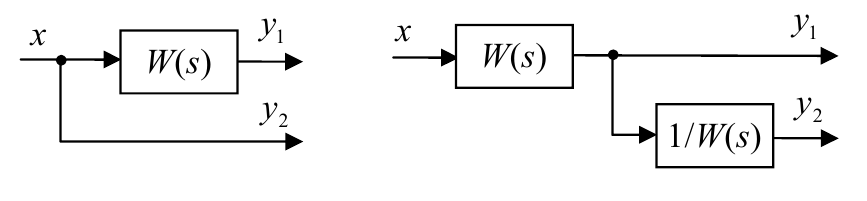
Применим показанные выше приемы для вычисления передаточных функций рассмотренной выше системы. Здесь три входа ($x$, $g$ и $m$), а в качестве выходов обычно рассматривают выход системы $y$, сигнал управления $u$ и ошибку $e$. Таким образом, всего можно записать 9 передаточных функций, соединяющих все возможные пары вход-выход.
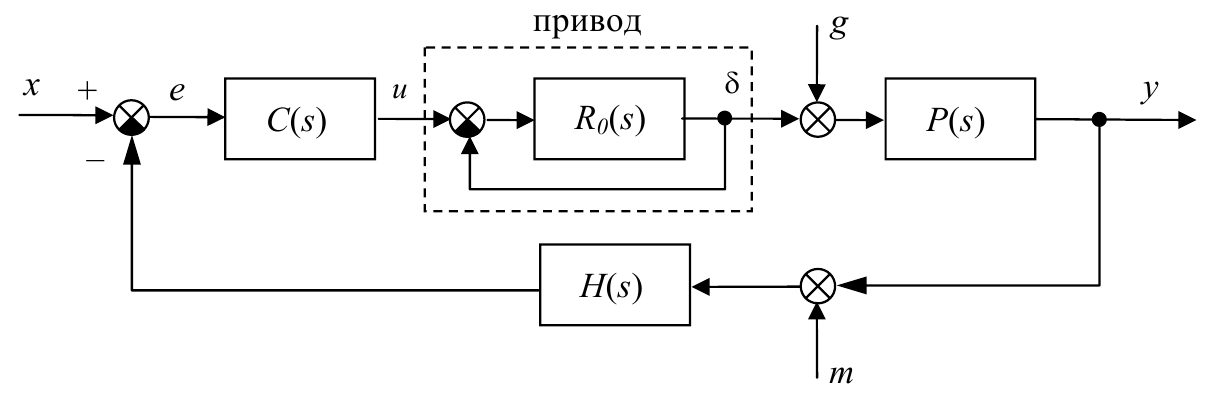
Сначала найдем полную передаточную функцию привода (обведенного штриховой рамкой), используя формулу для контура с отрицательной обратной связью:
$$R(s)=\frac{R_0 (s)}{1+R_0 (s) }.$$Получаем следующую схему:
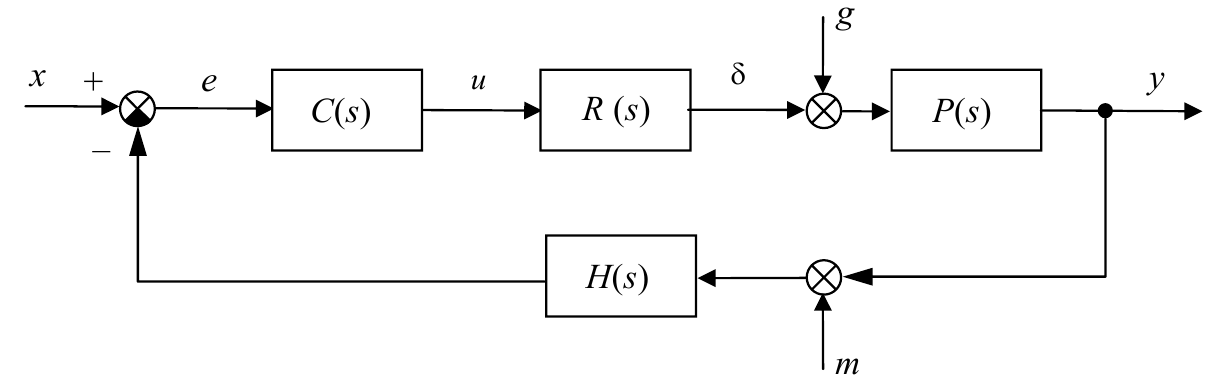
Теперь найдем передаточные функции от входа $x$ ко всем выходам. Для этого все остальные входы будем считать нулевыми и удалим со схемы. Кроме того, заменим последовательное соединение звеньев с передаточными функциями $C(s)$, $R(s)$ и $P(s)$ на одно звено:
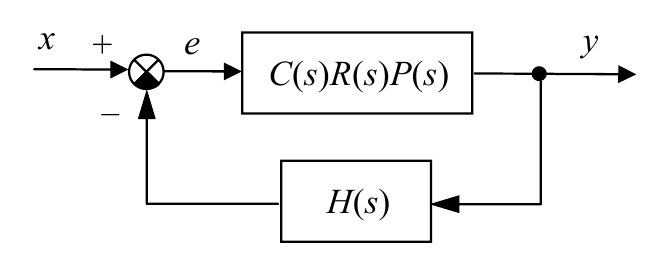
Для получения окончательного результата снова используем формулу для контура с отрицательной обратной связью:
$$W(s)=\frac{C(s)·R(s)·P(s)}{1+C(s)·R(s)·P(s)·H(s) }.$$