Что мы хотим от управления? Это зависит, прежде всего, от решаемой задачи. В задаче стабилизации наиболее важны свойства установившегося режима. Для следящих систем в первую очередь нужно обеспечить высокое качество переходных процессов при изменении задающего сигнала (уставки).
В целом можно выделить четыре основных требования:
Начнем с простого – покажем, как вычислить процесс на выходе системы с передаточной функцией $W(s)$ при входном сигнале, для которого известно изображение по Лапласу $X(s)$.
При нулевых начальных условиях изображение выхода равно
$$Y(s)=W(s)·X(s).$$Предположим, что $W(s)$ и $X(s)$ – рациональные функции, то есть их можно представить в виде отношения полиномов
$$W(s)=\frac{n_W (s)}{∆(s)} ,$$ $$X(s)=\frac{n_X (s)}{d_X (s)}.$$Для простоты будем считать, что полиномы $∆(s)$ и $d_X (s)$ имеют только простые вещественные корни, так что
$$∆(s)=(s-α_1 )(s-α_2 )…(s-α_N ),$$ $$d_X (s)=(s-β_1 )(s-β_2 )…(s-β_M ),$$причем общих корней у них нет. Числа $α_i$ ($i=1,…,N$) и $β_j$ ($j=1,…,M$) называются полюсами функций $W(s)$ и $X(s)$ соответственно.
При этих условиях произведение $Y(s)=W(s)·X(s)$ можно разложить на простые дроби
$$Y(s)=\frac{a_1}{s-α_1}+\frac{a_2}{s-α_2}+⋯+\frac{a_N}{s-α_N}+\frac{b_1}{s-β_1}+⋯+\frac{b_1}{s-β_1},$$Здесь $a_i$ ($i=1,…,N$) и $b_j$ ($j=1,…,M$) – постоянные, которые в данном случае определяются по формулам:
$$a_i=W(s)·X(s)·(s-α_1 )|_{s=α_i},$$ $$b_j=W(s)·X(s)·(s-β_1 )|_{s=β_i}.$$Далее мы предположим, что произведение $W(s)·X(s)$ несократимо. В этом случае все числа $a_i$ и $b_j$ не равны нулю.
Чтобы найти выход $y(t)$, нужно вычислить обратное преобразование Лапласа для $Y(s)$
$$y(t)=a_1 e^{α_1 t}+a_2 e^{α_2 t}+⋯a_N e^{α_N t}+b_1 e^{β_1 t}+⋯+a_M e^{α_M t}.$$Вспомним, что функция $e^{λt}$ при $t→∞$ стремится к нулю, если $λ < 0$; остается постоянной (равной $1$) при $λ=0$ и уходит в бесконечность при $λ > 0$. Поэтому данное выражение позволяет сделать следующие выводы:
Еще раз отметим, что мы предполагали несократимость произведения $W(s)·X(s)$, иначе некоторые коэффициенты $a_i$ и/или $b_i$ могут оказаться нулевыми и соответствующие экспоненты «исчезают» из формулы. Тогда, например, может оказаться, что выход не «уходит в бесконечность» даже если $W(s)$ или $X(s)$ имеет полюс с положительной вещественной частью.
Часть показателей экспонент (числа $α_i$ ($i=1,…,N$) полностью определяются свойствами системы – это корни полинома $∆(s)$. Если среди них есть числа с положительной вещественной частью, сигнал выхода будет неограниченно возрастать при любом входе, для которого произведение $W(s)·X(s)$ несократимо. В этом случае говорят, что система неустойчива, а соответствующие полюса также называют неустойчивыми. Полином $∆(s)$ называется характеристическим полиномом, так как расположение его корней определяет устойчивость (или неустойчивость) системы.
Точность системы обычно оценивается для одного из эталонных входных сигналов. Это может быть, например, единичный скачок
$$x(t)=1(t)=\begin{cases}0,t< 0\\1, t ≥ 0\end{cases},$$ $$X(s)=\frac{1}{s}$$или линейно возрастающий сигнал
$$x(t)=\begin{cases}0,t< 0\\t, t ≥ 0\end{cases},$$ $$X(s)=\frac{1}{s^2}$$или гармонический сигнал с частотой $ω$:
$$x(t)=sin(ω·t),$$ $$X(s)=\frac{ω}{s^2+ω^2}.$$Точность системы в установившемся режиме определяется ошибкой $e(t)$ или ее изображением $E(s)$. Для ее исследования используют передаточную функцию по ошибке $W_e (s)$, которая связывает изображения ошибки и входного сигнала:
$$E(s)=W_e (s)·X(s).$$Рассмотрим контур управления, состоящий из регулятора и объекта:
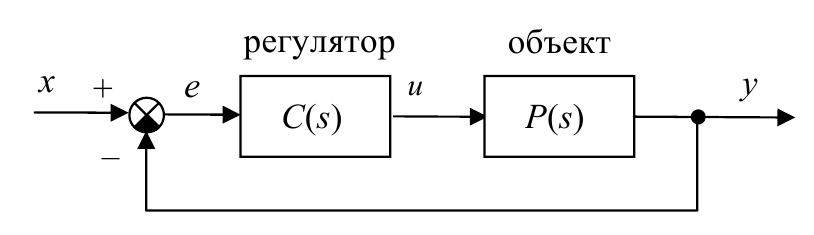
Представим передаточные функции $C(s)$ и $P(s)$, а также изображение входа $X(s)$ в виде отношения полиномов
$$C(s)=\frac{n_C (s)}{d_C (s)},$$ $$P(s)=\frac{n(s)}{d(s)},$$ $$X(s)=\frac{n_X (s)}{d_X (s)}.$$В данном случае передаточная функция по ошибке равна
$$W_e (s)=\frac{1}{1+C(s)·P(s)}=\frac{d_C (s)·d(s)}{∆(s)},$$где $∆(s)=d_C (s)·d(s)+n_C (s)·n(s)$ – характеристический полином замкнутой системы.
Рассмотрим реакцию системы на единичный ступенчатый входной сигнал, изображение которого равно $X(s)=1/s$. Сигнал ошибки определяется полюсами передаточной функции $W_e (s)$ (то есть корнями характеристического полинома $∆(s)$) и полюсами изображения $X(s)$. На практике все полюса $W_e (s)$ должны иметь отрицательные вещественные части, иначе система будет неустойчивой. Поэтому нулевых полюсов у функции $W_e (s)$ быть не может. Тогда
$$W_e (s)·X(s)=\frac{1}{1+C(s)·P(s)}·\frac{1}{s}=Y_0 (s)+\frac{b}{s}.$$Здесь изображение $Y_0 (s)$ имеет полюса только с отрицательной вещественной частью, а постоянная $b$ рассчитывается по формуле разложения на простые дроби:
$$b=\frac{1}{1+C(0)·P(0)}=\frac{d_C (0)·d(0)}{∆(0)}.$$После затухания всех экспонент с отрицательными показателями получим
$$\lim_{t\to ∞} e(t)=b.$$Заметим, что для того, чтобы сделать нулевой статическую ошибку, достаточно обеспечить $d_C (0)=0$, то есть регулятор должен содержать интегратор) или $d(0)=0$ (объект содержит интегратор).
Этот результат можно обобщить для любых незатухающих входных сигналов, изображения которых имеют полюса на мнимой оси (в точке $s=0$ или в точках $s=±jω$). Для того, чтобы ошибка стремилась к нулю при $t→∞$ необходимо, чтобы эти полюса сократились в произведении
$$W_e (s)·X(s)=\frac{d_C (s)·d(s)}{∆(s)}·\frac{n_X (s)}{d_X (s)}.$$А это, в свою очередь, возможно только тогда, когда они являются корнями полинома $d_C (s)·d(s)$, то есть, внутри системы есть модель входного сигнала. Этот принцип называется принципом внутренней модели.
Например, для точного отслеживания ступенчатого сигнала нужно, чтобы объект или регулятор содержали интегрирующее звено (с передаточной функцией $\frac{1}{s}$). Тогда произведение $d_C (s)·d(s)$ имеет сомножитель $s$, и полюс $X(s)$ в точке $s=0$ сократится в произведении $W_e (s)·X(s)$. Таким образом, если передаточная функция разомкнутого контура $C(s)·P(s)$ содержит множитель $s$ в знаменателе, обеспечивается нулевая ошибка слежения за постоянным сигналом (нулевая статическая ошибка). Поэтому такую систему называют астатической.
Для отслеживания линейно возрастающего сигнала в контуре должно быть уже два интегратора (нужно сократить двойной полюс $X(s)$ в точке $s=0$). Такая система обладает астатизмом второго порядка. В общем случае система, в которой
$$C(s)·P(s)=\frac{1}{s^v}·G(s),$$где $ν>0$ – натуральное число и функция $G(s)$ не имеет нулей и полюсов в точке $s=0$, называется астатической системой ν-ого порядка. Такая система в установившемся режиме без ошибки отслеживает сигнал вида
$$x(t)=x_0+x_1 t+x_2 t^2+⋯+x_(v-1) t^(v-1)$$при любых значениях коэффициентов $x_i$ ($i=0,…,v-1$).
Казалось бы, для повышения точности можно поставить много интеграторов, и все проблемы будут решены. Но при этом нужно учесть, что мы говорили только о точности в установившемся режиме, не затрагивая переходные процессы (переход с режима на режим) и вопросы устойчивости. Добавление каждого нового интегратора ухудшает переходные процессы, осложняет стабилизацию системы, снижает быстродействие. Например, двойным интегратором в принципе невозможно управлять с помощью простого регулятора-усилителя (так называемого пропорционального регулятора или П-регулятора). Кроме того, если разомкнутая система включает два интегратора и более, для сигнала ошибки $e(t)$ справедливо ограничение
$$∫_0^∞ e(t)\mathrm{d}t=0.$$Поскольку интеграл от ошибки равен нулю, часть времени ошибка должна быть положительной, а часть – отрицательной. Поэтому при любом управлении не удастся получить монотонный переходный процесс (когда сигнал выхода подходит к заданному значению «с одной стороны», как у апериодического звена).
Для стохастической системы, в которой все процессы имеют случайный характер, точность оценивается с помощью математического ожидания и дисперсии ошибки.
Понятие устойчивости известно нам с детства. Например, табуретка с двумя ножками неустойчива, она упадет при малейшем дуновении ветра, а с тремя – устойчива. Всем знакомый пример неустойчивой системы – близко расположенные микрофон и колонки, которые начинают «свистеть».
Термин «устойчивость» используется в численных методах, механике, экономике, социологии, психологии. Во всех этих науках имеют в виду, что устойчивая система возвращается в состояние равновесия, если какая-то сила выведет ее из этого состояния. Шарик на рисунке находится в устойчивом равновесии в положении А – если немного сдвинуть его с места, он скатится обратно в ямку.
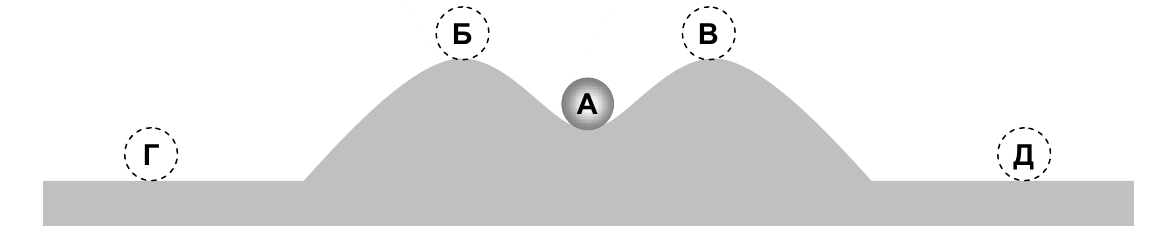
Однако мы можем заметить, что если шарик сильно отклонить от равновесия, он может свалиться через горку вбок, то есть устойчивость нарушится.
В положениях Б и В шарик также находится в положении равновесия, но оно неустойчиво, так как при малейшем сдвиге в сторону шарик скатывается с вершины.
В положениях Г и Д равновесие шарика нейтральное – при небольшом смещении он остается в новом положении. При этом говорят, что система нейтрально устойчива, то есть находится на границе устойчивости.
Можно показать, что система «шарик-горка» – нелинейная. Как мы увидели, для нее
Известно несколько определений устойчивости, которые отличаются некоторыми деталями. Если рассматривается только выход системы при различных ограниченных входах, говорят об устойчивости «выход-выход».
Кроме того, часто изучают устойчивость автономной системы, на которую не действуют внешние сигналы (все входы нулевые). Предполагается, что систему вывели из положения равновесия (задали ненулевые начальные условия) и «отпустили». Система, которая сама возвращается в исходное положение равновесия, называется устойчивой. Если при этом рассматривается только выход системы (а не ее внутренние сигналы), говорят о «технической устойчивости» (или устойчивости по выходу). Напротив, внутренняя или математическая устойчивость означает, что не только выход, но и все внутренние переменные (переменные состояния) приближаются к своим значениям в положении равновесия.
В некоторых задачах основной рабочий режим – это периодические колебания, поэтому можно рассматривать устойчивость процессов, а не только положения равновесия.
Устойчивость «вход-выход». Обычно для инженеров практиков в первую очередь важно, чтобы система не «пошла вразнос», то есть, чтобы управляемая величина не росла неограниченно при всех допустимых входных сигналах. Если это так, говорят, что система обладает устойчивостью «вход-выход» (при ограниченном входе выход также ограничен). Заметим, что при этом нас не интересует, как меняются внутренние переменные объекта, важен только вход и выход.
«Техническая» устойчивость. В отличие от устойчивости «вход-выход», понятие «техническая устойчивость» относится к автономной системе, у которой все входные сигналы равны нулю.
Положением равновесия называют состояние системы, которая находится в покое, то есть, сигнал выхода $y(t)$ – постоянная величина, и все его производные равны нулю.
Систему выводят из положения равновесия и убирают все возмущения. Если при этом с течением времени (при $t→∞$) система возвращается в положение равновесия, она называется устойчивой. Если выходная координата остается ограниченной (не уходит в бесконечность), система называется нейтрально устойчивой, а если выход становится бесконечным – неустойчивой.
Внутренняя устойчивость. Говоря о внутренней устойчивости, рассматривают не только выход, но и все переменные, описывающие состояние системы. В математической теории систем вектор состояния обозначают через $x(t)$, а уравнение движения системы записывают в виде
$$\frac{\mathrm{d}x(t)}{\mathrm{d}t}=f(x,t).$$Фактически это система дифференциальных уравнений первого порядка, в нем правая часть зависит только от значений $t$ и $x(t)$, но не от производных. Если вектор состояния $x(t)$ состоит из двух компонентов, $x_1 (t)$ и $x_2 (t)$, уравнение можно записать в развернутой форме
\begin{cases}\frac{\mathrm{d}x_1 (t)}{\mathrm{d}t}=f_1 (x,t)\\ \frac{\mathrm{d}x_2 (t)}{\mathrm{d}t}=f_2 (x,t)\end{cases}где функции $f_1 (x,t)$ и $f_2 (x,t)$ зависят от вектора состояния и времени.
Устойчивость определяется для некоторого положения равновесия. Для нелинейной системы может быть несколько положений равновесия, причем некоторые из них могут быть устойчивы, а некоторые – нет. В положении равновесия все производные равны нулю, то есть $f(x^*,t)=0$, где $x^*$ – соответствующий вектор состояния.
Предположим, что систему вывели в некоторое начальное состояние $x_0=x(0)$ (задали начальные условия), а потом внешнее воздействие прекратили. Дальнейшее изменение координат («движение» системы $x(t)$) можно найти как решение уравнения при заданных начальных условиях.
Нестрого говоря, устойчивость означает, что все движения $x(t)$, которые начинаются близко от положения равновесия $x^*$, при всех $t$ остаются в некоторой окрестности $x^*$.
Лучше, конечно, если система не просто устойчива, а еще и возвращается в положение равновесия, то есть, $x(t)$ стремится к $x^*$ при $t→∞$. В этом случае говорят об асимптотической устойчивости.
Рассмотрим маятник на рисунке а), состоящий из подвешенного металлического стержня и шарика. Здесь положение равновесия – шарик в нижней точке. Если не учитывать трение, маятник, выведенный из положения равновесия, будет качаться бесконечно долго, причем амплитуда колебаний не будет увеличиваться, то есть, система устойчива.

В реальности трение, конечно, есть, поэтому колебания маятника будут постепенно затухать (амплитуда уменьшается), и система в конце концов возвращается в положение равновесия. Это значит, что маятник с трением – асимптотически устойчивая система.
Маятник на рисунке б) тоже находится в положении равновесия, но оно неустойчиво: при малейшем отклонении маятник упадет вниз.
Формальное определение внутренней устойчивости было введено в работах А.М. Ляпунова, поэтому такое понятие устойчивости принято называть устойчивостью по Ляпунову.
Для простоты рассмотрим систему первого порядка, с одной переменной состояния $x(t)$.
Система называется устойчивой по Ляпунову в положении равновесия $x^*$, если при начальном отклонении от положения равновесия $x^*$ не более, чем на $δ$, траектория движения отклоняется от $x^*$ не более, чем на $ε$, причем для каждого $ε$ можно найти соответствующее ему $δ(ε)$:
$$|x_0-x^* | < δ,$$ $$|x(t)-x^* | < ε$$при всех $t > 0$.
Фактически это означает, что чем меньше начальное отклонение, тем меньше траектория движения отклоняется от положения равновесия.
Если кроме того вектор состояния стремится к положению равновесия, то есть $|x(t)-x^* |→0$ при $t→∞$, система называется асимптотически устойчивой в положении равновесия $x^*$. Заметим, что выполнение условия сходимости не гарантирует устойчивость по Ляпунову. Существуют примеры достаточно сложных нелинейных систем, в которых даже при очень малых отклонениях от положения равновесия сначала наблюдается большой «выброс», а затем траектория сходится к точке равновесия.
Очевидно, что асимптотическая устойчивость – более сильное требование. Положения равновесия, которые устойчивы по Ляпунову, но не асимптотически устойчивы, иногда называются нейтрально устойчивыми (маятник без трения).
Положение равновесия неустойчиво, если для него не выполняется условие устойчивости Ляпунова. Это значит, что существует такое $ε>0$, что траектория $x(t)$ выходит за границы области $|x(t)-x^*| < ε$ при сколь угодно малом отклонении начального состояния $x_0$ от положения равновесия $x^*$. Например, система переходит в другое положение равновесия, или $x(t)$ неограниченно возрастает.
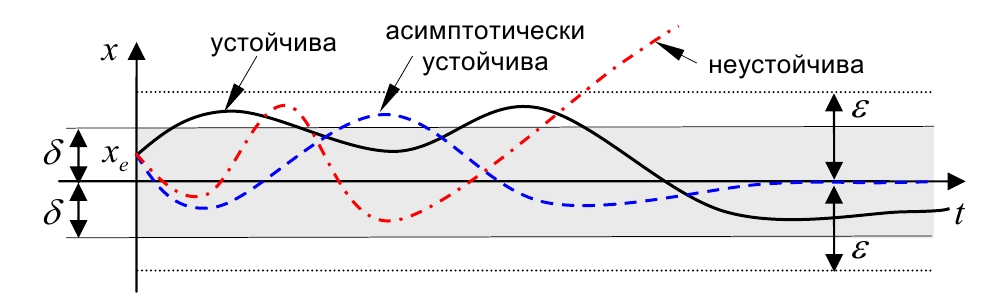
На следующем рисунке показаны движения устойчивой, асимптотически устойчивой и неустойчивой систем первого порядка (с одной координатой $x(t)$).
Если вектор состояния содержит несколько переменных, для оценки разности векторов $x_0-x^*$ и $x(t)-x^*$ вместо модуля используют евклидову норму (корень из суммы квадратов отклонений по каждой координате). Например, для системы второго порядка
$$‖x(t)-x_e‖=\sqrt{(x_1 (t)-x_1^*)^2+(x_2 (t)-x_2^*)^2},$$где $x_1^*$ и $x_2^*$ – компоненты вектора $x^*$.
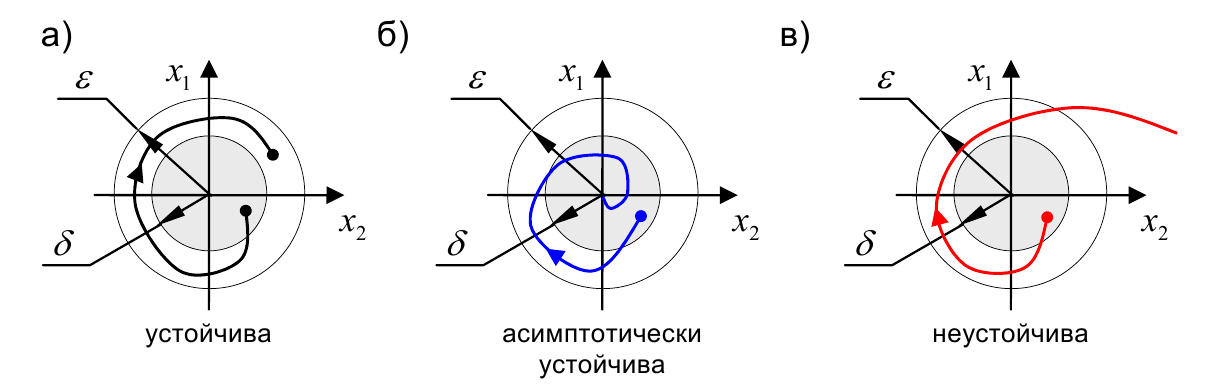
Траекторию движения систем второго порядка обычно изображают на фазовой плоскости, где по одной оси откладывается $x_1 (t)$, а по другой – $x_2 (t)$. На следующем рисунке показаны движения устойчивой, асимптотически устойчивой и неустойчивой систем. Для простоты предполагается, что положение равновесия – это начало координат, где $x_1=x_2=0$.
Линейные системы обладают рядом особенностей, которые во многих случаях упрощают анализ устойчивости:
Для того, чтобы получить условия устойчивости, рассмотрим уравнение движения линейной системы, на которую не действуют возмущения. Пусть $W(s)$ – ее передаточная функция.
Будем считать, что она имеет только простые (не кратные) полюса $α_i$ ($i=1,…,N$) (корни знаменателя):
$$W(s)=\frac{n_W (s)}{∆(s)} =\frac{n_W (s)}{(s-α_1 )(s-α_2 )…(s-α_N )},$$где $n_W (s)$ и $∆(s)$ – полиномы. Из теории линейных дифференциальных уравнений известно, что при отсутствии возмущений выход такой системы можно представить в виде:
$$y(t)=a_1 e^{α_1 t}+a_2 e^{α_2 t}+⋯+a_N e^{α_N t},$$где $a_i$ ($i=1,…,N$) – постоянные, которые определяются начальными условиями. Таким образом, процесс $y(t)$ затухает при любых начальных условиях тогда и только тогда, когда все корни $α_i$ ($i=1,…,N$) имеют отрицательные вещественные части. В этом случае система асимптотически устойчива.
Поскольку устойчивость линейной системы определяют корни полинома $∆(s)$ – знаменателя передаточной функции $W(s)$, этот полином называется характеристическим полиномом системы.
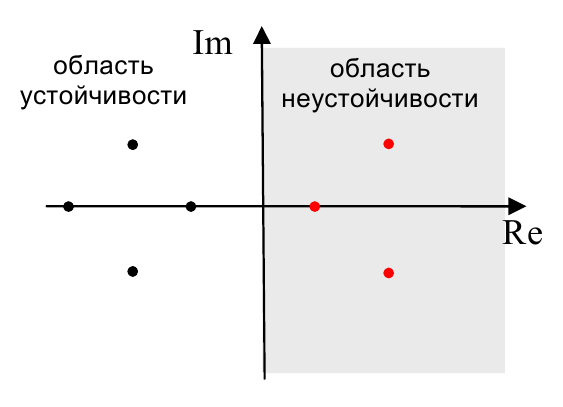
Если показать корни характеристического полинома (в общем случае – комплексные числа) на комплексной плоскости, то слева от мнимой оси будут устойчивые корни (с отрицательной вещественной частью), а справа – неустойчивые. Таким образом, область устойчивости – это левая полуплоскость.
Предположим, что один из корней полинома $∆(s)$ равен нулю (скажем, $α_1=0$), а остальные устойчивы, то есть, их вещественные части отрицательные. Это значит, что система содержит интегрирующее звено. Учитывая, что $e^{α_1 t}=e^0=1$ при всех $t$, получаем
$$y(t)=a_1+a_2 e^{α_2 t}+⋯+a_N e^{α_N t}.$$Здесь все слагаемые в правой части, кроме первого, затухают с течением времени, а постоянная составляющая $a_1$ остается. С другой стороны, выход не возрастает неограниченно, поэтому система нейтрально устойчива.
Теперь допустим, что характеристический полином имеет пару чисто мнимых корней: $α_1=jω$ и $α_2=-jω$. Это значит, что система содержит консервативные звено – генератор колебаний. При этом процесс на выходе системы содержит слагаемые $a_1 e^{jωt}$ и $a_2 e^{-jωt}$, которые могут быть (с помощью формулы Эйлера) представлены в виде
$$a_1 e^{jωt}=a_1 (cos(ωt)+j·sin(ωt)),$$ $$a_2 e^{-jωt}=a_2 (cos(ωt)-j·sin(ωt)).$$Эти составляющие дают незатухающие колебания (по крайней мере, для некоторых начальных условий), поэтому система находится на границе устойчивости (нейтрально устойчива). Заметим, что постоянные $a_1$ и $a_2$ – комплексно-сопряженные, то есть, если $a_1=b+jc$, то $a_2=b-jc$. При этом сумма
$$a_1 e^{jωt}+a_2 e^{-jωt}=2b·cos(ωt)-2c·sin(ωt)$$не содержит мнимой части.
Внутренняя устойчивость линейных систем. В предыдущем параграфе мы фактически рассмотрели техническую устойчивость, то есть, устойчивость по выходу при ненулевых начальных условиях.
Теперь посмотрим, как определить внутреннюю устойчивость линейной системы, то есть, устойчивость внутренних процессов. Поскольку выход системы нас пока не интересует, используем модель «вход-состояние»:
$$\frac{\mathrm{d}x(t)}{\mathrm{d}t}=A·x(t)+B·u(t),$$где $x(t)$ – вектор состояния, $u(t)$ – входной сигнал, A и B – постоянные матрицы. Если вход равен нулю (нет возмущений), уравнение упрощается
$$\frac{\mathrm{d}x(t)}{\mathrm{d}t}=A·x(t).$$Таким образом, свободное движение определяется только свойствами матрицы A.
Сначала для простоты будем считать, что матрица A имеет вид
$$A=\begin{bmatrix}α_1&0\\0&α_2\end{bmatrix}$$Тогда уравнение распадается на два независимых уравнения (две подсистемы):
$$\frac{\mathrm{d}x_1 (t)}{\mathrm{d}t}=α_1 x(t),$$ $$\frac{\mathrm{d}x_2 (t)}{\mathrm{d}t}=α_2 x(t).$$Здесь устойчивость определяется значениями $α_1$ и $α_2$. Если они оба отрицательны, то система асимптотически устойчива. Если одно из них – нуль, а второе отрицательно (или оба нулевых), то система нейтрально устойчива.
В общем случае внутренняя устойчивость зависит от собственных чисел матрицы $A$, то есть, от корней характеристического уравнения $det(λI-A)=0$, где $I$ – единичная матрица, а $det$ обозначает определитель квадратной матрицы. Полином $det(λI-A)$ от переменной $λ$ называют характеристическим полиномом. Например, для рассмотренной выше диагональной матрицы $A$
$$det(λI-A)=det\left(λ\begin{bmatrix}1&0\\0&1\end{bmatrix}-\begin{bmatrix}α_1&0\\0&α_2\end{bmatrix}\right)=(λ-α_1 )(λ-α_2 ).$$Очевидно, что корни этого полинома – это $α_1$ и $α_2$.
Если все корни характеристического полинома устойчивы (имеют отрицательные вещественные части, расположены в левой полуплоскости), то система асимптотически устойчива.
Если есть неустойчивые корни (с положительной вещественной частью), то система неустойчива. Если характеристический полином имеет один нулевой корень или пару комплексносопряженных корней на мнимой оси, система нейтрально устойчива.
Внутренняя устойчивость – более сильное требование, чем техническая устойчивость, потому что определяет ограниченность не только выхода, но и всех внутренних переменных при любых начальных условиях. Рассмотрим, например, такую модель в пространстве состояний
$$\frac{\mathrm{d}x(t)}{\mathrm{d}t}=\begin{bmatrix}1&0\\0&-1\end{bmatrix}x(t)+\begin{bmatrix}1\\0\end{bmatrix}u(t),$$ $$y(t)=\begin{bmatrix}0&1\end{bmatrix}x(t).$$Здесь матрица $A=\begin{bmatrix}1&0\\0&-1\end{bmatrix}$ имеет собственные числа $1$ и $–1$, причем первое из них – неустойчиво, поэтому система внутренне неустойчива.
Теперь найдем передаточную функцию:
$$W(s)=\begin{bmatrix}0&1\end{bmatrix}·\left(s\begin{bmatrix}1&0\\0&1\end{bmatrix}-\begin{bmatrix}1&0\\0&-1\end{bmatrix}\right)^{-1}·\begin{bmatrix}1\\0\end{bmatrix}=\frac{1}{s+1}.$$Ее знаменатель (характеристический полином) $∆(s)=s+1$ устойчив, так как имеет единственный устойчивый корень $−1$, хотя система внутренне неустойчива! Обратите внимание, что система имеет порядок 2, а знаменатель передаточной функции – порядок 1. В данном случае это означает, что некоторые внутренние движения системы не наблюдаемы на выходе, не влияют на него.
Вспомним, что передаточная функция описывает свойства системы только при нулевых начальных условиях. Поэтому выводы об устойчивости внутренних процессов в системе, сделанные по передаточной функции, могут оказаться неверными, если степень ее знаменателя меньше порядка исходного дифференциального уравнения.
Устойчивость линеаризованных систем. Устойчивость нелинейной системы можно во многих случаях оценивать с помощью линеаризованной системы. Для этого применяют теоремы Ляпунова, которые связывают корни характеристического полинома $∆(s)$ линейной модели и устойчивость нелинейной системы в окрестности точки линеаризации:
Таким образом, для исследования устойчивости положения равновесия нелинейной системы нужно линеаризовать модель в окрестности этой точки и найти корни характеристического полинома.
Итак, для исследования устойчивости линейной системы достаточно найти корни ее характеристического полинома. Если все корни имеют отрицательные вещественные части (находятся в левой полуплоскости, слева от мнимой оси), такой полином называется устойчивым, потому что соответствующая линейная система устойчива. Полиномы, имеющие хотя бы один корень с положительной вещественной частью (в правой полуплоскости) называются неустойчивыми.
На ранней стадии развития теории управления актуальной была задача определения устойчивости полинома без вычисления его корней. Конечно, сейчас легко найти корни характеристического полинома с помощью компьютерных программ, однако такой подход дает нам только количественные (а не качественные) результаты и не позволяет исследовать устойчивость теоретически, например, определять границы областей устойчивости.
Существует несколько алгоритмов, позволяющих проверить устойчивость полинома
$$∆(s)=a_0 s^n+a_1 s^{n-1}+⋯+a_{n-1} s+a_n,$$не вычисляя его корни. Прежде всего, для устойчивости все коэффициенты $a_i$ ($i=1,…,n$) должны быть одного знака, обычно считают, что они положительные. Это необходимое условие устойчивости полинома. Однако при $n>2$ это условие недостаточно, если полином имеет комплексно-сопряженные корни. Поэтому были разработаны необходимые и достаточные условия (критерии) устойчивости полиномов.
Один из самых известных критериев – критерий Гурвица – использует матрицу $H_n$ размером n×n, составленную из коэффициентов полинома $∆(s)$ следующим образом:
Критерий Гурвица. Все корни полинома $∆(s)$ имеют отрицательные вещественные части тогда и только тогда, когда все $n$ главных миноров матрицы $H_n$ (определителей Гурвица) положительны.
Вспомним, что для устойчивости полинома необходимо, чтобы все его коэффициенты были положительными. Поэтому достаточно проверить только $n-1$ первых определителей Гурвица. Например, для $n=5$ речь идет об определителях
$$D_1=a_1>0,$$ $$D_2=\begin{bmatrix}a_1&a_3\\a_0&a_2\end{bmatrix}>0,$$ $$D_3=\begin{bmatrix}a_1&a_3&a_5\\a_0&a_2&a_4\\0&a_1&a_3\end{bmatrix}>0,$$ $$D_4=\begin{bmatrix}a_1&a_3&a_5&0\\a_0&a_2&a_4&0\\0&a_1&a_3&a_5\\0&a_0&a_2&a_4\end{bmatrix}>0.$$Раскрывая определитель матрицы $H_5$ по последнему столбцу, получаем $D_5=det(H_5 )=a_5 D_5$. Так как $a_5>0$, из условия $D_4>0$ сразу следует $D_5>0$.
Таким образом, условия устойчивости сводятся к нескольким неравенствам. Это очень удобно для систем низкого порядка. Например, для $n=2$ необходимое и достаточное условие устойчивости – положительность всех коэффициентов полинома. Для $n=3$ характеристический полином имеет вид $∆(s)=a_0 s^3+a_1 s^2+a_2 s+a_3$, поэтому условия Гурвица определяются матрицей
$$H_3=\begin{bmatrix}a_1&a_3&0\\a_0&a_2&0\\0&a_1&a_3\end{bmatrix},$$ $$a_0>0.$$Полином устойчив, если все коэффициенты положительны и
$$D_2=\begin{bmatrix}a_1&a_3\\a_0&a_2\end{bmatrix}=a_1 a_2-a_0 a_3>0.$$Рассмотрим систему, в которой объект и регулятор задаются передаточными функциями:
$$P(s)=\frac{1}{(T_1 s+1)(T_2 s+1)} ,$$ $$C(s)=\frac{K}{s}.$$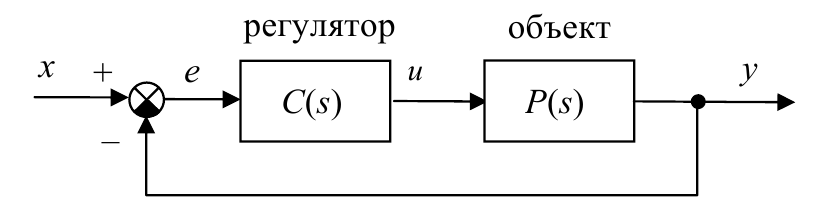
С помощью критерия Гурвица можно определить, при каких значениях $K$ замкнутая система (с отрицательной обратной связью) устойчива. Передаточная функция замкнутой системы равна
$$W(s)=\frac{C(s)P(s)}{1+C(s)P(s)}=\frac{K}{∆(s)},$$где характеристический полином имеет вид
$$∆(s)=(T_1 s+1)(T_2 s+1)s+K=T_1 T_2 s^3+(T_1+T_2 ) s^2+s+K.$$Необходимое условие устойчивости дает $K>0$. Применяя критерий Гурвица для системы третьего порядка, получаем
$$T_1+T_2>KT_1 T_2$$или
$$K < \frac{1}{T_1} + \frac{1}{T_2}.$$Таким образом, система устойчива при
$$0< K < \frac{1}{T_1} + \frac{1}{T_2} .$$Критерий Найквиста позволяет определить устойчивость замкнутой системы, построив частотную характеристику разомкнутой системы. Пусть $L(s)$ – передаточная функция разомкнутой системы, а $L(jω)$ – ее частотная характеристика.

Для простоты сначала будем считать, что разомкнутая система устойчива и не содержит интегрирующих звеньев, то есть $L(0)=K≠∞$, где $K$ – некоторое число.
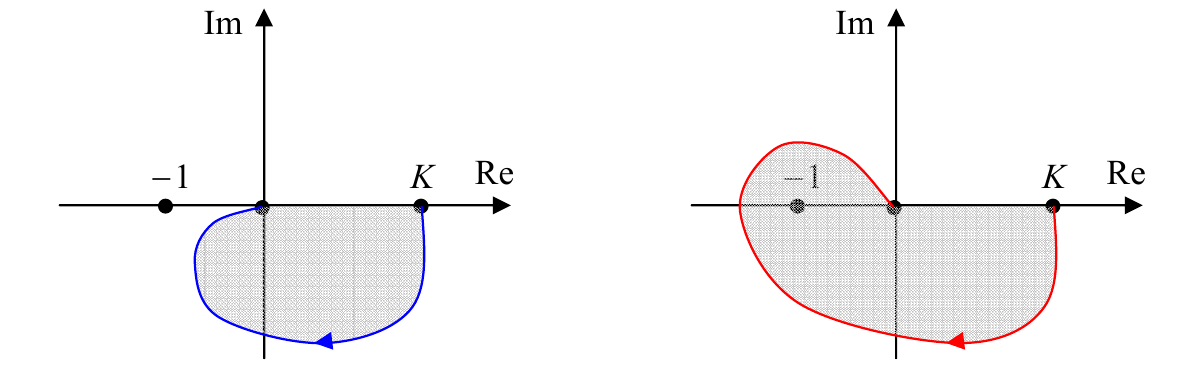
Для каждой частоты $ω$ значение $L(jω)$ – это комплексное число, которое можно изобразить точкой на комплексной плоскости. При изменении частоты от 0 до ∞ из этих точек складывается годограф Найквиста – некоторая кривая, которая начинается в точке ($K$;$0$) на вещественной оси и заканчивается в начале координат (если $L(s)$ – строго правильная функция, то есть степень ее числителя меньше степени знаменателя). Можно доказать, что система устойчива тогда и только тогда, когда годограф $L(jω)$ не охватывает точку ($−1$;$0$). На рисунке слева годограф не охватывает эту точку (и замкнутая система устойчива), а на рисунке справа – охватывает (система неустойчива).
Выражение «система находится на границе устойчивости» означает, что частотная характеристика проходит через точку ($−1$;$0$). В этом случае для некоторой частоты ω мы имеем $A(ω)=1$ и $φ(ω)=-180°$. Это говорит о том, что после прохождения контура величина сигнала меняет знак, сохраняя абсолютную величину (энергию), то есть устанавливаются незатухающие колебания.
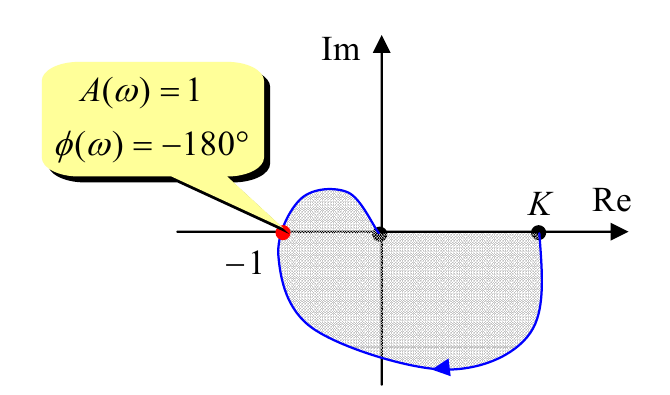
Частота $ω_c$, для которой $A(ω_c)=1$, называется частотой среза. Для устойчивой системы значение фазы на частоте среза должно быть больше, чем $−180°$; в этом случае годограф не охватит точку ($−1$;$0$).
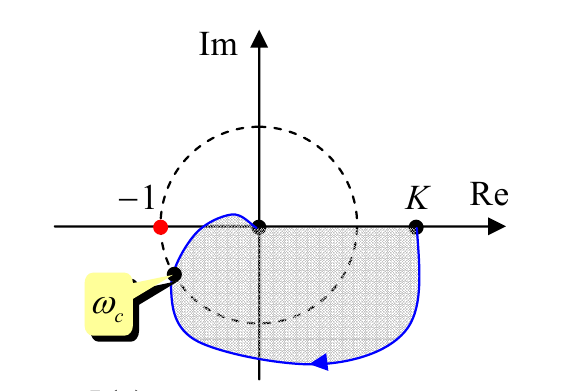
Если передаточная функция $L(s)$ имеет полюса в точке $s=0$ (то есть обращается в бесконечность в этой точке), ситуация усложняется. Теперь годограф начинается не на вещественной оси, а приходит из бесконечности. Тогда в контур необходимо включить не только полученную кривую, но и часть окружности бесконечного радиуса от вещественной оси до годографа в порядке обхода по часовой стрелке. Если функция $L(s)$ имеет $k$ полюсов в точке $s=0$, нужно добавить $k$ секторов по $90°$. На рисунках показаны годографы Найквиста устойчивых систем, в которых функция $L(s)$ имеет соответственно 1 и 2 полюса в точке $s=0$. Эти годографы не охватывают точку ($−1$; $0$).
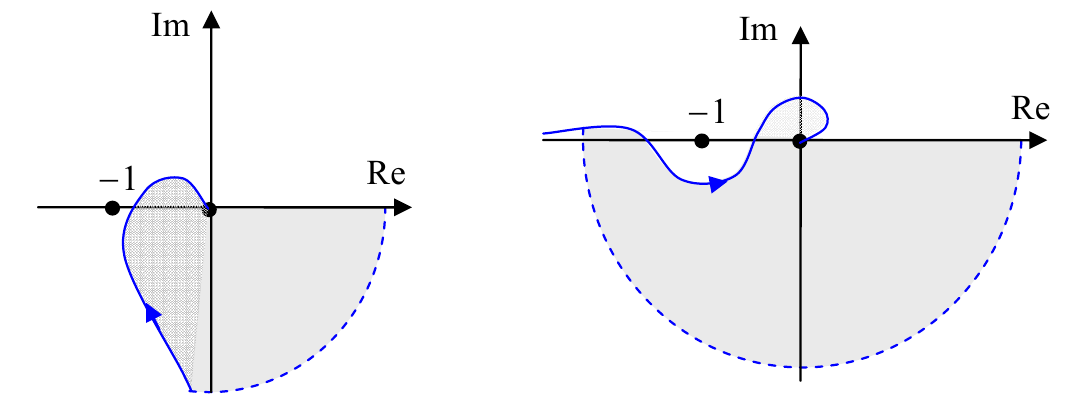
Если в системе есть запаздывание на время $τ$, на любой частоте появляется дополнительный сдвиг фазы на $-τω$ (без изменения амплитуды). Это значит, что каждая точка годографа поворачивается на некоторый угол против часовой стрелки.

На рисунке синяя линия – частотная характеристика системы без запаздывания, а красная – аналогичная характеристика для системы с запаздыванием. Видно, что запаздывание привело к неустойчивости системы (годограф охватил критическую точку ($−1$; $0$)).Таким образом, система может потерять устойчивость из-за «медленного» датчика. Можно говорить о том, что запаздывание всегда ухудшает устойчивость системы, и этот факт важно учитывать при проектировании.
Если $L(s)$ имеет полюса с положительной вещественной частью (разомкнутая система неустойчива), нужно считать, сколько раз годограф пересекает ось абсцисс левее точки ($−1$; $0$).
Причем переходы «сверху вниз» считаются положительными, а переходы «снизу вверх» – отрицательными.
Для того, чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы разница между числом положительных и отрицательных переходов была равна $l/2$, где $l$ – число неустойчивых полюсов функции $L(s)$. Начальная точка на оси абсцисс левее точки ($−1$; $0$) считается за половину перехода. На рисунке показаны годографы устойчивых систем для случая $l=1$.
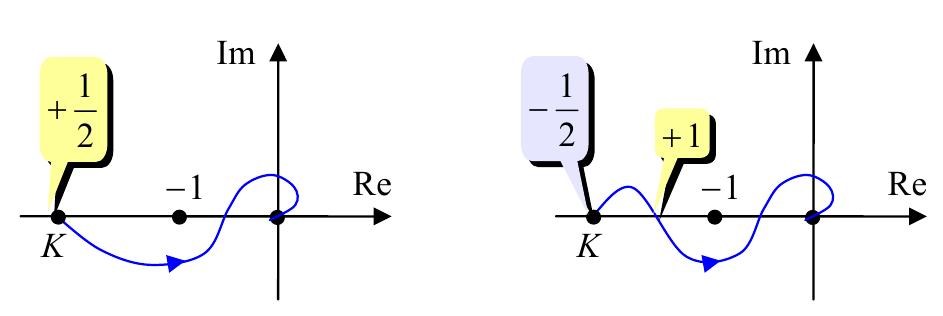
Частотная характеристика начинается на вещественной оси левее точки ($−1$; $0$). На рисунке слева годограф сначала идет вниз (половина положительного перехода) и больше нигде не пересекает ось абсцисс левее точки ($−1$; $0$), поэтому разница переходов равна $1/2=l/2$ и замкнутая система устойчива.
На правом рисунке частотная характеристика сначала идет вверх (считаем это за половину отрицательного перехода), а затем переходит в нижнюю полуплоскость (положительный переход). Разница снова равна $1/2=l/2$ и система устойчива.
Хорошо спроектированная система должна не только быть устойчивой и поддерживать заданную точность в установившемся режиме, но и плавно переходить на новый режим при изменении заданного значения выхода (уставки). Качество переходных процессов обычно оценивается по переходной характеристике (реакции системы на единичный ступенчатый входной сигнал).
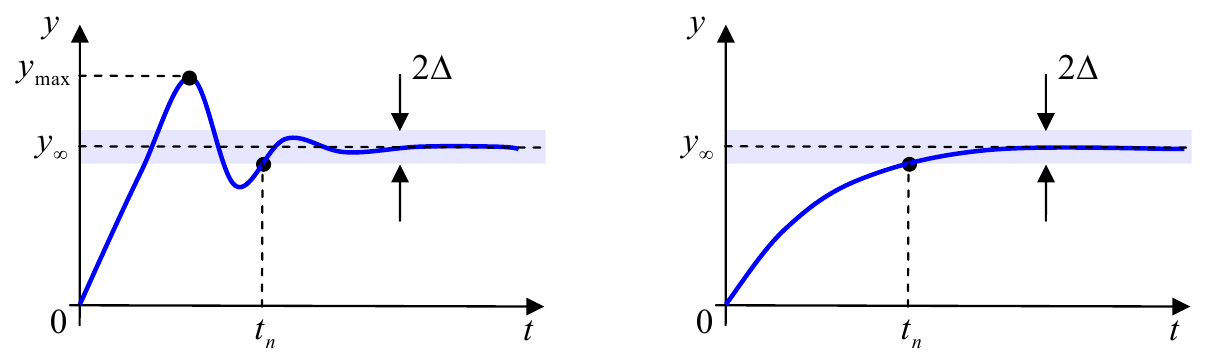
В первую очередь нас интересует, насколько быстро заканчивается переход на другой режим (время переходного процесса $t_п$). Оно определяется как время, через которое регулируемая величина «входит в коридор» шириной $2∆$ в округ установившегося значения $y_∞$. Это значит, что при $t>t_п$ значение выхода отличается от установившегося не более, чем на $∆$. Обычно величина $∆$ задается в процентах от установившегося значения, чаще всего 2% или 5%. Заметим, что для апериодического звена с постоянной времени $T$ время переходного процесса равно $t_п=3T$ (с точностью 5%).
Другая важная характеристика – перерегулирование $σ$ – показывает, на сколько процентов максимальное значение выхода $y_max$ превышает установившееся значение $y_∞$:
$$σ=\frac{y_max-y_∞}{y_∞}·100%.$$Иногда удается обеспечить нулевое перерегулирование (апериодический переходный процесс, как у апериодического звена). Нужно помнить, что увеличение быстродействия обычно приводит к увеличению перерегулирования.
Вы уже знаете, что устойчивость линейной системы определяется полюсами ее передаточной функции $W(s)$, однако на переходные процесс влияют и нули, причем в некоторых случаях очень существенно. Для примера рассмотрим передаточную функцию
$$W(s)=\frac{as+1}{(s+1)^2} = \frac{a(s+1/a)}{(s+1)^2} ,$$где $a$ может принимать как положительные, так и отрицательные значения.
Такая передаточная функция имеет нуль в точке $s=-1/a$. Нули, находящиеся в левой полуплоскости (при $a>0$) часто называют устойчивыми (по аналогии с полюсами), а нули в правой полуплоскости (при $a < 0$) – неустойчивыми. Очевидно, что при $a=0$ мы получаем апериодическое звено второго порядка. Теперь построим переходные характеристики этого звена при разных значениях $a$.
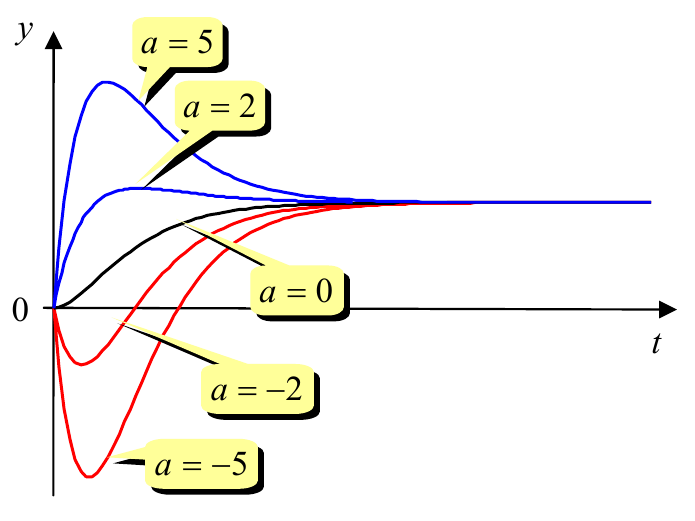
По графикам видно, что при нулевом значении $a$ переходный процесс – апериодический.
При $a>0$ (устойчивый нуль) наблюдается перерегулирование, причем оно тем больше, чем больше модуль $a$. При отрицательных значениях $a$ в переходном процессе есть недорегулирование. Это значит, что в первый момент времени регулируемая переменная начинает изменяться в сторону, противоположную заданному значению.