Обычно система управления состоит из отдельных блоков, каждый из которых описывается уравнениями низкого порядка (чаще всего – первого или второго). Для понимания работы системы в целом желательно хорошо представлять, как ведут себя ее отдельные элементы.
Звенья, имеющие конечный ненулевой коэффициент усиления постоянного сигнала, то есть $W(0)=k≠0$, называются позиционными. Это значит, что числитель и знаменатель передаточной функции имеют ненулевые свободные члены (постоянные слагаемые).
Простейшее позиционное звено – идеальный (безынерционный) усилитель. Его передаточная функция $W(s)=k$. Строго говоря, он не является динамическим звеном, поскольку изменение выхода происходит мгновенно, сразу вслед за изменением входа. При действии на вход единичного ступенчатого сигнала $1(t)$ (или дельта-функции $δ(t)$) на выходе будет такой же сигнал, усиленный в $k$ раз, поэтому переходная и импульсная характеристики звена равны
$$h(t)=k\ (t>0)$$и
$$w(t)=k·δ(t).$$Если на вход усилителя действует синусоидальный сигнал, на выходе он усиливается в $k$ раз без изменения фазы, поэтому амплитудная и фазовая частотная характеристики не зависят от частоты входного сигнала:
$$A(ω)=k,$$ $$φ(ω)=0.$$Одно из самых часто встречающихся звеньев – апериодическое, которое описывается дифференциальным уравнением
$$T \frac{\mathrm{d}y(t)}{\mathrm{d}t}+y(t)=k·x(t)$$и имеет передаточную функцию
$$W(s)=\frac{k}{Ts+1}.$$Здесь $k$ – безразмерный коэффициент, а $T>0$ – постоянная, которая называется постоянной времени звена. Постоянная времени – размерная величина, она измеряется в секундах и характеризует инерционность объекта, то есть скорость его реакции на изменение входного сигнала.
Мы уже нашли переходную и весовую функции апериодического звена
$$h(t)=k·\left(1-exp\left(\frac{-t}{T}\right)\right),$$ $$w(t)=\frac{k}{T}·exp\left(\frac{-t}{T}\right).$$Они показаны на рисунке:
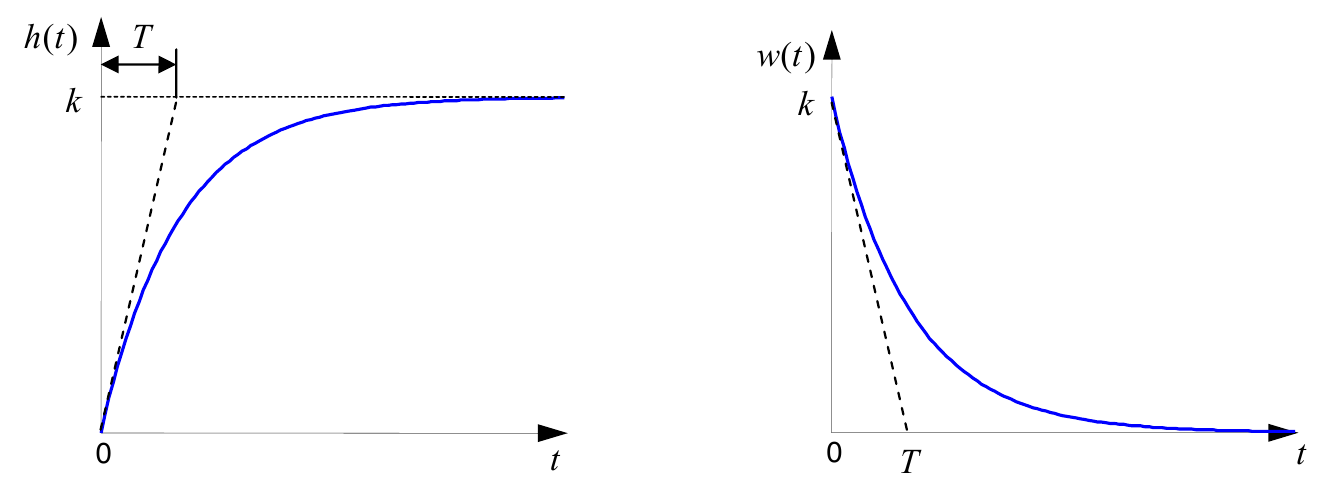
Обратите внимание, что предельное значение переходной характеристики равно $k$, а касательная к ней в точке $t=0$ пересекается с линией установившегося значения при $t=T$. Переходная и импульсная характеристики выходят на установившееся значение (с ошибкой не более 5%) примерно за время $3T$ . Эти факты позволяют определять постоянную времени экспериментально, по переходной характеристике звена.
Частотная характеристика определяется выражением
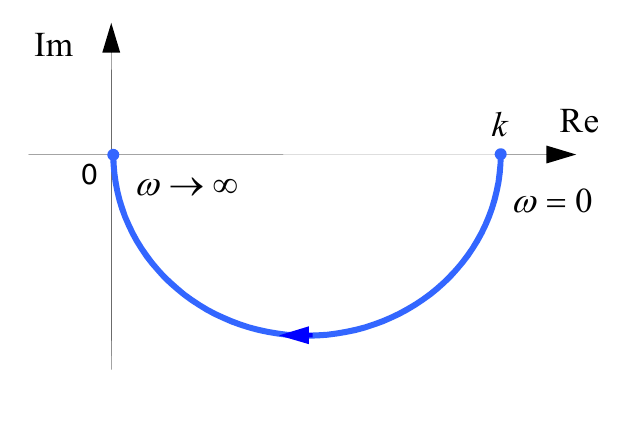
$$W(jω)=\frac{k}{Tjω+1}=\frac{k·(1-Tjω)}{(Tjω+1)(1-Tjω)}=\frac{k}{T^2 ω^2+1}-\frac{jkTω}{T^2 ω^2+1}.$$Для каждой частоты ω значение $W(jω)$ – это точка на комплексной плоскости. При изменении $ω$ от $0$ до $∞$ получается кривая, которая называется годографом Найквиста (диаграммой Найквиста). В данном случае можно показать, что частотная характеристика – это полуокружность с центром в точке ($0.5k$; $0$) радиуса $0.5k$. Годограф начинается (на нулевой частоте) в точке ($k$; $0$) и заканчивается в начале координат (при $ω→∞$).
Для сравнения рассмотрим также неустойчивое апериодическое звено, которое задается уравнением
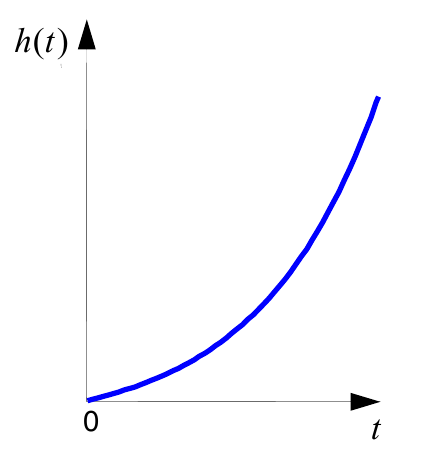
$$T \frac{\mathrm{d}y(t)}{\mathrm{d}t}-y(t)=k·x(t).$$Как видим, все отличие только в знаке в левой части уравнения (плюс сменился на минус). Однако при этом кардинально меняются переходная и импульсная характеристики:
$$h(t)=k·\left(exp\left(\frac{t}{T}\right)-1\right),$$ $$w(t)=\frac{k}{T}·exp\left(\frac{t}{T}\right).$$Обычно предполагается, что постоянная времени $T>0$, тогда экспоненты в этих выражениях бесконечно возрастают с ростом $t$.
Поэтому звено названо «неустойчивым»: в покое оно находится в неустойчивом равновесии, а при малейшем возмущении «идет вразнос».
Колебательное звено – это звено второго порядка с передаточной функцией вида
$$W(s)=\frac{k}{b_2 s^2+b_1 s+1},$$знаменатель которой имеет комплексно-сопряженные корни (то есть, $b_1^2-2b_2< 0$). Как известно из теории дифференциальных уравнений, свободное движение такой системы содержит гармонические составляющие (синус, косинус), что дает колебания выхода при изменении входного сигнала.
Несложно представить передаточную функцию колебательного звена в форме
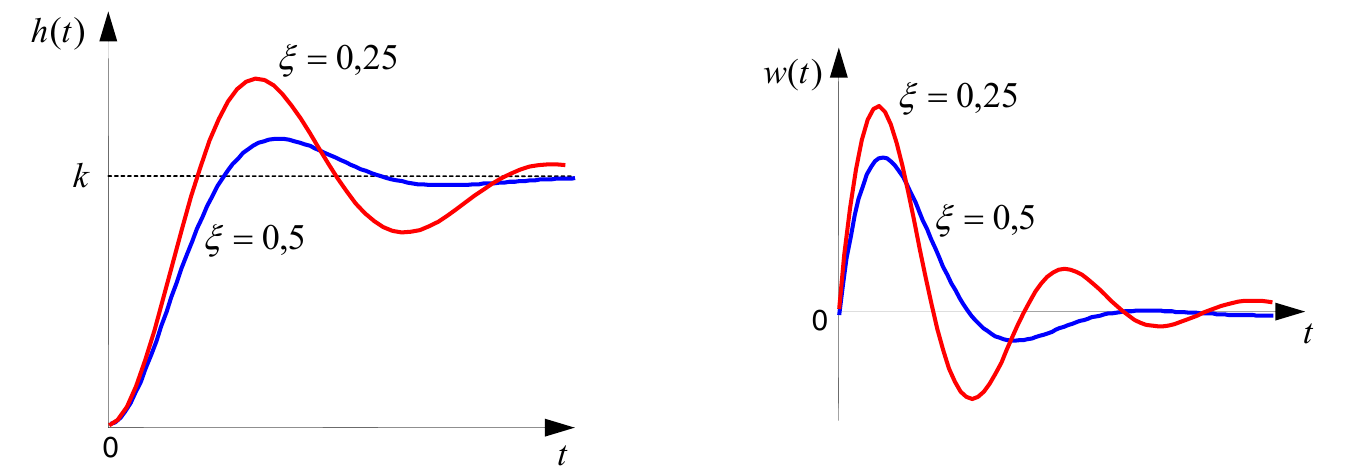
$$W(s)=\frac{k}{T^2 s^2+2Tξs+1},$$где $k$ – коэффициент, $T$ – постоянная времени (в секундах), $ξ$ – параметр затухания ($0 < ξ < 1$). Постоянная времени определяет инерционность объекта, чем она больше, тем медленнее изменяется выход при изменении входа. Чем больше $ξ$, тем быстрее затухают колебания.
При $ξ=0$ получается консервативное звено, которое дает незатухающие колебания на выходе. Если $ξ≥1$, модель представляет апериодическое звено второго порядка, то есть последовательное соединение двух апериодических звеньев.
Колебательное звено относится к позиционным звеньям, его статический коэффициент усиления равен $W(0)=k$.
Переходная и импульсная характеристики отличаются выраженной колебательностью, особенно при малых значениях параметра затухания $ξ$. На следующих двух графиках синие линии соответствуют $ξ=0.5$, а красные – $ξ=0.25$.
Простейший пример интегрирующего звена – ванна, в которую набирается вода. Входной сигнал – это поток воды через кран, выход системы – уровень воды в ванне. При поступлении воды уровень растет, система «накапливает» (интегрирует) входной сигнал.
Интегрирующее звено описывается уравнением
$$\frac{\mathrm{d}y(t)}{\mathrm{d}t}=k·x(t),$$которому соответствует передаточная функция
$$W(s)=\frac{k}{s}.$$Решение уравнения дает
$$y(t)=y(0)+k∫_0^t x(τ)\mathrm{d}τ.$$Используя это решение для единичного скачка ($x(t)=1$ при $t≥0$) при нулевых начальных условиях ($y(0)=0$), получаем линейно возрастающую переходную характеристику:
$$h(t)=k·t.$$Для того, чтобы найти импульсную характеристику, вспомним, что интеграл от дельта-функции на любом интервале, включающем $t=0$, равен $1$. Поэтому $w(t)=k$ (при $t≥0$).
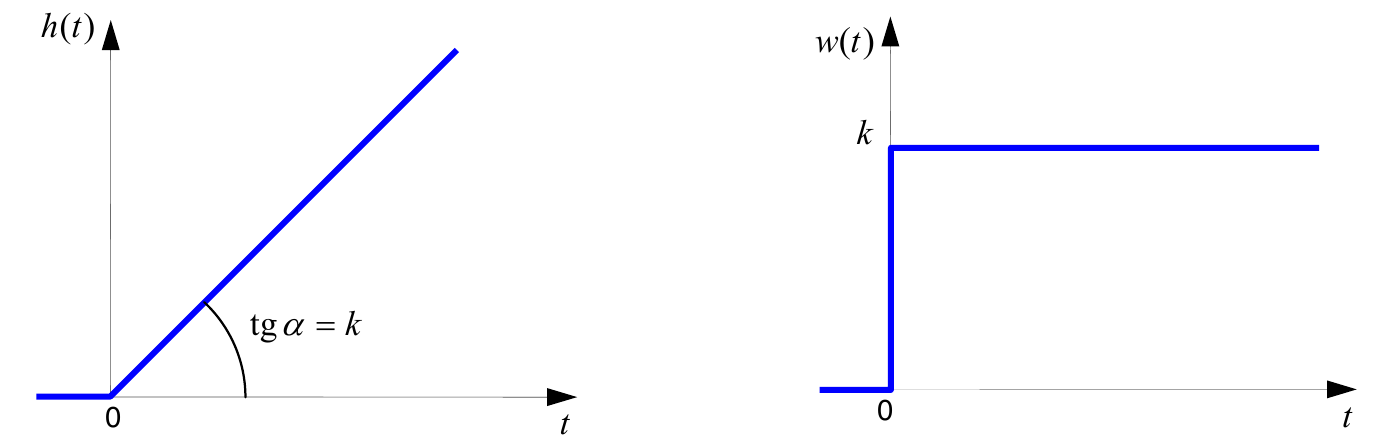
Частотная характеристика интегрирующего звена определяется формулой
$$W(jω)=\frac{k}{jω}=-j·\frac{k}{ω}.$$Дифференцирующее звено дает на выходе производную входного сигнала. Уравнение идеального дифференцирующего звена
$$y(t)=k \frac{\mathrm{d}x(t)}{\mathrm{d}t},$$его операторная запись
$$y(t)=k·p\ x(t),$$передаточная функция
$$W(s)=k·s.$$Это физически нереализуемые функции, так как дельта-функцию и ее производную, имеющие бесконечные значения, невозможно получить на реальном устройстве. Поэтому идеальное дифференцирующее относится к физически нереализуемым звеньям.
Дифференцирующее звено реагирует не на изменение самой входной величины, а на изменение ее производной, то есть на тенденцию развития событий. Поэтому говорят, что дифференцирующее звено обладает упреждающим, прогнозирующим действием. С его помощью можно ускорить реакцию системы.
В технике не могут использоваться физически нереализуемые звенья. Поэтому важно рассмотреть аналогичное звено, которое выполняет дифференцирования низкочастотных сигналов и одновременно имеет ограниченное усиление на высоких частотах. Инерционное дифференцирующее звено описывается уравнением
$$T \frac{\mathrm{d}y(t)}{\mathrm{d}t}+y(t)=k·\frac{\mathrm{d}x(t)}{\mathrm{d}t}$$и имеет передаточную функцию
$$W(s)=\frac{ks}{Ts+1}.$$Фактически это последовательное соединение идеального дифференцирующего и апериодического звеньев.
Апериодическое звено добавляет инерционность: обладая свойствами фильтра низких частот, оно ограничивает усиление на высоких частотах. Поскольку передаточная функция имеет равные степени числителя и знаменателя, на высоких частотах.
Представим себе трубу, через которую вентилятор прокачивает воздух. В начале трубы установлен нагреватель, а температура воздуха измеряется датчиком в точке $А$.
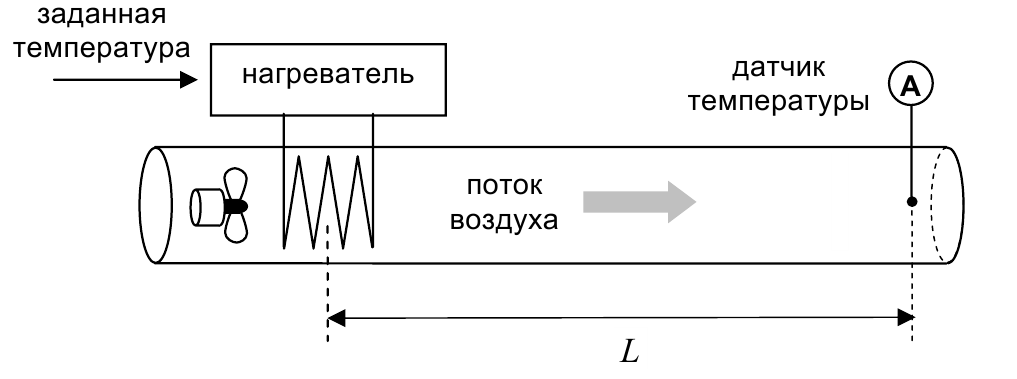
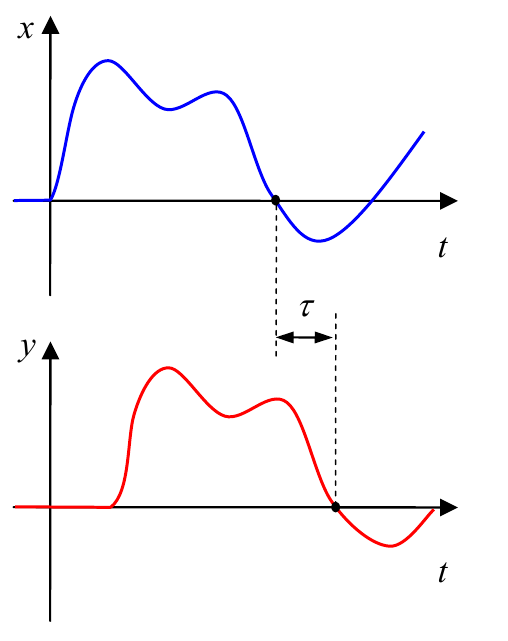
Очевидно, что при изменении температуры воздуха датчик обнаружит это не сразу, а через время $τ=L/v$, где $L$ – длина трубы (в метрах), а $v$ – скорость потока воздуха (в м/с). В этом случае говорят, что в системе есть транспортное запаздывание на величину $τ$ (в секундах).
Другой распространенный пример – вычислительное запаздывание в компьютере. Так называется время, которое необходимо для расчета нового управляющего сигнала после получения всех исходных данных.
Запаздывание в системе просто сдвигает сигнал вправо на временной оси, не меняя его формы. Математически это можно записать в виде
$$y(t)=x(t-τ)$$Изображение сигнала на выходе звена запаздывания вычисляется по теореме о смещении аргумента для преобразования Лапласа:
$$Y(s)=\mathscr{L}\{y(t)\}=∫_0^∞ x(t-τ)·e^{-s·t} \mathrm{d}t=e^{-s·τ} X(s),$$поэтому передаточная функция звена чистого запаздывания равна
$$W(s)=e^{-s·τ}.$$Очевидно, что при гармоническом входном сигнале запаздывание не изменяет амплитуду, но вносит дополнительный отрицательный сдвиг фазы. Частотная характеристика этого звена имеет вид
$$W(jω)=e^{-jω·τ}.$$По общим формулам находим:
$$A(jω)=|W(jω)|=1,$$ $$φ(jω)=arg(W(jω))=-ωτ.$$Таким образом, фазовая частотная характеристика звена запаздывания – линейная функция частоты $ω$ , чем больше частота, тем больше фазовый сдвиг.