Составляя модель объекта на основании физических законов, мы чаще всего получаем систему дифференциальных уравнений первого и второго порядка.
Для примера покажем, как построить модель двигателя постоянного тока, используя законы механики и электротехники. Вход этого объекта – напряжение якоря $u(t)$ (в вольтах), выход – угол поворота вала $θ(t)$ (в радианах).
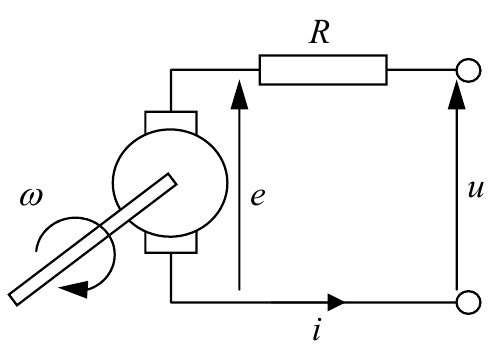
Вал двигателя начинает вращаться, когда приложено напряжение питания. Если напряжение не меняется, угловая скорость вращения $ω(t)$ (в радианах в секунду) остается постоянной, при этом угол $θ(t)$ равномерно увеличивается.
Чем больше напряжение, тем быстрее вращается вал. Если подключить нагрузку, например, заставить двигатель вращать турбину, скорость вращения постепенно уменьшается до нового значения, при котором вращающий момент двигателя будет равен моменту сопротивления (нагрузки). Пока эти моменты равны, скорость вращения остается постоянной и ее производная равна нулю.
Теперь переведем эти рассуждения на строгий язык математики. Угловая скорость вращения $ω(t)$ вычисляется как производная от угла поворота вала $θ(t)$, то есть
$$ω(t)=\frac{\mathrm{d}θ(t)}{\mathrm{d}t}.$$Соответственно, угол $θ(t)$ – это интеграл от угловой скорости. В механике уравнение вращательного движения обычно записывают в виде
$$J \frac{\mathrm{d}ω(t)}{\mathrm{d}t} = M(t)-M_н (t),$$где $M(t)$ – вращающий момент (измеряется в H·м), $M_н (t)$ – момент нагрузки (возмущение, также в H·м). Буквой $J$ обозначен суммарный момент инерции якоря и нагрузки (в кг·м2). Величина момента инерции говорит о том, насколько легко «разогнать» двигатель (чем больше момент инерции, тем сложнее «разогнать»).
Перейдем к электротехнике. В нашем случае момент $M(t)$ – это электромагнитный момент двигателя, который вычисляется по формуле
$$M(t) = C_м·Ф·i(t),$$где $C_м$ – коэффициент, $Ф$ – магнитный поток, создаваемый обмоткой возбуждения (измеряется в веберах); $i(t)$ – ток якоря (в амперах), который может быть найден из уравнения
$$u(t)=e(t)+R·i(t),$$где $e(t)$ – электродвижущая сила (ЭДС) якоря (в вольтах) и $R$ – сопротивление якорной цепи (в омах). В свою очередь, ЭДС рассчитывается через магнитный поток и частоту вращения:
$$e(t)=C_ω·Ф·ω(t),$$где $C_ω$ – коэффициент. Вводя новые постоянные $k_1=C_м·Ф$ и $k_2=C_ω·Ф$, можно записать модель двигателя в виде системы уравнений
$$J \frac{\mathrm{d}ω(t)}{\mathrm{d}t}=k_1·i(t)-M_н (t),$$ $$e(t)=k_2·ω(t),$$ $$ω(t)=\frac{\mathrm{d}θ(t)}{\mathrm{d}t},$$ $$u(t)=e(t)+R·i(t).$$Модель описывает связи реальных сигналов в системе, ее внутреннее устройство.
Часто нам достаточно знать, как будет реагировать объект на заданный входной сигнал (управление). При этом его внутреннее устройство нас не очень интересует, то есть мы рассматриваем объект в качестве «черного ящика». Переходя к переменной $θ(t)$, получаем:
$$J \frac{\mathrm{d^2}θ(t)}{\mathrm{d}t^2} =\frac{k_1}{R}·\left [u(t)-k_2·\frac{\mathrm{d}θ(t)}{\mathrm{d}t} \right]-M_н (t),$$или, перенося все члены, зависящие от $θ(t)$, в левую часть равенства
$$J \frac{\mathrm{d^2}θ(t)}{\mathrm{d}t^2} + \frac{k_1·k_2}{R}·\frac{\mathrm{d}θ(t)}{\mathrm{d}t} = \frac{k_1}{R}·u(t)-M_н (t),$$Это дифференциальное уравнение второго порядка, связывающее вход $u(t)$ и нагрузку $M_н (t)$ с выходом $θ(t)$. В сравнении с системой, все внутренние сигналы исходной модели $e(t)$ и $i(t)$ были исключены из уравнений. Поэтому последнее уравнение называется уравнением «вход-выход».
Порядком модели называют порядок соответствующего дифференциального уравнения. В данном случае мы получили модель второго порядка.
В этом разделе на простом примере рассмотрено, как на основе физических законов строятся математические модели объектов управления. Как правило, они представляют собой дифференциальные уравнения.
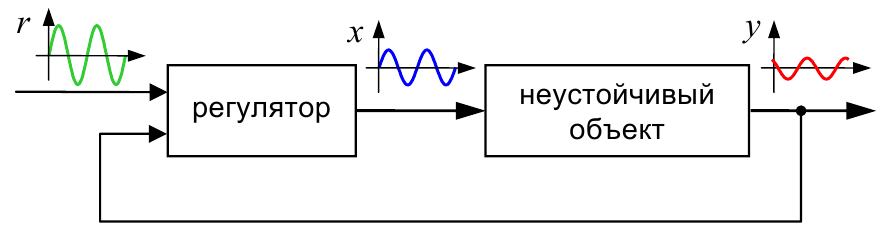
Для того, чтобы было легче исследовать модель объекта, желательно привести ее к некоторому стандартному виду, для которого уже есть готовые общие решения. Таким «стандартом» в теории управления считается система дифференциальных уравнений первого порядка, которая называется нормальной формой Коши.
Рассмотрим снова модель электродвигателя, считая, что $M_н (t)=0$ (нагрузки нет). Вспомнив, что $ω(t)=\frac{\mathrm{d}θ(t)}{\mathrm{d}t}$, можно записать
$$\frac{\mathrm{d}ω(t)}{\mathrm{d}t}=-\frac{k_1·k_2}{J·R}·ω(t)+\frac{k_1}{J·R}·u(t).$$Эта система дифференциальных уравнений первого порядка быть записана в матричной форме:
$$\begin{bmatrix}\frac{\mathrm{d}θ(t)}{\mathrm{d}t}\\\frac{\mathrm{d}ω(t)}{\mathrm{d}t}\end{bmatrix} = \begin{bmatrix}0&1\\0&-\frac{k_1·k_2}{J·R}\end{bmatrix}· \begin{bmatrix}θ(t)\\ω(t)\end{bmatrix} + \begin{bmatrix}0\\\frac{k_1}{J·R}\end{bmatrix}·u(t)$$Значения $θ(t)$ и $ω(t)$ определяют состояние двигателя в момент времени $t$. Это значит, что зная их значения в некоторый момент времени $t_0$ и входной сигнал $u(t)$ при всех $t≥t_0$ можно рассчитать поведение объекта для любого последующего момента. При этом предыдущие значения $θ(t)$, $ω(t)$ и $u(t)$ (при $t < t_0$) не играют никакой роли. Поэтому $θ(t)$ и $ω(t)$ называются переменными состояния, а вектор $\begin{bmatrix}θ(t)\\ω(t)\end{bmatrix}$ – вектором состояния.
В теории управления принято обозначать вектор состояния через $x(t)$, вход объекта (сигнал управления) – через $u(t)$. Тогда модель может быть записана в виде
$$\frac{\mathrm{d}x(t)}{\mathrm{d}t}=A·x(t)+B·u(t),$$где $x(t)=\begin{bmatrix}θ(t)\\ω(t)\end{bmatrix}$, $A=\begin{bmatrix}0&1\\0&-\frac{k_1·k_2}{J·R}\end{bmatrix}$ и $B=\begin{bmatrix}0\\\frac{k_1}{J·R}\end{bmatrix}$. Модель связывает вход $u(t)$ и вектор состояния $x(t)$, поэтому она называется моделью вход-состояние.
Полная модель объекта в пространстве состояний содержит еще одно уравнение – уравнение выхода, которое показывает, как формируется выход объекта $y(t)$:
$$\frac{\mathrm{d}x(t)}{\mathrm{d}t}=A·x(t)+B·u(t),$$ $$y(t)=C·x(t)+D·u(t).$$Эта модель называется моделью вход-состояние-выход. Выходная координата для двигателя постоянного тока – это угол поворота вала:
$$y(t) = θ(t) = \begin{bmatrix}1&0\end{bmatrix}·\begin{bmatrix}θ(t)\\ω(t)\end{bmatrix} = \begin{bmatrix}1&0\end{bmatrix}·x(t),$$так что $C=\begin{bmatrix}1&0\end{bmatrix}$ и $D=0$. Если же в качестве выхода принять угловую скорость, то $C=\begin{bmatrix}0&1\end{bmatrix}$.
С помощью последней модели, изменяя матрицы $C$ и $D$, можно принять за выход любую линейную комбинацию переменных состояния и входа. Во многих практических задачах выход – это одна или несколько переменных состояния, которые мы можем измерить.
Поскольку момент инерции $J$, сопротивление якоря $R$ и коэффициенты $k_1$ и $k_2$ не зависят от времени, матрицы $A$, $B$, $C$ и $D$ в модели – постоянные. Такие объекты называются стационарными, в отличие от нестационарных объектов, параметры которых изменяются во времени.
Запись моделей в единой форме позволяет отвлечься от смысла переменных состояния и исследовать системы разной природы стандартными методами, которые хорошо разработаны и реализованы в современных компьютерных программах.
Покажем, как данные уравнения могут быть решены и чем удобна именно такая форма записи. Предположим, что мы знаем начальные условия, то есть вектор состояния $x(0)$ при $t=0$. Вспомним, что знание $x(0)$ и входа $u(t)$ при всех $t>0$ дает возможность однозначно определить дальнейшее поведение этого объекта.
Первое уравнение в системе позволяет найти производную, то есть, скорость изменения вектора состояния $x(t)$ в любой момент времени. Будем считать, что при $0≤t≤∆t$, где $∆t$ – малый интервал времени, эта производная не меняется. Тогда значение вектора состояния при $t=∆t$ приближенно определяется формулой
$$x(∆t)≈x(0)+\frac{\mathrm{d}x(0)}{\mathrm{d}t}·∆t=x(0)+(A·x(0)+B·u(0))·∆t,$$то есть, его можно легко вычислить. Зная $x(∆t)$ и сигнал управления $u(∆t)$, находим выход системы в тот же момент
$$y(∆t)≈C·x(∆t)+D·u(∆t).$$Эту методику можно применять и дальше, в конце второго интервала получаем
$$x(2·∆t)≈x(∆t)+\frac{\mathrm{d}x(∆t)}{\mathrm{d}t}·∆t=x(∆t0)+(A·x(∆t)+B·u(∆t))·∆t,$$ $$y(2·∆t)≈C·x(2·∆t)+D·u(2·∆t).$$Таким образом, можно (приближенно) рассчитать выход системы при всех $t>0$. Конечно, точность будет тем выше, чем меньше $∆t$, однако объем вычислений при этом также увеличится.
Этот метод приближенного решения дифференциальных уравнения называется методом Эйлера.
Выходной сигнал системы можно представить как результат действия некоторого оператора на ее вход. Для линейных моделей такой оператор можно записать следующим образом.
Пусть модель объекта задана линейным дифференциальным уравнением второго порядка, связывающим вход $x(t)$ и выход $y(t)$:
$$b_2 \frac{\mathrm{d^2}y(t)}{\mathrm{d}t}^2 +b_1 \frac{\mathrm{d}y(t)}{\mathrm{d}t}+b_0 y(t)=a_1 \frac{\mathrm{d}x(t)}{\mathrm{d}t}+a_0 x(t),$$где $a_i (i=0,1)$ и $b_i (i=0,1,2)$ – постоянные. Введем оператор дифференцирования $p=\frac{\mathrm{d}}{\mathrm{d}t}$, который действует на сигнал $x(t)$ по правилу $p\ x(t)=\frac{\mathrm{d}x(t)}{\mathrm{d}t}$. Обратите внимание, что запись $p\ x(t)$ обозначает не умножение оператора $p$ на $x(t)$, а действие этого оператора, то есть дифференцирование $x(t)$.
Теперь запишем производные сигналов $x(t)$ и $y(t)$ по времени в операторной форме
$$\frac{\mathrm{d}y(t)}{\mathrm{d}t}=p\ y(t),$$ $$\frac{\mathrm{d^2}y(t)}{\mathrm{d}t^2} =p^2\ y(t),$$ $$\frac{\mathrm{d}x(t)}{\mathrm{d}t}=p\ x(t).$$Подставляя эти выражения, получим
$$b_2 p^2\ y(t)+b_1 p\ y(t)+b_0 y(t)=a_1 p\ x(t)+a_0 x(t).$$Можно формально вынести за скобки $y(t)$ в левой части равенства и $x(t)$ в правой части:
$$(b_2 p^2+b_1 p+b_0 )y(t)=(a_1 p+a_0 )x(t).$$Левая часть означает, что оператор $b_2 p^2+b_1 p+b_0$ действует на сигнал $y(t)$, а в правой части оператор $a_1 p+a_0$ действует на сигнал $x(t)$. «Разделив» (условно, конечно) обе части на оператор $b_2 p^2+b_1 p+b_0$, связь выхода и входа можно записать в виде
$$y(t)=\frac{a_1 p+a_0}{b_2 p^2+b_1 p+b_0}\ x(t)=W(p)·x(t),$$где запись $W(p)·x(t)$ означает не умножение, а действие сложного оператора
$$W(p)=\frac{a_1 p+a_0}{b_2 p^2+b_1 p+b_0}$$на сигнал $x(t)$. Иначе говоря, формула $y(t)=W(p)·x(t)$ – это не что иное, как символическая запись, которую удобно использовать.
Функция $W(p)$ называется передаточной функцией объекта. Она полностью описывает связи между выходом и входом объекта при нулевых начальных условиях, но не учитывает его внутреннее устройство.
Часто передаточной функцией называют функцию $W(λ)$, которая получается в результате замены оператора $p$ на некоторую независимую переменную $λ$. Эта фукнция представляет собой отношение двух полиномов (многочленов) от $λ$.
Передаточная функция $W(λ)$ называется правильной, если степень ее числителя не больше, чем степень знаменателя; строго правильной, если степень числителя меньше степени знаменателя; неправильной, если степень числителя больше, чем степень знаменателя. Например, функция $\frac{1}{λ+1}$ – строго правильная и одновременно правильная; $\frac{λ}{λ+1}$ – правильная, но не строго правильная (иногда такие функции называют биправильными), а $\frac{λ^2+λ+1}{λ+1}$ – неправильная.
Нулями передаточной функции называются корни ее числителя, а полюсами – корни знаменателя. Например, функция
$$W(λ)=\frac{λ-1}{λ^2+3λ+2}$$имеет нуль в точке $λ=1$ и два полюса в точках $λ=-1$ и $λ=-2$.
Одна из первых задач, которые были поставлены в теории управления – вычисление выхода системы при известном входе. Мы видели, что для ее решения нужно решать дифференциальные уравнения. Чтобы упростить процедуру, математики придумали преобразование, которое позволило заменить решение дифференциальных уравнений алгебраическими вычислениями, то есть, операциями с полиномами (многочленами) и рациональными функциями.
Для функции $f(t)$ вводится преобразование Лапласа, которое обозначается как $\mathscr{L}\{f(t)\}$:
$$F(s)=\mathscr{L}\{f(t)\}=∫_0^∞ f(t)e^{-s·t} \mathrm{d}t.$$Функция $F(s)$ называется изображением для функции $f(t)$ (оригинала). Здесь $s$ – это комплексная переменная, которая выбирается так, чтобы интеграл сходился.
Обратное преобразование Лапласа $\mathscr{L}^{-1} \{f(t)\}$ позволяет вычислить оригинал $f(t)$ по известному изображению $F(s)$:
$$f(t)=\mathscr{L}^{-1} \{f(t)\}=\frac{1}{2πj} ∫_{σ-j∞}^{σ+j∞}F(s)e^{s·t} \mathrm{d}s,$$где $j=\sqrt{-1}$, а постоянная σ выбирается так, чтобы интеграл сходился.
На практике вместо интеграла чаще всего используют готовые таблицы, по которым можно сразу определить изображение по оригиналу и наоборот. Например, изображения по Лапласу для дельта-функции, единичного скачка и функции $e^{-a·t}$ равны, соответственно
$$\mathscr{L}\{δ(t)\}=1,$$ $$\mathscr{L}\{1(t)\}=\frac{1}{s},$$ $$\mathscr{L}\{e^{-a·t}\}=\frac{1}{s+a}.$$Преобразование Лапласа имеет несколько замечательных свойств. Во-первых, легко доказать, что принцип суперпозиции выполняется как для прямого, так и для обратного преобразования Лапласа:
$$\mathscr{L}\{f_1 (t)+f_2 (t)\}=\mathscr{L}\{f_1 (t)\}+\mathscr{L}\{f_2 (t)\},$$ $$\mathscr{L}^{-1} \{F_1 (s)+F_2 (s)\}=\mathscr{L}^{-1} \{F_1 (s)\}+\mathscr{L}^{-1} \{F_2 (s)\}.$$Во-вторых, изображение для производной функции $f(t)$ равно
$$\mathscr{L}\left \{\frac{\mathrm{d}f(t)}{\mathrm{d}t}\right \}=s·F(s)-f(0),$$где $F(s)$ – изображение функции $f(t)$, и $f(0)$ – ее значение при $t=0$. Поэтому при нулевых начальных условиях изображение производной равно изображению самой функции, умноженному на $s$. Аналогично для построения изображения i-ой производной нужно умножить изображение функции на $s^i$ (это также справедливо только при нулевых начальных условиях).
Кроме того, с помощью преобразование Лапласа можно сразу найти начальное и конечное значения функции-оригинала (при $t=0$ и $t→∞$), не вычисляя самого оригинала:
$$f(0)= \lim_{s\to ∞} s·F(s),$$ $$f(∞)= \lim_{s\to 0} s·F(s).$$Рассмотрим снова уравнение
$$b_2 \frac{\mathrm{d^2}y(t)}{\mathrm{d}t^2} +b_1 \frac{\mathrm{d}y(t)}{\mathrm{d}t}+b_0 y(t) = a_1 \frac{\mathrm{d}x(t)}{\mathrm{d}t}+a_0 x(t).$$Применим к левой и правой частям преобразование Лапласа, считая, что все начальные условия нулевые. Получается уравнение в изображениях, связывающее преобразования Лапласа входа $X(s)$ и выхода $Y(s)$:
$$b_2 s^2 Y(s)+b_1 sY(s)+b_0 Y(s)=a_1 sX(s)+a_0 X(s).$$Можно вынести за скобки $Y(s)$ в левой части и $X(s)$ в правой части:
$$(b_2 s^2+b_1 s+b_0 )Y(s)=(a_1 s+a_0 )X(s).$$Разделив обе части этого равенства на $b_2 s^2+b_1 s+b_0$, получаем
$$Y(s)=(a_1 s+a_0)/(b_2 s^2+b_1 s+b_0 ) X(s)=W(s)·X(s).$$$W(s)$ – это передаточная функция объекта, записанная в виде функции от комплексной переменной $s$, а не от оператора дифференцирования $p$.
Таким образом, при нулевых начальных условиях изображение выхода линейного объекта вычисляется как произведение его передаточной функции на изображение входного сигнала.
Из этого следует и другой важный вывод: передаточная функция равна отношению изображений по Лапласу выхода и входа при нулевых начальных условиях.
Рассмотрим пример использования преобразования Лапласа для вычисления выхода системы при известном входном сигнале. Пусть объект управления описывается уравнением первого порядка:
$$T \frac{\mathrm{d}y(t)}{\mathrm{d}t}+y(t)=k·x(t),$$и на его вход поступает единичный ступенчатый сигнал $x(t)=1(t)$. Требуется найти сигнал выхода $y(t)$, который в данном случае представляет собой переходную характеристику.
Решим эту задачу с помощью передаточных функций и изображений сигналов по Лапласу. Чтобы найти изображение выхода, нужно знать изображение входного сигнала $X(s)$ и передаточную функцию звена $W(s)$. Изображения находим по табличным данным, повторяя приведенные выше рассуждения:
$$X(s)=\frac{1}{s},$$ $$W(s)=\frac{k}{Ts+1}.$$Теперь находим изображение выхода
$$Y(s)=\frac{1}{s}·\frac{k}{Ts+1}.$$Вычисляем оригинал – сигнал выхода:
$$y(t)=\mathscr{L}^{-1} \{Y(s)\}=\mathscr{L}^{-1}\left \{\frac{1}{s}·\frac{k}{Ts+1}\right \}.$$Обратное преобразования Лапласа:
$$y(t)=-k·\left (exp\left (\frac{-t}{T}\right )-1\right ).$$Таким способом можно вычислять реакцию системы на известный входной сигнал без прямого решения дифференциального уравнения.
Вычислим начальное и конечное значение сигнала выхода $y(t)$:
$$y(0)=\lim_{s\to ∞} s·Y(s)=0,$$ $$y(∞)=\lim_{s\to 0} s·Y(s)=k.$$Значение $W(0)$ называют статическим коэффициентом усиления звена, поскольку он показывает, во сколько раз усиливается постоянный сигнал.
Один из методов построения моделей «вход-выход» – определение реакции объекта на некоторый стандартный сигнал. Один из простейших сигналов – так называемый «единичный скачок» («единичный ступенчатый сигнал»), то есть мгновенное изменение входного сигнала с 0 до 1 в момент $t=0$. Формально этот сигнал определяется так:
$$1(t)=\begin{cases} 0,t < 0\\1, t ≥ 0\end{cases}.$$Реакция объекта на единичный скачок называется переходной функцией и обозначается $h(t)$.
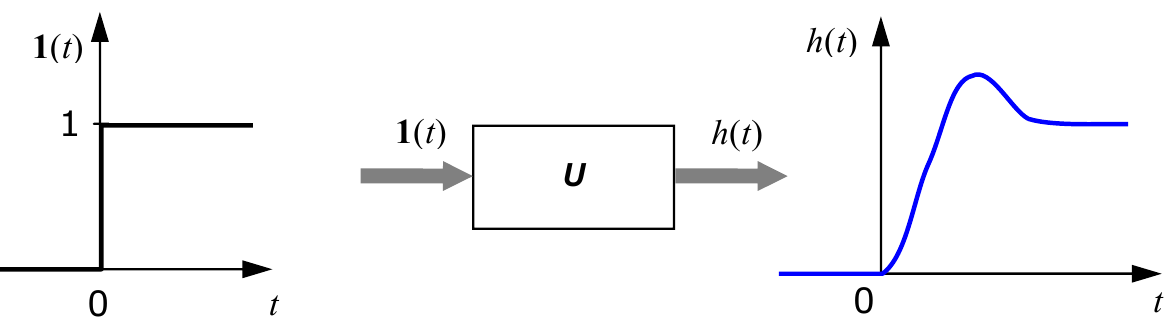
При этом предполагается, что объект в начальный момент находится в состоянии покоя, то есть, имеет нулевые начальные условия. Это значит, что все его переменные состояния равны нулю и внутренняя энергия также нулевая.
Если начальные условия ненулевые, то для построения сигнала выхода при любом входе нужно использовать дифференциальные уравнения объекта или модель в пространстве состояний. Это значит, что переходная характеристика дает меньше информации, чем исходные уравнения.
Пусть модель объекта задана дифференциальным уравнением первого порядка
$$T \frac{\mathrm{d}y(t)}{\mathrm{d}t}+y(t)=k·x(t),$$где $k$ – безразмерный коэффициент, а $T$ – некоторая постоянная, которая имеет размерность времени (измеряется в секундах). Найдем переходную характеристику этого звена. Решая уравнение при $x(t)=1(t)$, получаем
$$y(t)=k+C_1·exp\left(\frac{-t}{T}\right),$$где постоянная $C_1$ должна определяться из начальных условий. Поскольку нас интересует переходная характеристика, начальные условия считаем нулевыми, то есть $y(0)=0$, что дает $C_1=-k$ и поэтому
$$h(t)=y(t)=k·\left(1-exp\left(\frac{-t}{T}\right)\right),$$На рисунке показаны переходные характеристики модели при различных значениях параметра $T$, который называется постоянной времени звена.
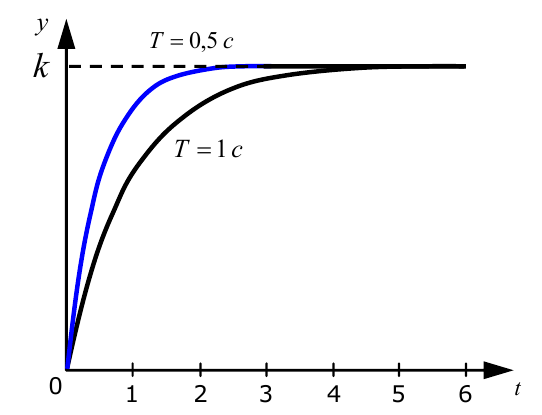
Видно, что при увеличении $T$ выход $y(t)$ медленнее достигает установившегося значения, равного $k$, то есть постоянная времени характеризует инерционность звена. Чем больше постоянная времени, чем медленнее реагирует объект на управление и тем больше усилий нужно для того, чтобы перевести его в новое состояние.
Заметим, что ступенчатый сигнал легко получить на практике, поэтому переходную характеристику можно снять экспериментально.
В качестве тестового сигнала можно, в принципе, использовать любой сигнал. Например, можно изучать реакцию системы на прямоугольный импульс. Вопрос в том, чтобы определить некоторый стандартный вид этого импульса. На рисунке показаны три импульса, имеющих одинаковые площади. Для простоты будем считать, что эта площадь равна единице.
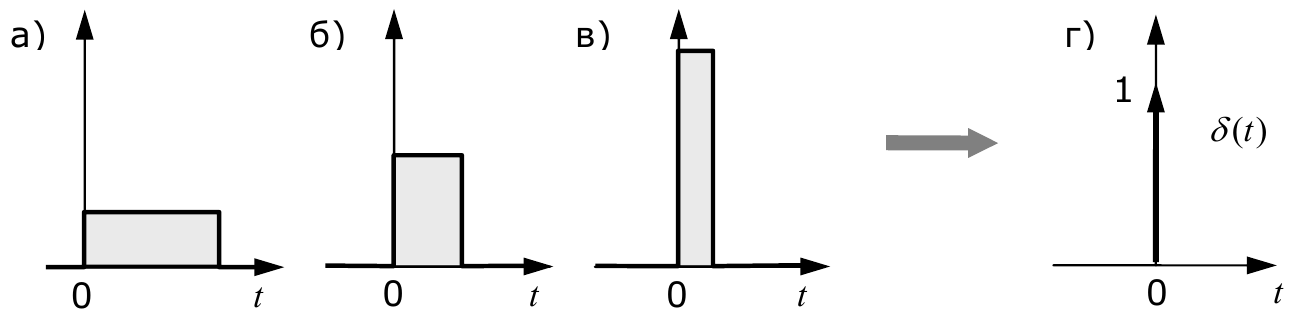
Что будет, если мы будем уменьшать ширину импульса, сохраняя его площадь? Очевидно, что высота импульса будет расти и в пределе (когда ширина стремится к нулю) станет бесконечной. Таким образом, мы получили еще один классический тестовый сигнал – единичный импульс или дельта-функцию Дирака $δ(t)$. Это идеальный (невозможный в реальной жизни) сигнал, который равен нулю во всех точках, кроме $t=0$, где он уходит к бесконечность, причем его площадь (интеграл по всей оси времени) равен единице:
$$δ(t)=\begin{cases} ∞,t = 0\\0, t ≠ 0\end{cases}.$$ $$∫_{-∞}^∞δ(t)\mathrm{d}t=1.$$Поскольку бесконечный импульс невозможно нарисовать, на графике он изображается стрелкой, высота которой равна единице.
Иногда определяют дельта-функцию как производную от единичного ступенчатого сигнала $1(t)$. Действительно, эта производная равна нулю при всех значениях $t$, кроме нуля, где она обращается в бесконечность.
Реакция системы на единичный импульс (дельта-функцию) называется импульсной характеристикой и обозначается $w(t)$:

Импульсная характеристика, так же, как и переходная характеристика, определяется при нулевых начальных условиях, то есть, объект должен находиться в состоянии покоя.
Рассматривая дельта-функцию как предельный случай прямоугольного сигнала единичной площади, можно найти связь между переходной функцией и импульсной характеристикой.
Пусть ширина прямоугольного импульса равна $ε$, а высота – $\frac{1}{ε}$ . Такой импульс можно представить в виде разности двух ступенчатых сигналов
$$x(t)=\frac{1}{ε}·(1(t)-1(t-ε)),$$где $1(t-ε)$ – это единичный ступенчатый сигнал, который приходит в момент $t=ε$, то есть, смещен по времени на $ε$.
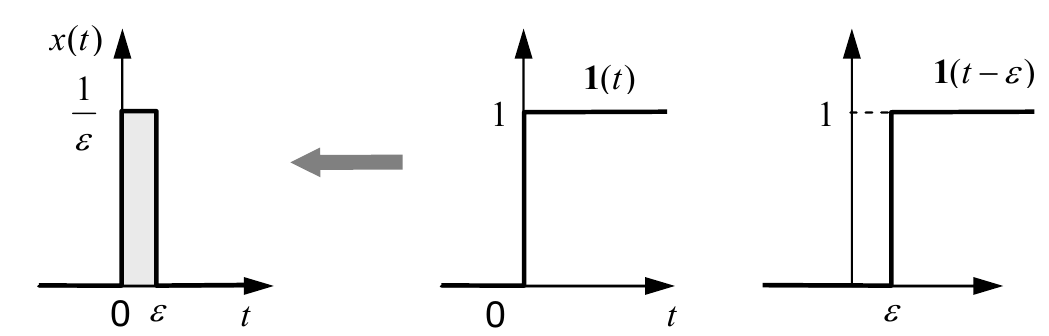
Так как для линейных систем справедлив принцип суперпозиции, сигнал на выходе будет равен разности реакций системы на входы $1(t)$ и $1(t–ε)$, умноженной на коэффициент $\frac{1}{ε}$. Учитывая, что реакция на сигнал $1(t)$ – это переходная функция $h(t)$, получаем
$$y(t)=\frac{1}{ε}·(h(t)-h(t-ε)).$$Переходя к пределу при $ε→0$, находим, что импульсная характеристика
$$w(t)= \lim_{ε\to 0}\frac{h(t)-h(t-ε)}{ε}=\frac{\mathrm{d}h(t)}{\mathrm{d}t},$$как оказывается, равна производной от переходной функции. Наоборот, переходная функция – это интеграл от импульсной характеристики на интервале от 0 до $t$:
$$h(t)=∫_0^t w(τ)\mathrm{d}τ.$$Дифференцируя переходную характеристику звена первого порядка, получаем соответствующую импульсную характеристику:
$$w(t)=\frac{\mathrm{d}}{\mathrm{d}t}\left(k·\left(1-exp\left(\frac{-t}{T}\right)\right)\right)=\frac{k}{T}·exp\left(\frac{-t}{T}\right).$$Другое название импульсной характеристики – весовая функция. Это название связано с тем, что для произвольного входного сигнала $x(t)$ выход системы $y(t)$ при нулевых начальных условиях вычисляется как интеграл
$$y(t)=∫_{-∞}^t x(τ)·w(t-τ)\mathrm{d}τ = ∫_0^∞ x(t-τ)·w(τ)\mathrm{d}τ.$$Здесь функция $w(t)$ как бы «взвешивает» входной сигнал $x(t)$ в подынтегральном выражении.
Заметим, что импульсная характеристика дает неполную информацию об объекте, поскольку не учитывает ненулевые начальные условия.
В отличие от ступенчатого сигнала, мгновенный импульс бесконечной величины невозможно получить на реальном устройстве, поэтому снять импульсную характеристику системы, строго говоря, экспериментально не удается.
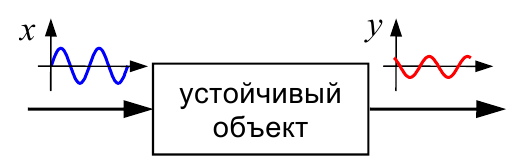
Еще один популярный эталонный сигнал – гармонический (синус, косинус), например:
$$x(t)=sin(ω·t),$$где $ω$ – угловая частота (в радианах в секунду). Можно показать, что при таком входе на выходе линейной системы в установившемся режиме (при больших $t$) будет синус той же частоты, но с другой амплитудой $A$ и сдвигом фазы $φ$:
$$y(t)=A(ω)·sin(ω·t+φ(ω)).$$Для каждой частоты входного сигнала будет своя амплитуда и свой сдвиг фазы. Чтобы определить по графику фазовый сдвиг $φ$, нужно найти расстояние $∆t$ по оси времени между соответствующими точками синусоид (например, точками пересечения с осью $t$ или вершинами). Если $∆t$ умножить на частоту $ω$, получаем сдвиг фазы $φ$ (в радианах).
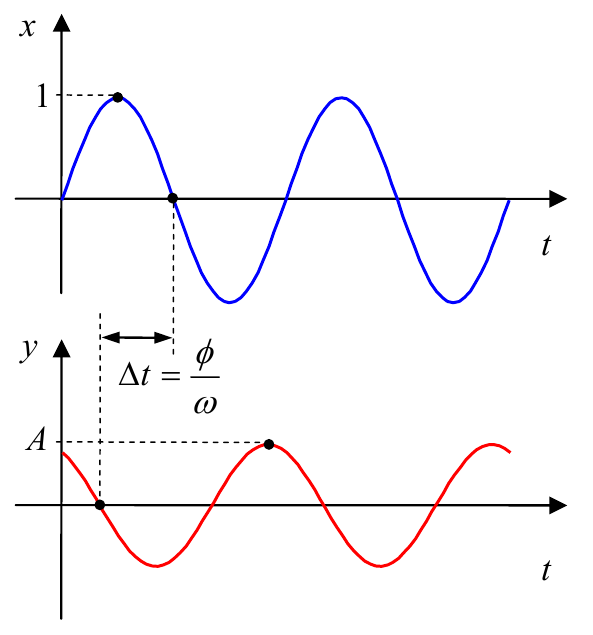
На рисунке показан случай $φ>0$ (опережение по фазе), когда выход сдвинут «влево» по оси времени относительно входа, то есть, «идет раньше» входного.
Зная передаточную функцию системы $W(s)$, можно вычислить амплитуду и сдвиг фазы по формулам
$$A(ω)=|W(jω)|,$$ $$φ(ω)=arg(W(jω))=arctg\left(\frac{Im(W(jω))}{Re(W(jω))} \right).$$Запись $W(jω)$ означает, что в передаточную функцию $W(s)$ подставляется чисто мнимое число $s=jω$, где $j=\sqrt{-1}$. Для каждой частоты ω значение $W(jω)=P+jQ$ – это некоторое комплексное число, имеющее амплитуду
$$|W(jω)|=\sqrt{P^2+Q^2}$$и фазу
$$arg(W(jω))=arctg\left(\frac{Q}{P}\right).$$Функция $W(jω)$ называется частотной характеристикой звена, поскольку она характеризует выход системы при гармонических сигналах разной частоты. Зависимости $P(ω)$ и $Q(ω)$ – это вещественная и мнимая частотные характеристики.
Функции $A(ω)$ и $φ(ω)$ называются соответственно амплитудной и фазовой частотными характеристиками (АЧХ и ФЧХ). Амплитудная частотная характеристика – это коэффициент усиления гармонического сигнала. Если на какой-то частоте ω значение $A(ω)>1$, входной сигнал усиливается, если $A(ω) < 1$, то вход данной частоты ослабляется.
По форме АЧХ различают несколько основных типов звеньев
На рисунке показаны амплитудные частотные характеристики идеальных фильтров этих четырех типов.
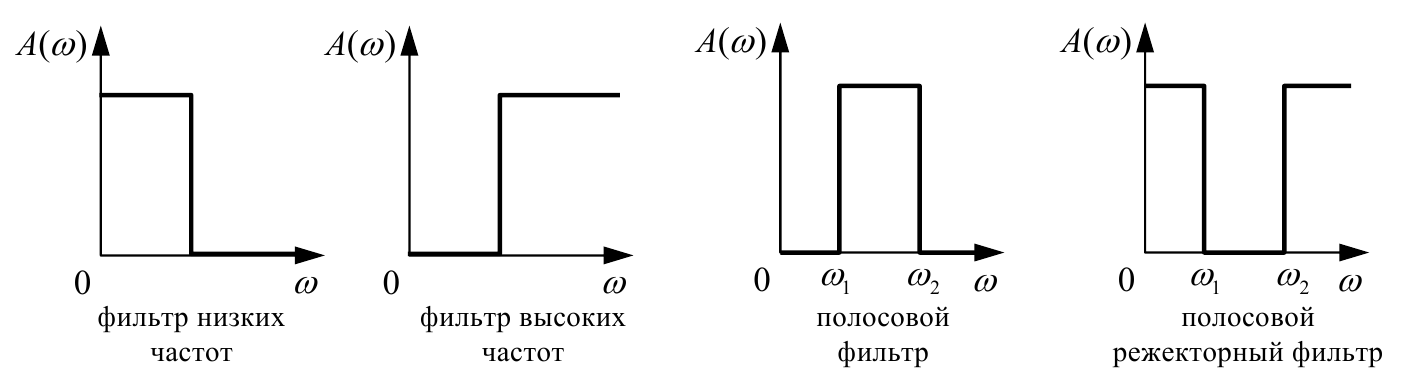
В радиотехнике используется понятие полосы пропускания – это ширина полосы частот, в которой значение АЧХ больше, чем $\frac{1}{\sqrt{2}}$ от ее максимального значения.
Частотные характеристики во многих случаях можно снять экспериментально. Если объект устойчивый, на его вход подается гармонический сигнал и записывается сигнал $y(t)$ на выходе. Определив амплитуду и сдвиг фазы для разных частот, можно построить по точкам амплитудную и фазовую частотные характеристики.