К основным термодинамическим процессам относят следующие четыре процесса:
В реальных условиях указанные ограничения практически не выполняются. В связи с этим в технической термодинамике существует понятие политропного процесса как общего случая термодинамического процесса. Предполагается, что политропный процесс обратим и теплоемкость рабочего тела (идеального газа) $с_n$ в ходе данного процесса не изменяется ($c_n=const$). Уравнение политропного процесса имеет вид:
$$pv^n=const,$$где $n=\frac{c_n-c_p}{c_n-c_v}$ – постоянная величина, называемая показателем политропы. Политропных процессов существует бесчисленное множество, т.к. $–∞ < c_n < ∞$ и $–∞ < n < ∞$.
Изохорный процесс – термодинамический процесс, который происходит при постоянном объёме. Параметры состояния идеального газа на изохоре связаны соотношением
$$\frac{p_2}{p_1} =\frac{T_2}{T_1}.$$В идеальном газе повышение температуры (нагрев газа) в сосуде постоянного объема всегда приводит к росту давления, причем давление растет тем быстрее, чем меньше значение v на данной изохоре.
Работа расширения системы в изохорном процессе равна нулю:
$$l=\intop_{v_1}^{v_2} p \mathrm{d}v=0.$$Количество теплоты, сообщаемой системе при нагреве в изохорном процессе, определяется из уравнения первого закона термодинамики:
$$\mathrm{d}q=\mathrm{d}u+\mathrm{d}l=\mathrm{d}u=c_v \mathrm{d}T,$$или
$$q=\intop_{T_1}^{T_2} c_v \mathrm{d}T.$$Изменение энтропии в изохорном процессе определяется следующим образом:
$$∆s=\intop_{T_1}^{T_2} \frac{c_v}{T} \mathrm{d}T+\intop_{v_1}^{v_2} \frac{R}{v} \mathrm{d}v=\intop_{T_1}^{T_2} \frac{c_v}{T} \mathrm{d}T.$$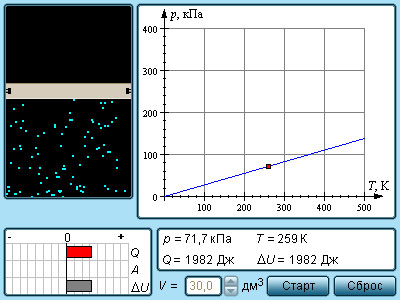
Изобарный процесс – термодинамический процесс, происходящий в системе при постоянном давлении. Параметры состояния идеального газа на изобаре связаны соотношением:
$$\frac{v_2}{v_1} =\frac{T_2}{T_1}.$$Отсюда следует, что чем выше температура газа, тем больше его удельный объем (т.е. тем меньше плотность). При этом величина v на изобаре при повышении температуры растет тем быстрее, чем меньше давление.
Работа расширения системы в изобарном процессе определяется следующим образом:
$$l=\intop_{v_1}^{v_2} p \mathrm{d}v=p·(v_2-v_1).$$Для идеального газа работа расширения системы в изобарном процессе может быть представлена также в следующем виде:
$$l=R·(T_2-T_1).$$Количество теплоты, сообщаемой системе при нагреве (или отдаваемой системой при охлаждении) в изобарном процессе, определяется следующим образом:
$$\mathrm{d}q=\mathrm{d}h+\mathrm{d}l'=\mathrm{d}h-v \mathrm{d}p=\mathrm{d}h=c_p \mathrm{d}T,$$или
$$q=\intop_{T_1}^{T_2} c_p \mathrm{d}T.$$Изменение энтропии в изобарном процессе, т.е. разность энтропий, соответствующих состояниям 1 и 2, определяется из соотношения:
$$∆s=\intop_{T_1}^{T_2} \frac{c_p}{T} \mathrm{d}T-\intop_{p_1}^{p_2} \frac{R}{p} \mathrm{d}p=\intop_{T_1}^{T_2} \frac{c_p}{T} \mathrm{d}T.$$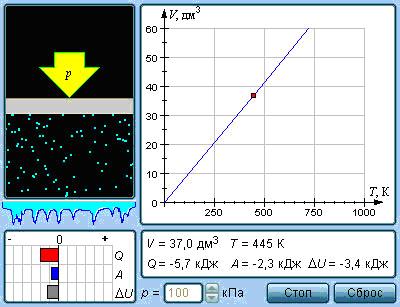
Изотермический процесс – процесс изменения состояния термодинамической системы при постоянной температуре.
Для идеального газа давления и объемы в любых точках на изотерме связаны уравнением Бойля—Мариотта, т.е. зависимость объема от давления на изотерме для идеального газа имеет характер гиперболы:
$$p·v=const,$$или
$$\frac{p_1}{p_2} =\frac{v_2}{v_1}.$$Работа расширения системы в изотермическом процессе между точками изотермы 1 и 2 определяется с помощью общего соотношения:
$$l=\intop_{v_1}^{v_2} p\mathrm{d}v=R·T·\intop_{v_1}^{v_2} \frac{\mathrm{d}v}{v}=p_1·v_1·\intop_{v_1}^{v_2} \frac{\mathrm{d}v}{v}.$$Количество теплоты , подводимой к системе (или отдаваемой системой) в изотермическом процессе, определяется из известного соотношения:
$$\mathrm{d}q=T \mathrm{d}s,$$или
$$q=\intop_{s_1}^{s_2} T \mathrm{d}s=T·(s_2-s_1).$$Количество работы, совершаемой идеальным газом в изотермическом процессе, равно количеству теплоты, подведенной к этому газу:
$$q=l.$$Изменение энтропии в изотермическом процессе, т.е. разность энтропий, соответствующих состояниям 1 и 2, вычисляется следующим способом:
$$∆s=\intop_{T_1}^{T_2} \frac{c_v}{T} \mathrm{d}T+\intop_{v_1}^{v_2} \frac{R}{v} \mathrm{d}v=\intop_{v_1}^{v_2} \frac{R}{v} \mathrm{d}v.$$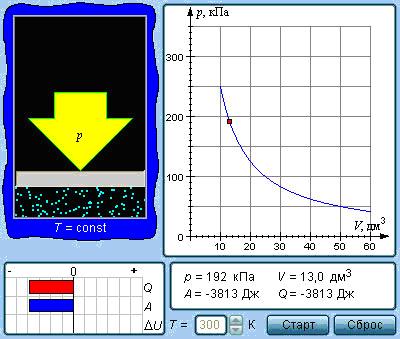
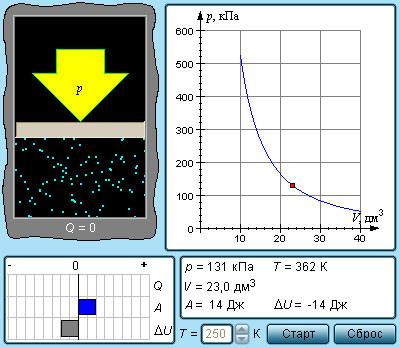
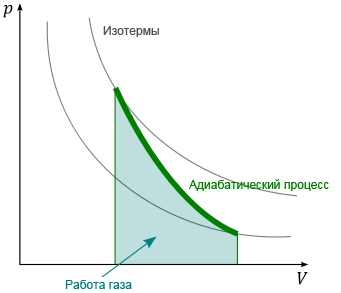
Адиабатный процесс – такой термодинамический процесс, в котором к системе не подводится и от системы не отводится теплота. Термодинамическую систему, в которой протекает адиабатный процесс, можно представить себе в виде некоторого объема, ограниченного оболочкой, снабженной идеальной теплоизоляцией, абсолютно не пропускающей теплоту. В реальных условиях процесс является адиабатным в тех случаях, когда система снабжена хорошей теплоизоляцией или когда процесс расширения (сжатия) газа происходит настолько быстро, что не успевает произойти скольконибудь заметный теплообмен газа с окружающей средой.
Поскольку для обратимого процесса $\mathrm{d}q=T \mathrm{d}s$, получаем, что в обратимом адиабатном процессе $\mathrm{d}s=0$, т.е. энтропия системы сохраняется постоянной. Иными словами, обратимый адиабатный процесс является в то же время изоэнтропным процессом.
Для любого состояния системы в изоэнтропном процессе справедливо соотношение Пуассона:
$$p·v^k=const.$$Если показатель изоэнтропы $k$ изменяется с изменением состояния системы и известен характер зависимости $k$ на изоэнтропе, то для расчета величины $p_2$ по известным $p_1$, $v_1$ и $v_2$ следует вычислить интеграл, стоящий в правой части по известным значениям $k$.
Для идеального газа показатель изоэнтропы $k$ можно определить:
$$k=\frac{c_p}{c_v}.$$Так как для идеального газа $c_p=c_v+µR$, тогда:
$$k=1+\frac{µR}{c_v}.$$Как известно, теплоемкости идеального газа слабо изменяются с температурой, поэтому и величину $k$ с высокой степенью точности можно считать практически не зависящей от температуры. Известно, что мольная изохорная теплоемкость $μс_v$ идеального газа равна примерно $13$ кДж/(кмоль·К) для одноатомного идеального газа, $21$ кДж/(кмоль·К) для двухатомного и $29$ кДж/(кмоль·К) для трех- и многоатомного газа. Поскольку $µR≈8.3$ кДж/(кмоль·К), то получаем следующие примерные значения показателя изоэнтропы $k$ идеального газа: одноатомный $k=1.67$, двухатомный $k=1.40$, трех- и многоатомный $k=1.29$. Для воздуха показатель изоэнтропы в идеально-газовом состоянии равен примерно $1.40$.
Для изоэнтропного процесса в идеальном газе можно получить соотношения, связывающие между собой значения $p$, $Т$ и $v$:
$$\frac{p_2}{p_1} =\left(\frac{v_1}{v_2}\right)^k,$$ $$\frac{T_2}{T_1} =\left(\frac{v_1}{v_2}\right)^{k-1},$$ $$\frac{T_2}{T_1} =\left(\frac{p_2}{p_1}\right)^{\frac{k-1}{k}}.$$Работа расширения системы в изоэнтропном процессе определяется следующим образом:
$$\mathrm{d}l=-\mathrm{d}u=-c_v \mathrm{d}T,$$или
$$l=-\intop_{T_1}^{T_2} c_v \mathrm{d}T.$$Таким образом, в адиабатном процессе работа расширения системы совершается за счет убыли внутренней энергии системы. Это и понятно – ведь в адиабатном процессе к системе нет притока теплоты извне и единственный источник энергии для совершения работы – внутренняя энергия самой системы.
В случае идеального газа уравнения для расчета работы расширения могут быть представлены также в иной форме:
$$l=\intop_{v_1}^{v_2} p \mathrm{d}v=\intop_{v_1}^{v_2} \frac{p_1·v_1^k}{v^k} \mathrm{d}v=\frac{p_1·v_1}{k-1}·\left(1-\left(\frac{v_1}{v_2}\right)^{k-1}\right).$$Следует подчеркнуть, что уравнение выше пригодно для расчета в том случае, если в интервале параметров между точками 1 и 2 показатель изоэнтропы $k$ сохраняется постоянным.
Политропные процессы. Политропными называют термодинамические процессы, удовлетворяющие уравнению:
$$p·v^n=const.$$при произвольном, постоянном для данного процесса значении $n$.
Понятие о политропных процессах было введено в термодинамике по аналогии с понятием об адиабатных процессах. Уравнение политропного процесса по внешнему виду сходно с уравнением адиабаты, однако существенная разница между этими уравнениями состоит в том, что если показатель изоэнтропы (адиабаты) $k$ является в общем случае величиной переменной, то уже само понятие политропного процесса основано на предположении о том, что показатель политропы n является постоянной величиной. В политропном процессе к системе может подводиться (или отводиться от нее) теплота.
Понятие о политропных процессах широко используется главным образом при изучении процессов сжатия и расширения в газовых двигателях, зачастую политропные процессы оказываются удобными для аппроксимации действительных газовых процессов в двигателях. Реальные процессы сжатия в газовых двигателях и компрессорах часто не являются ни адиабатными, ни изотермическими, а занимают промежуточное положение между этими двумя видами процессов. Поэтому обычно встречаемые на практике значения показателя n политропного процесса лежат в интервале от $1$ до $k$.
Если политропный процесс осуществляется в идеальном газе, то нетрудно получить зависимости между начальными и конечными параметрами процесса:
$$\frac{p_2}{p_1} =\left(\frac{v_1}{v_2}\right)^n,$$ $$\frac{T_2}{T_1} =\left(\frac{v_1}{v_2}\right)^{n-1},$$ $$\frac{T_2}{T_1} =\left(\frac{p_2}{p_1}\right)^{\frac{n-1}{n}}.$$Работа расширения системы в политропном процессе между точками 1 и 2 определяется с помощью уравнения:
$$l=\intop_{v_1}^{v_2} p\mathrm{d}v=\intop_{v_1}^{v_2} \frac{p_1·v_1^n}{v^n} \mathrm{d}v=\frac{p_1·v_1}{n-1}·\left(1-\left(\frac{v_1}{v_2}\right)^{n-1}\right).$$Это уравнение можно преобразовать в вид:
$$l=\frac{p_1·v_1}{n-1}·\left(1-\left(\frac{p_2}{p_1}\right)^{\frac{n-1}{n}}\right)=\frac{R·T_1}{n-1}·\left(1-\left(\frac{v_1}{v_2}\right)^{n-1}\right)=\frac{R·T_1}{n-1}·\left(1-\left(\frac{p_2}{p_1}\right)^{\frac{n-1}{n}}\right).$$или
$$l=\frac{p_1·v_1}{n-1}·\left(1-\frac{T_2}{T_1}\right)=\frac{R}{n-1}·(T_1-T_2)=\frac{p_1·v_1-p_2·v_2}{n-1}.$$Количество теплоты , подводимой к системе (или отводимой от нее) в политропном процессе можно определить с помощью уравнения первого закона термодинамики:
$$\mathrm{d}q=\mathrm{d}u+\mathrm{d}l=c_v \mathrm{d}T+p\mathrm{d}v,$$или
$$q=c_v·(T_2-T_1)+\frac{R}{n-1}·(T_1-T_2)= c_v·\frac{k-n}{n-1}·(T_2-T_1).$$Тогда теплоемкость идеального газа в политропном процессе:
$$c_n= c_v·\frac{k-n}{n-1}.$$Изменение энтропии системы в политропном процессе, т.е. разность энтропий, соответствующих точкам 1 и 2 на политропе, определяется из соотношения:
$$∆s=\intop_{T_1}^{T_2} \frac{c_n}{T} \mathrm{d}T=c_n·\ln\left(\frac{T_2}{T_1}\right).$$Для того чтобы определить значение показателя политропы для того или иного конкретного газового процесса, надо располагать экспериментальными данными для этого процесса.