Чаще всего регулятор включается перед объектом, как показано на схеме:
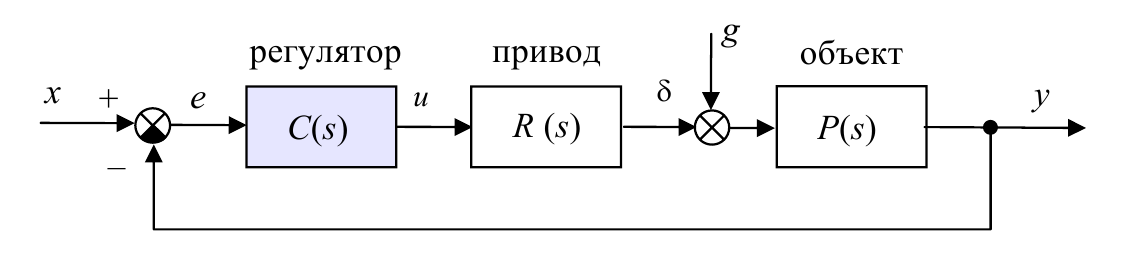
Задача системы управления состоит в том, чтобы подавить действие внешнего возмущения $g(t)$ и обеспечить быстрые и качественные переходные процессы. К сожалению, эти задачи часто противоречивы. Фактически нам нужно скорректировать систему так, чтобы она имела нужные передаточные функции по возмущению $W_g (s)$, от входа $g(t)$ к выходу $y(t)$, и по задающему воздействию $W(s)$, от входа $x(t)$ к выходу $y(t)$
$$W_g (s)=\frac{P(s)}{1+C(s)R(s)P(s)},$$ $$W(s)=\frac{C(s)R(s)P(s)}{1+C(s)R(s)P(s)}.$$Для этого мы можем использовать только один регулятор $C(s)$, поэтому такую систему называют системой с одной степенью свободы.
Легко проверить, что эти две передаточные функции связаны равенством
$$W_g (s)=(1-W(s))·P(s).$$Поэтому, изменяя одну из передаточных функций, мы автоматически меняем и вторую. Таким образом, их невозможно сформировать независимо и решение всегда будет некоторым компромиссом.
Посмотрим, можно ли в такой системе обеспечить нулевую ошибку, то есть, абсолютно точное отслеживание входного сигнала. Передаточная функция по ошибке (от входа $x(t)$ к ошибке $e(t)$) равна
$$W_e (s)=\frac{1}{1+C(s)R(s)P(s)}.$$Для того, чтобы ошибка всегда была нулевой, требуется, чтобы эта передаточная функция была равна нулю. Поскольку ее числитель – не нуль, сразу получаем, что знаменатель должен обращаться в бесконечность. Мы может влиять только на регулятор $C(s)$ (остальные элементы заданы заранее), поэтому получаем $C(s)→∞$. Таким образом, для уменьшения ошибки нужно увеличивать коэффициент усиления регулятора. Это так называемый принцип глубокой обратной связи.
Однако нельзя увеличивать усиление до бесконечности. Во-первых, все реальные устройства имеют предельно допустимые значения входных и выходных сигналов. Во-вторых, при большом усилении контура ухудшается качество переходных процессов, усиливается влияние возмущений и шумов, система может потерять устойчивость. Поэтому в схеме с одной степенью свободы обеспечить нулевую ошибку слежения невозможно.