Такой регулятор называется пропорционально-интегральным или ПИ-регулятором. Интегратор выдает сигнал, пропорциональный накопленной ошибке, поэтому переходный процесс несколько замедляется. Однако за счет интегрального канала обеспечивается нулевая ошибка в установившемся состоянии при ступенчатом возмущении и ступенчатом изменении задающего сигнала-уставки.
На рисунке ниже показаны переходные характеристики замкнутой системы с И-регулятором и объектом второго порядка вида
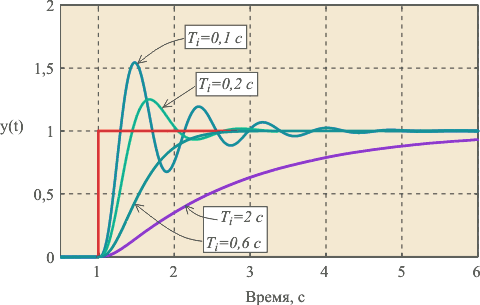
При больших постоянных интегрирования переходная характеристика имеет вид, сходный с характеристикой апериодического звена. С уменьшением постоянных интегрирования растет усиление регулятора и когда петлевое усиление контура с обратной связью приближается к 1, в системе появляются колебания.
ПИ-регулятор имеет два существенных положительных отличия от И-регулятора: во-первых, его усиление на всех частотах не может стать меньше $K$, следовательно, увеличивается динамическая точность регулирования, во-вторых, по сравнению с И-регулятором, он вносит дополнительный сдвиг фаз только в области низких частот, что увеличивает запас устойчивости замкнутой системы. Оба фактора дают дополнительные степени свободы для оптимизации качества регулирования. В то же время, как и в И-регуляторе, модуль коэффициента передачи регулятора с уменьшением частоты стремится к бесконечности, обеспечивая тем самым нулевую ошибку в установившемся режиме. Отсутствие сдвига фаз на высоких частотах позволяет увеличить скорость нарастания управляемой переменной (по сравнению с И-регулятором) без снижения запаса устойчивости. Однако это справедливо до тех пор, пока пропорциональный коэффициент не станет настолько большой, что увеличит усиление контура до единицы.
Переходный процесс в ПИ-регуляторе показан на рисунке ниже.
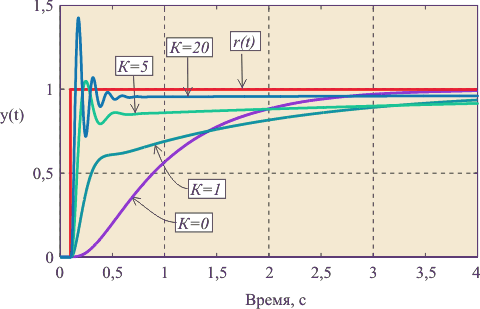
С ростом пропорционального коэффициента появляется дополнительная ошибка во время переходного процесса, которая уменьшается с ростом $K$, однако при этом снижается запас устойчивости системы, поскольку с ростом $K$ увеличивается усиление на частоте . Это приводит к появлению затухающих колебаний в начале переходного процесса. Когда величина становится достаточно большой для компенсации ослабления сигнала в объекте, в системе появляются незатухающие колебания.
Следует отметить, что в отличие от П-регулятора, в котором ошибка остается в установившемся режиме, наличие интегрального члена в ПИ-регуляторе сводит эту ошибку в идеальном регуляторе до нуля, как в И-регуляторе.
Однако появление пропорционального коэффициента приводит к затягиванию переходного процесса по сравнению с И-регулятором. Объясняется это тем, что в ПИ-регуляторе сигнал ошибки, поступающий на вход интегратора, меньше, чем в И-регуляторе (он уменьшается благодаря пропорциональному коэффициенту), поэтому сигнал, компенсирующий ошибку нарастает медленнее, чем в И-регуляторе.
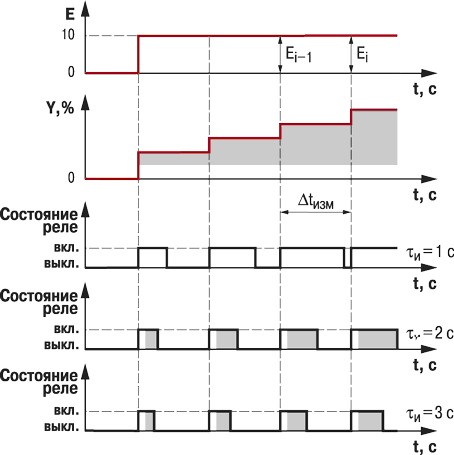
При работе прибора в режиме ПИ-регулятора величина выходного сигнала $Y_i$ зависит как от величины отклонения $E_i$, так и от суммы предыдущих рассогласований:
$$Y_i=\frac{1}{X_p}·\left(E_i+\frac{1}{τ_и}·\sum_{i=0}^n E_i·∆t_{изм}\right)·100%.$$где $X_p$ – полоса пропорциональности; $E_i$ – рассогласование; $τ_и$ – постоянная времени интегрирования; $\sum_{i=0}^n E_i·∆t_{изм}$ – накопленная в i-й момент времени сумма рассогласований (интегральная сумма).
Из рисунка видно, что в первый момент времени, когда нет отклонения ($E_i=0$), нет и выходного сигнала ($Y_i=0$). С появлением отклонения $E_i$ появляются импульсы, длительность которых постепенно увеличивается. В импульсах присутствует пропорциональная составляющая, которая зависит от величины $E$ (незаштрихованная часть импульсов) и интегральная составляющая (заштрихованная часть). Увеличение длительности импульсов происходит за счет роста интегральной составляющей, которая зависит от рассогласования $E_i$ и коэффициента $τ_и$.