Несмотря на развитые современные методы проектирования сложных регуляторов, подавляющее большинство промышленных систем управления основаны на регуляторах первого и второго порядка. Эти регуляторы во многих случаях могут обеспечить приемлемое управление, легко настраиваются и дешевы при массовом изготовлении.
Простейший регулятор – пропорциональный или П-регулятор – это простой усилитель с передаточной функцией $C(s)=K$. Его выход – это ошибка управления $e(t)$, умноженная на коэффициент $K$. С помощью П-регулятора можно управлять любым устойчивым объектом, однако он дает относительно медленные переходные процессы и ненулевую статическую ошибку.
Чтобы убрать статическую ошибку в установившемся режиме, в регулятор вводят интегральный канал с коэффициентом усиления $K_I$, так что
$$C(s)=K+\frac{K_I}{s},$$ $$u(t)=Ke(t)+K_I ∫_0^t e(t)\mathrm{d}t.$$Такой регулятор называется пропорционально-интегральным или ПИ-регулятором. Интегратор выдает сигнал, пропорциональный накопленной ошибке, поэтому переходный процесс несколько замедляется. Однако за счет интегрального канала обеспечивается нулевая ошибка в установившемся состоянии при ступенчатом возмущении и ступенчатом изменении задающего сигнала-уставки.
Для ускорения переходных процессов добавляют дифференциальный канал с коэффициентом усиления $K_D$:
$$C(s)=K+\frac{K_I}{s}+K_D s,$$ $$u(t)=Ke(t)+K_I ∫_0^t e(t)\mathrm{d}t+K_D \frac{\mathrm{d}e(t)}{\mathrm{d}t}.$$Такой регулятор называется ПИД-регулятором (пропорционально-интегрально-дифференциальный). Регуляторы этого типа очень хорошо зарекомендовали себя в практических задачах.
Управление по производной – это быстрый способ управления. Сигнал дифференциального канала наиболее важен при изменениях входов и исчезает в установившемся режиме. Он позволяет реагировать не на само увеличение ошибки, а на тенденцию ее изменения, и принять «превентивные меры». Главный недостаток дифференциального канала – большое влияние высокочастотных помех, например, шумов измерений. Для того, чтобы сделать регулятор физически реализуемым, вместо чистого дифференцирования используют инерционное дифференцирующее звено:
$$C(s)=K+\frac{K_I}{s}+\frac{K_D s}{T_D s+1},$$где $T_D$ – малая постоянная времени. Чем меньше $T_D$, тем в большем частотном диапазоне выполняется точное дифференцирование, но сильнее влияют высокочастотные помехи.
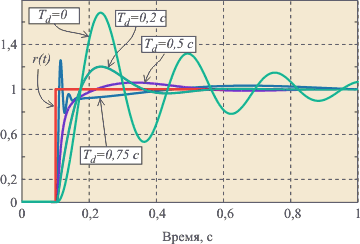
Для устойчивого объекта можно выбрать коэффициенты регулятора опытным путем, выполняя эксперименты с реальным объектом. Предложено несколько методов решения этой задачи, например, правила Зиглера-Никольса или Коэна-Куна.
Программная реализация ПИД-регулятора вырабатывает выходной сигнал, который рассчитывается по следующей формуле:
$$Y_i=\frac{1}{X_p}·\left(E_i+T_D·\frac{∆E_i}{∆t_{изм}} + \frac{1}{T_I} \sum_{i=0}^n E_i·∆t_{изм} \right)·100%.$$где $X_p$ – полоса пропорциональности, $E_i$ – рассогласование, $∆E_i$ – разность между двумя соседними измерениями $E_i$ и $E_{i-1}$, {∆t_{изм}} – время между двумя соседними измерениями $T_i$ и $T_{i-1}$ – постоянная времени интегрирования, $\sum_{i=0}^n E_i·∆t_{изм}$ – накопленная в i-й момент времени сумма рассогласований (интегральная сумма).
Сигнал управления является суммой трех составляющих: