Под криптографической защитой информации понимается такое преобразование исходной информации, в результате которого она становится недоступной для ознакомления и использования лицами, не имеющими на это полномочий. Известны различные подходы к классификации методов криптографического преобразования информации. По виду воздействия на исходную информацию методы криптографического преобразования информации могут быть разделены на четыре группы.
Шифрование информации. Основным видом криптографического преобразования информации в компьютерных системах является шифрование. Под шифрованием понимается процесс преобразования открытой информации в зашифрованную (шифротекст) или процесс обратного преобразования зашифрованной информации в открытую. Процесс преобразования открытой информации в закрытую получил название шифрование, а процесс преобразования закрытой информации в открытую – расшифрование. Процесс шифрования заключается в проведении обратимых математических, логических, комбинаторных и других преобразований исходной информации, в результате которых зашифрованная информация представляет собой хаотический набор букв, цифр, других символов и двоичных кодов. Для шифрования информации используются алгоритм преобразования и ключ. Как правило, алгоритм для определенного метода шифрования является неизменным. Исходными данными для алгоритма шифрования служат информация, подлежащая шифрованию, и ключ шифрования. Ключ – конкретное значение некоторых параметров алгоритма криптографического преобразования, обеспечивающее выбор преобразования из семейства. Он содержит управляющую информацию, которая определяет выбор преобразования на определенных шагах алгоритма и величины операндов, используемые при реализации алгоритма шифрования.
Стеганография. В отличие от других методов криптографического преобразования информации, методы стеганографии позволяют скрыть не только смысл хранящейся или передаваемой информации, но и сам факт хранения или передачи закрытой информации. В компьютерных системах практическое использование стеганографии только начинается, но проведенные исследования показывают ее перспективность. В основе всех методов стеганографии лежит маскирование закрытой информации среди открытых файлов. Обработка мультимедийных файлов в компьютерных системах открыла практически неограниченные возможности перед стеганографией.
Существует несколько методов скрытой передачи информации. Одним из них является простой метод скрытия файлов при работе в операционной системе Windows. За текстовым открытым файлом записывается скрытый двоичный файл, объем которого много меньше текстового файла. В конце текстового файла помещается метка EOF (комбинация клавиш Ctrl и Z). При обращении к этому текстовому файлу стандартными средствами ОС считывание прекращается по достижению метки EOF, и скрытый файл остается недоступен. Для двоичных файлов никаких меток в конце файла не предусмотрено. Конец такого файла определяется при обработке атрибутов, в которых хранится длина файла в байтах. Доступ к скрытому файлу может быть получен, если файл открыть как двоичный. Скрытый файл может быть зашифрован. Если кто-то случайно обнаружит скрытый файл, то зашифрованная информация будет воспринята как сбой в работе системы.
Другой метод заключается в использовании графической и звуковой информации. Так, в графических объектах наименьший элемент изображения может кодироваться одним байтом. В младшие разряды определенных байтов изображения в соответствии с алгоритмом криптографического преобразования помещаются биты скрытого файла. Если правильно подобрать алгоритм преобразования и изображение, на фоне которого помещается скрытый файл, то человеческому глазу практически невозможно отличить полученное изображение от исходного. Очень сложно выявить скрытую информацию и с помощью специальных программ. Наилучшим образом для внедрения скрытой информации подходят изображения местности: фотоснимки со спутников, самолетов и т.п. С помощью средств стеганографии могут маскироваться текст, изображение, речь, цифровая подпись, зашифрованное сообщение. Комплексное использование стеганографии и шифрования многократно повышает сложность решения задачи обнаружения и раскрытия конфиденциальной информации.
Кодирование информации. Содержанием процесса кодирования информации является замена смысловых конструкций исходной информации (слов, предложений) кодами. В качестве кодов могут использоваться сочетания букв, цифр, букв и цифр. При кодировании и обратном преобразовании используются специальные таблицы или словари. Кодирование информации целесообразно применять в системах с ограниченным набором смысловых конструкций. Такой вид криптографического преобразования применим, например, в командных линиях автоматизированных систем управления.
Сжатие информации может быть отнесено к методам криптографического преобразования информации с определенными оговорками. Целью сжатия является сокращение объема информации. В то же время сжатая информация не может быть прочитана или использована без обратного преобразования. Учитывая доступность средств сжатия и обратного преобразования, эти методы нельзя рассматривать как надежные средства криптографического преобразования информации. Даже если держать в секрете алгоритмы, то они могут быть сравнительно легко раскрыты статистическими методами обработки. Поэтому сжатые файлы конфиденциальной информации подвергаются последующему шифрованию. Для сокращения времени целесообразно совмещать процесс сжатия и шифрования информации.
В некоторых источниках стеганография, кодирование и сжатие информации относятся к отраслям знаний, смежных с криптографией, но не входящих в нее.
К традиционным (классическим) методам шифрования относятся шифры перестановки, шифры простой и сложной замены, а также некоторые их модификации и комбинации. Комбинации шифров перестановок и шифров замены образуют все многообразие применяемых на практике симметричных шифров.
Шифры перестановки. При шифровании перестановкой символы шифруемого текста переставляются по определенному правилу в пределах блока этого текста. Шифры перестановки являются самыми простыми и, вероятно, самыми древними шифрами. Примером служат шифрующие таблицы. В качестве ключа в шифрующих таблицах используются: размер таблицы, слово или фраза, задающие перестановку, особенности структуры таблицы.
Шифры простой замены. При шифровании заменой (подстановкой) символы шифруемого текста заменяются символами того же или другого алфавита с заранее установленным правилом замены. В шифре простой замены каждый символ исходного текста заменяется символами того же алфавита по одному правилу на всем протяжении текста. Часто шифры простой замены называют шифрами одноалфавитной подстановки. Примером такой системы является система шифрования Цезаря. Шифр Цезаря является частным случаем шифра простой замены (одноалфавитной подстановки). Свое название этот шифр получил по имени римского императора Гая Юлия Цезаря, который использовал этот шифр при переписке. При шифровании исходного текста каждая буква заменялась на другую букву того же алфавита по следующему правилу. Заменяющая буква определялась путем смещения по алфавиту m от исходной буквы на k букв. При достижении конца алфавита выполнялся циклический переход к его началу. Цезарь использовал латинский алфавит $m = 26$ и шифр замены при смещении $k = 3$. Такой шифр замены можно задать таблицей подстановок, содержащей соответствующие пары букв открытого текста и шифротекста.
Пример простой реализации шифра Цезаря ня языке C#
using System;
namespace ConsoleApp
{
class Program
{
static void Main(string[] args)
{
string original = "Here is some data to encrypt!";
Console.WriteLine("Original: {0}", original);
byte[] b_original = System.Text.Encoding.ASCII.GetBytes(original); ;
byte k = 3;
for (int i = 0; i < b_original.Length; i++)
{
b_original[i] += k;
}
Console.WriteLine("Encrypted: {0}", System.Text.Encoding.ASCII.GetString(b_original, 0, b_original.Length));
Console.WriteLine(BitConverter.ToString(b_original));
for (int i = 0; i < b_original.Length; i++)
{
b_original[i] -= k;
}
Console.WriteLine("Round Trip: {0}", System.Text.Encoding.ASCII.GetString(b_original, 0, b_original.Length));
}
}
}
Шифрование методом гаммирования. Под гаммированием понимают процесс наложения по определенному закону гаммы шифра на открытые данные. Гамма шифра – это псевдослучайная последовательность, выработанная по заданному алгоритму для шифрования открытых данных и расшифрования принятых данных. Процесс шифрования заключается в генерации гаммы шифра и наложении полученной гаммы на исходный открытый текст обратимым образом, например, с использованием операции сложения по модулю 2. Перед шифрованием открытые данные разбивают на блоки одинаковой длины, обычно по 64 бита. Гамма шифра вырабатывается в виде последовательности аналогичной длины. Процесс расшифрования сводится к повторной генерации гаммы шифра и наложению этой гаммы на принятые данные. Получаемый этим методом шифротекст достаточно труден для раскрытия, поскольку теперь ключ является переменным. По сути дела, гамма шифра должна изменяться случайным образом для каждого шифруемого блока. Если период гаммы превышает длину всего шифруемого текста и злоумышленнику неизвестна никакая часть исходного текста, то такой шифр можно раскрыть только прямым перебором всех вариантов ключа. В этом случае криптостойкость шифра определяется длиной ключа.
В настоящее время наибольшее распространение получили системы использующие симметричное и ассиметричное шифрование.
Для работы применяется всего один пароль. Происходит всё следующим образом:
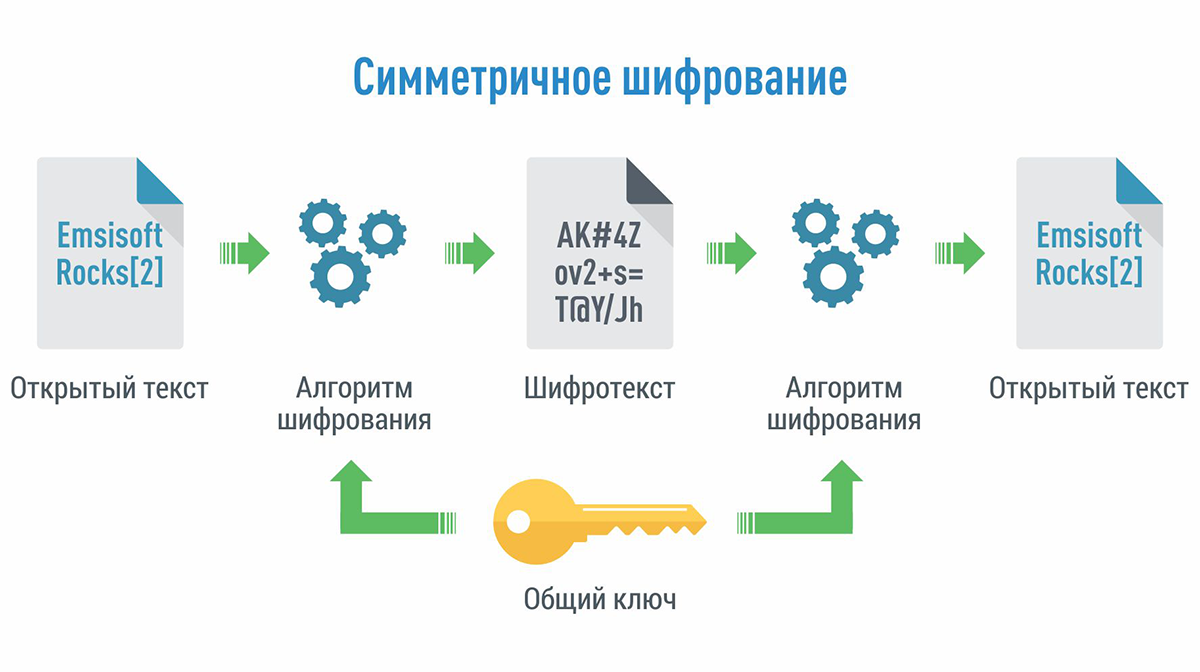
Используя подходы симметричного шифрования, необходимо особое внимание уделять вопросам создания и сохранения конфиденциальности пароля. Он должен быть сложным, что исключит подбор программным перебором значений. И не должен передаваться кому-нибудь в открытом виде как в сети, так и на физических носителях информации. Несмотря на свои ограничения и угрозу безопасности, подход до сих пор широко распространён в криптографии. Дело в том, что он очень прост в работе и понимании, а также работает очень быстро.
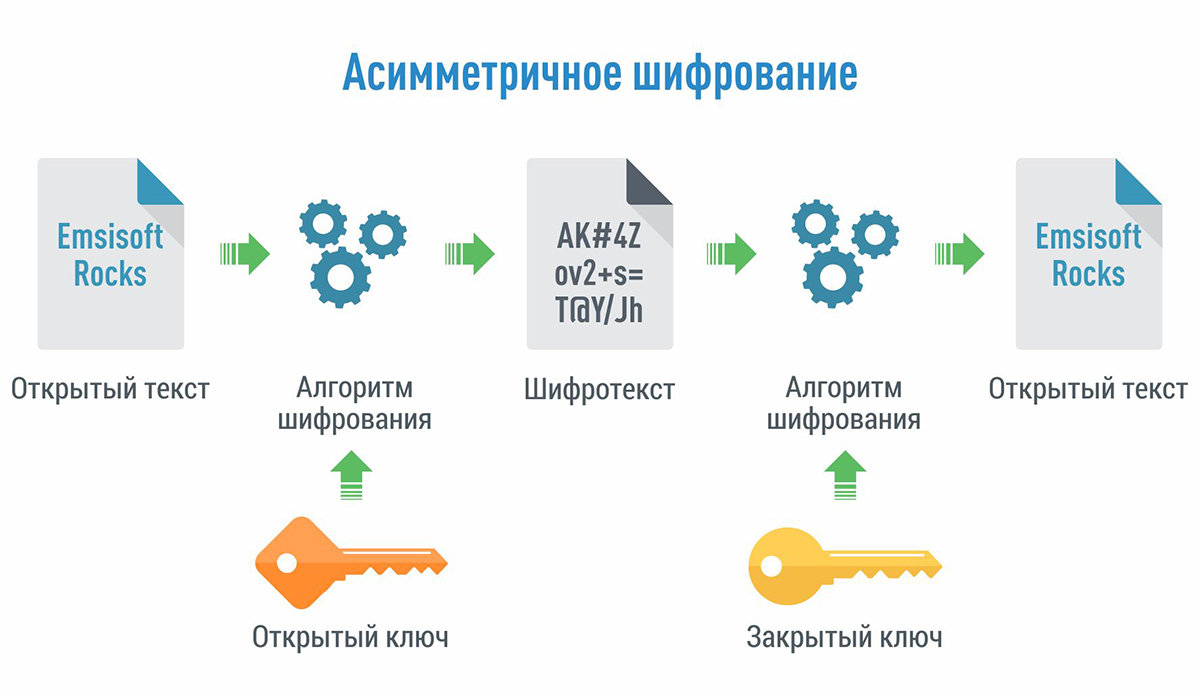
Для ассиметричного шифрования хранение паролей проще, ведь секретный ключ не нужно передавать кому-либо. А в случае взлома сервер сменит пару ключей и разошлёт всем новые комбинации. Считается, что ассиметричное шифрование «тяжелее» симметричного. Всё потому, что оно требует больше компьютерных ресурсов. Есть ограничения и на процесс генерации ключей. Как правило, возможности ассиметричного шифрования используют для выполнения идентификации пользователей (например, при входе на сайт). Или с его помощью создают сессионный ключ для симметричного шифрования (речь идёт о временном пароле для обмена данными между сервером и пользователем). Или формируют зашифрованные цифровые подписи. В последнем случае проверить такую подпись может каждый, используя публичный ключ, находящийся в открытом доступе.
AES, что означает Advanced Encryption Standard , является популярной формой шифрования, которая используется уже довольно долгое время для обеспечения надежного и безопасного хранения данных. AES-это симметричный тип шифрования, поскольку он использует один и тот же ключ для шифрования и дешифрования данных. Этот стандарт шифрования использует сетевой алгоритм перестановки подстановок (алгоритм SPN), чтобы применить несколько раундов шифрования для защиты данных. Тот факт, что он использует так много раундов, делает AES практически непроницаемым. AES - не только первый, но и единственный общедоступный шифр, одобренный NSA (Агентством национальной безопасности) для защиты сверхсекретных данных. Первоначально этот стандарт шифрования назывался Rijndael по именам двух его разработчиков, Винсента Реймена и Джоан Дэемен (оба из Бельгии).
AES включает три блочных шифра, и каждый из этих блочных шифров имеет разное количество возможных комбинаций клавиш, а именно:
Хотя существует три блочных шифра, каждый из них шифрует и дешифрует данные в 128 блочных битах с использованием ключей разной длины (т.е. 128, 192 и 256, как указано выше). Таким образом, можно с уверенностью сказать, что, хотя длина ключей может быть разной, размер блока всегда одинаков (128 бит или 16 байт).
Несмотря на то, что 256-битный ключ AES является просто самым сильным ключом в группе, часто называемый «военным», он не всегда используется по умолчанию, и причина почему это происходит из-за доступных или, что еще лучше, недоступных ресурсов. Чем больше размер ключа, тем больше ресурсов он потребляет, поэтому можно с уверенностью сказать, что менее способная система с большей вероятностью будет использовать 128-битные ключи AES вместо своих 256-битный аналог. Например, если вы используете на телефоне 256-битное шифрование AES, это может разрядить вашу батарею быстрее, чем 128-битная версия того же стандарта шифрования. 256-битные ключи AES намного сложнее подобрать, чем 128-битные. Однако даже при огромной вычислительной мощности 128-битные ключи AES по-прежнему практически невозможно взломать, поэтому использование этой версии вместо 256-битных ключей может быть лучшим выбором, если вас беспокоит мощность или задержка, особенно на портативных устройствах.
Распространенное использование AES:
Пример простой реализации шифра AES ня языке C#
using System;
using System.IO;
using System.Security.Cryptography;
namespace Aes_Example
{
class AesExample
{
public static void Main()
{
string original = "Here is some data to encrypt!";
// Create a new instance of the Aes
// class. This generates a new key and initialization
// vector (IV).
using (Aes myAes = Aes.Create())
{
// Encrypt the string to an array of bytes.
byte[] encrypted = EncryptStringToBytes_Aes(original, myAes.Key, myAes.IV);
// Decrypt the bytes to a string.
string roundtrip = DecryptStringFromBytes_Aes(encrypted, myAes.Key, myAes.IV);
//Display the original data and the decrypted data.
Console.WriteLine("Original: {0}", original);
Console.WriteLine("Encrypted: {0}", System.Text.Encoding.ASCII.GetString(encrypted,0,encrypted.Length));
Console.WriteLine("Encrypted bits: {0}", BitConverter.ToString( encrypted ) );
Console.WriteLine("Aes Key: {0}", BitConverter.ToString( myAes.Key ) );
Console.WriteLine("Round Trip: {0}", roundtrip);
}
}
static byte[] EncryptStringToBytes_Aes(string plainText, byte[] Key, byte[] IV)
{
// Check arguments.
if (plainText == null || plainText.Length <= 0)
throw new ArgumentNullException("plainText");
if (Key == null || Key.Length <= 0)
throw new ArgumentNullException("Key");
if (IV == null || IV.Length <= 0)
throw new ArgumentNullException("IV");
byte[] encrypted;
// Create an Aes object
// with the specified key and IV.
using (Aes aesAlg = Aes.Create())
{
aesAlg.Key = Key;
aesAlg.IV = IV;
// Create an encryptor to perform the stream transform.
ICryptoTransform encryptor = aesAlg.CreateEncryptor(aesAlg.Key, aesAlg.IV);
// Create the streams used for encryption.
using (MemoryStream msEncrypt = new MemoryStream())
{
using (CryptoStream csEncrypt = new CryptoStream(msEncrypt, encryptor, CryptoStreamMode.Write))
{
using (StreamWriter swEncrypt = new StreamWriter(csEncrypt))
{
//Write all data to the stream.
swEncrypt.Write(plainText);
}
encrypted = msEncrypt.ToArray();
}
}
}
// Return the encrypted bytes from the memory stream.
return encrypted;
}
static string DecryptStringFromBytes_Aes(byte[] cipherText, byte[] Key, byte[] IV)
{
// Check arguments.
if (cipherText == null || cipherText.Length <= 0)
throw new ArgumentNullException("cipherText");
if (Key == null || Key.Length <= 0)
throw new ArgumentNullException("Key");
if (IV == null || IV.Length <= 0)
throw new ArgumentNullException("IV");
// Declare the string used to hold
// the decrypted text.
string plaintext = null;
// Create an Aes object
// with the specified key and IV.
using (Aes aesAlg = Aes.Create())
{
aesAlg.Key = Key;
aesAlg.IV = IV;
// Create a decryptor to perform the stream transform.
ICryptoTransform decryptor = aesAlg.CreateDecryptor(aesAlg.Key, aesAlg.IV);
// Create the streams used for decryption.
using (MemoryStream msDecrypt = new MemoryStream(cipherText))
{
using (CryptoStream csDecrypt = new CryptoStream(msDecrypt, decryptor, CryptoStreamMode.Read))
{
using (StreamReader srDecrypt = new StreamReader(csDecrypt))
{
// Read the decrypted bytes from the decrypting stream
// and place them in a string.
plaintext = srDecrypt.ReadToEnd();
}
}
}
}
return plaintext;
}
}
}
Пример шифрования AES можно посмотреть на сайте.
Криптосистема RSA представляет собой ассиметричную систему шифрования. Асимметричное шифрование подразумевает под собой тот факт, что посторонним лицам может быть известен алгоритм шифрования, и, возможно открытый ключ, но неизвестен закрытый ключ, известный только получателю. Криптографические системы с открытым ключом в настоящее время широко применяются в различных сетевых протоколах, в частности, в протоколах TLS и его предшественнике SSL (лежащих в основе HTTPS), а так же SSH, PGP, S/MIME и т.д.
То есть для шифрования и дешифрирования необходимы различные ключи:
Открытый ключ используется для шифрования данных, а секретный ключ (закрытый) для их дешифрирования. Такой подход в этой криптографической системе дает возможность передавать ключ, который использовался для шифрования, передавать по открытому каналу, так как даже при получении злоумышленником открытого ключа, дешифрировать сообщение будет практически невозможно. Так же стоит учесть тот факт, что алгоритм шифрования RSA рассчитан на работу с длинной арифметикой, что соответственно объясняет невозможность подбора ключа для дешифрирования.
Шифрование исходного файла $X$ в RSA производится путем возведения в степень, равную открытому ключу $Kо$ по модулю большого числа $r$, где $X$ лежит в пределах от $0$ до $r$. То есть получаем следующее выражение для шифрования:
$$Y = E_{Kо}(X) = X^{Kо}\mod r.$$В приведенном выше выражении, $E_{Kо}$ алгоритм шифрования, $r$ - является результатом умножения двух простых больших чисел $p$ и $q$. Использование такого выражения для шифрования есть использование, так называемых, односторонних функций, которые обладают следующим свойством:
Под односторонностью понимается не теоретическая однонаправленность, а практическая невозможность вычислить обратное значение, используя современные вычислительные средства, за обозримый интервал времени. Процедура формирования параметров алгоритма RSA выглядит следующим образом:
Полученное значение будет являться закрытым ключом $Kс$.
Условия и ограничения для данных, вводимых пользователем (дополнительные проверки):
Получение секретного ключа K cосуществляется следующим образом: находится значение функции Эйлера от $r$, которое далее передается в функцию Евклида вместе со значением открытого ключа $Ко$.
Дешифрирование. Для расшифрования шифротекста необходимо воспользоваться значением $Kc$, а также необходимо знать значение $r$. То есть ключом будет являться пара значений - $(Kc, r)$. Другие же значения: $p$ и $q$ - хранятся в секрете. Так же пользователь, который будет пытаться произвести дешифрацию файла, будет иметь при себе значение открытого ключа $Ko$. Дешифрирование производится путём возведения шифротекста в степень закрытого ключа $Kc$ по модулю $r$. Получение исходного текста из зашифрованного возможно за счет того, что обязано выполнятся свойство открытого и закрытого ключей, для которых должно выполняться равенство:
$$(Kо·Kc)\mod C(r) = 1,$$где $C(r)$ - функция Эйлера от $r$.
Если же какой-либо пользователь решит взломать данный шифр, то он столкнётся с необходимостью методом подбора определять искомое значение функции Эйлера, то есть раскладывать на простые множители большое число $r$. На сегодняшний день данная задача не имеет эффективного решения, а использование традиционных методов поиска множителей для чисел размерностью порядка $2^{2048}$ не позволяет осуществить взлом криптосистемы за разумное время. Именно числа порядка $2^{2048}$ рекомендуется использовать в данном алгоритме.
Пример шифрования RSA можно посмотреть на сайте.
При обмене электронными документами по сети связи возникает проблема аутентификации автора документа и самого документа, т.е. установления подлинности автора и отсутствия изменений в полученном документе. В обычной (бумажной) информатике эти проблемы решаются за счет того, что информация в документе и рукописная подпись автора жестко связаны с физическим носителем (бумагой). В электронных документах на машинных носителях такой связи нет.
Электронная цифровая подпись (ЭЦП) используется для аутентификации текстов, передаваемых по телекоммуникационным каналам. Функционально она аналогична обычной рукописной подписи и обладает ее основными достоинствами:
Цифровая подпись представляет собой относительно небольшое количество дополнительной цифровой информации, передаваемой вместе с подписываемым текстом. Система ЭЦП включает две процедуры: 1) постановки подписи; 2) проверки подписи. В процедуре постановки подписи используется секретный ключ отправителя сообщения, в процедуре проверки подписи – открытый ключ отправителя.
При формировании ЭЦП отправитель прежде всего вычисляет хэшфункцию $h(M)$ подписываемого текста $M$. Вычисленное значение хэшфункции $h(M)$ представляет собой один короткий блок информации $m$, характеризующий весь текст $M$ в целом. Хэш-функция предназначена для сжатия подписываемого документа $M$ до нескольких десятков или сотен бит. Хэш-функция $h(M)$ принимает в качестве аргумента сообщение (документ) $M$ произвольной длины и возвращает хэш-значение $h(M) = m$ фиксированной длины. Обычно хэшированная информация является сжатым двоичным представлением основного сообщения произвольной длины. Значение хэш-функции $h(M)$ сложным образом зависит от документа $M$ и не позволяет восстановить сам документ $M$.
Затем число $m$ шифруется секретным ключом отправителя. Получаемая при этом пара чисел представляет собой ЭЦП для данного текста $M$. При проверке ЭЦП получатель сообщения снова вычисляет хэшфункцию $m = h(M)$ принятого по каналу сообщения $M$, после чего при помощи открытого ключа отправителя проверяет, соответствует ли полученная подпись вычисленному значению $m$ хэш-функции.
Функция $h(M)$ – является хэш-функцией, если она удовлетворяет следующим условиям:
Из определения следует, что для любой хэш-функции есть тексты близнецы – имеющие одинаковое значение хэш-функции, так как мощность множества аргументов неограниченно больше мощности множества значений. Такой факт получил название «эффект дня рождения». Наиболее известные из хэш-функций – MD2, MD4, MD5 и SHA. Три алгоритма серии MD разработаны Ривестом в 1989-м, 90-м и 91-м годах соответственно. Все они преобразуют текст произвольной длины в 128-битную сигнатуру.
Алгоритм MD2 предполагает:
Алгоритм MD4 предусматривает:
В алгоритме MD4 довольно быстро были найдены «дыры», поэтому он был заменен алгоритмом MD5, в котором каждый блок участвует не в трех, а в четырех различных циклах.
Алгоритм SHA (Secure Hash Algorithm) разработан NIST (National Institute of Standard and Technology) и повторяет идеи серии MD. В SHA используются тексты более 264 бит, которые закрываются сигнатурой длиной 160 бит. Принципиальным моментом в системе ЭЦП является невозможность подделки ЭЦП пользователя без знания его секретного ключа подписывания. В качестве подписываемого документа может быть использован любой файл. Подписанный файл создается из неподписанного путем добавления в него одной или более электронных подписей. Каждая подпись содержит следующую информацию:
Технология применения системы ЭЦП предполагает наличие сети абонентов, посылающих друг другу подписанные электронные документы. Для каждого абонента генерируется пара ключей: секретный и открытый. Секретный ключ хранится абонентом в тайне и используется им для формирования ЭЦП. Открытый ключ известен всем другим пользователям и предназначен для проверки ЭЦП получателем подписанного электронного документа. Иначе говоря, открытый ключ является необходимым инструментом, позволяющим проверить подлинность электронного документа и автора подписи. Открытый ключ не позволяет вычислить секретный ключ.
Для генерации пары ключей (секретного и открытого) в алгоритмах ЭЦП, как и в асимметричных системах шифрования, используются разные математические схемы, основанные на применении однонаправленных функций. Эти схемы разделяются на две группы. В основе такого разделения лежат известные сложные вычислительные задачи:
Первой и наиболее известной во всем мире конкретной системой ЭЦП стала система RSA. Другой системой электронной цифровой подписи является система Эль Гамаля (EGSA). Название EGSA происходит от слов El Gamal Signature Algorithm (алгоритм цифровой подписи Эль Гамаля). Идея EGSA основана на том, что для обоснования практической невозможности фальсификации цифровой подписи может быть использована более сложная вычислительная задача, чем разложение на множители большого целого числа, – задача дискретного логарифмирования. Кроме того, Эль Гамалю удалось избежать явной слабости алгоритма цифровой подписи RSA, связанной с возможностью подделки цифровой подписи под некоторыми сообщениями без определения секретного ключа.
Из-за проблем с MD5/SHA1 Корпорация Майкрософт рекомендует использовать SHA256 или SHA512.
Пример простой создания и проверки цифровых подписей с использованием открытых ключей RSA ня языке C#
using System;
using System.Security.Cryptography;
using System.Text;
class Class1
{
public static byte[] GetHash(string inputString)
{
using (HashAlgorithm algorithm = SHA256.Create())
return algorithm.ComputeHash(Encoding.UTF8.GetBytes(inputString));
}
static void Main()
{
string inputString = "Maecenas ultricies pretium justo id fringilla. Pellentesque leo tortor, convallis vitae neque in, pretium condimentum metus. Sed accumsan pharetra augue, non hendrerit libero iaculis a. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Maecenas tincidunt volutpat finibus. Phasellus sit amet tempor tortor, ac tincidunt orci. Nunc facilisis sed ligula a porttitor.";
//The hash value to sign.
byte[] hashValue = GetHash(inputString);
//The value to hold the signed value.
byte[] signedHashValue;
//Generate a public/private key pair.
RSA rsa = RSA.Create();
//Create an RSAPKCS1SignatureFormatter object and pass it the
//RSA instance to transfer the private key.
RSAPKCS1SignatureFormatter rsaFormatter = new RSAPKCS1SignatureFormatter(rsa);
//Set the hash algorithm to SHA256.
rsaFormatter.SetHashAlgorithm("SHA256");
//Create a signature for hashValue and assign it to
//signedHashValue.
signedHashValue = rsaFormatter.CreateSignature(hashValue);
Console.WriteLine("Original: {0}", System.Text.Encoding.ASCII.GetString(hashValue, 0, hashValue.Length));
Console.WriteLine("Original: {0}", BitConverter.ToString(hashValue));
Console.WriteLine("Signed: {0}", System.Text.Encoding.ASCII.GetString(signedHashValue, 0, signedHashValue.Length));
Console.WriteLine("Signed: {0}", BitConverter.ToString(signedHashValue));
Console.WriteLine("RSA PrivateKey: {0}", BitConverter.ToString(rsa.ExportRSAPrivateKey()));
Console.WriteLine("RSA KeyInfo P: {0}", BitConverter.ToString(rsa.ExportParameters(true).P));
Console.WriteLine("RSA KeyInfo Q: {0}", BitConverter.ToString(rsa.ExportParameters(true).Q));
Console.WriteLine("RSA PublicKey: {0}", BitConverter.ToString(rsa.ExportRSAPublicKey()));
//Проверка подписи
RSAParameters rsaKeyInfo;
rsaKeyInfo = rsa.ExportParameters(true);
Console.WriteLine("RSA KeyInfo Modulus: {0}", BitConverter.ToString(rsaKeyInfo.Modulus));
Console.WriteLine("RSA KeyInfo Exponent: {0}", BitConverter.ToString(rsaKeyInfo.Exponent));
RSA rsa_test = RSA.Create();
rsa_test.ImportParameters(rsaKeyInfo);
RSAPKCS1SignatureDeformatter rsaDeformatter = new RSAPKCS1SignatureDeformatter(rsa_test);
rsaDeformatter.SetHashAlgorithm("SHA256");
if (rsaDeformatter.VerifySignature(hashValue, signedHashValue))
{
Console.WriteLine("The signature is valid.");
}
else
{
Console.WriteLine("The signature is not valid.");
}
}
}
Российский стандарт электронной цифровой подписи определен ГОСТ 34.10-2018. Информационная технология. Криптографическая защита информации. Процессы формирования и проверки электронной цифровой подписи.
Пошаговое руководство для создания криптографического приложения на языке C# приведено на сайте Microsoft.
Как бы ни была сложна и надежна сама криптосистема, она основана на использовании ключей. Если для обеспечения конфиденциального обмена информацией между двумя пользователями процесс обмена ключами тривиален, то в системе, где количество пользователей составляет десятки и сотни управление ключами, – это серьезная проблема.