Уравнение первого закона термодинамики для потока имеет вид:
$$q_{12}=(h_2-h_1)+\frac{w_2^2-w_1^2}{2}+g·(z_2-z_1)+l_{техн}+l_{тр},$$или в дифференциальной форме:
$$\mathrm{d}q=\mathrm{d}h+w\mathrm{d}w+g\mathrm{d}z+\mathrm{d}l_{техн}+\mathrm{d}l_{тр}.$$Если рассматриваемый участок потока находится на одном геометрическом уровне, то $\mathrm{d}z=0$, если поток не производит технической работы и эта работа не подводится к нему, то $\mathrm{d}l_{техн}=0$, если отсутствует вязкое трение на стенках канала, то $\mathrm{d}l_{тр}=0$.
Очевидно, что для этого случая:
$$\mathrm{d}q=\mathrm{d}h+w\mathrm{d}w.$$Для подавляющего большинства технически важных задач наибольший интерес представляет рассмотрение случая адиабатного течения, т.е. течения без подвода теплоты извне и отвода ее. Для адиабатного потока можно записать:
$$\mathrm{d}h+w\mathrm{d}w=0.$$Интегрируя уравнение между двумя точками потока, получаем:
$$h_1-h_2=\frac{w_2^2-w_1^2}{2}.$$откуда
$$w_2=\sqrt{2·(h_1-h_2 )+w_1^2}=\sqrt{2·\intop_{p_2}^{p_1} v\mathrm{d}p+w_1^2}.$$Cкоростью звука называют скорость распространения в среде малых возмущений (малыми называются такие возмущения среды, в которых местное изменение давления среды в точке возмущения, т.е. амплитуда давления, пренебрежимо мало по сравнению с общим давлением).
Cкорость распространения малых возмущений (скорость звука в среде) определяется по уравнению Лапласа:
$$a=\sqrt{-v^2·\left(\frac{\partial p}{\partial v}\right)_s}.$$Поскольку величины $v$ и $\left(\frac{\partial p}{\partial v}\right)_s$ являются функциями состояния, скорость звука $a$, определяемая уравнением Лапласа, также является термодинамической функцией состояния.
С учетом того, что показатель адиабаты можно представить как:
$$k=-\frac{v}{p}·\left(\frac{\partial p}{\partial v}\right)_s,$$то
$$a=\sqrt{k·p·v}.$$С учетом уравнения Клапейрона для идеального газа можно получить:
$$a=\sqrt{k·R·T}.$$Cкорость звука в идеальном газе зависит для данного газа только от температуры, а для реального газа скорость звука зависит не только от температуры, но и от давления.
Истечение из суживающихся сопл. Для увеличения скорости потока применяют специально спрофилированные каналы, называемые соплами. Сопло представляет собой канал, суживающийся в направлении движения потока.
Для случая адиабатного истечения идеального газа можно получить:
$$w_2=\sqrt{2·\intop_{p_2}^{p_1} v \mathrm{d}p+w_1^2}=\sqrt{2·\frac{k}{k-1}·p_1·v_1·\left( 1-\left( \frac{p_2}{p_1} \right)^{ \frac{k-1}{k} }+w_1^2 \right)}.$$Массовый расход газа определяется из выражения:
$$G=\frac{f_2·w_2}{v_2},$$где $v_2$ – удельный объем газа в выходном сечении сопла; $f_2$ – площадь выходного сечения сопла.
Заменяя в этом соотношении $v_2$ с помощью уравнения адиабаты получаем:
$$G=\frac{f_2}{v_1}·\left(\frac{p_2}{p_1}\right)^{\frac{1}{k}}·w_2$$или
$$G=\frac{f_2}{v_1}·\left(\frac{p_2}{p_1}\right)^{\frac{1}{k}}·\sqrt{(2·\frac{k}{k-1}·p_1·v_1·\left(1-\left(\frac{p_2}{p_1}\right)^{\frac{k-1}{k}}+w_1^2\right)}.$$Обозначив отношение давлений в сопле $ψ=\frac{p_2}{p_1}$, получим:
$$G=\frac{f_2}{v_1}·ψ^{\frac{1}{k}}·\sqrt{2·\frac{k}{k-1}·p_1·v_1·\left(1-ψ^{\frac{k-1}{k}}\right)+w_1^2}.$$Отношение давлений $ψ$, при котором расход газа становится максимальным, называется критическим и равно:
$$ψ_{кр}=\left(\frac{2}{k+1}\right)^{\frac{k}{k-1}}.$$При $ψ_{кр} < ψ < 1$ скорость газа и расход растут с уменьшением $ψ$. Если уменьшить $ψ$ в диапазоне $0 < ψ < ψ_{кр}$, то расход не изменяется, оставаясь максимальным, а скорость также не изменяется, оставаясь равной критической скорости $w_{кр}$, которая равна местной скорости звука.
Сопло Лаваля. При течении газа (жидкости) в канале для любого сечения канала из соображений неразрывности потока справедливо уравнение:
$$G=\frac{f·w}{v}=const,$$где $G$ – постоянный массовый расход газа; $f$ – площадь сечения канала; $w$ – скорость газа и $v$ – удельный объем газа в данном сечении канала.
Это уравнение называют в гидродинамике уравнением неразрывности. Логарифмируя последнее уравнение, получаем:
$$\ln f+\ln w- \ln v=const.$$Дифференцируя это соотношение, получаем уравнение неразрывности в дифференциальной форме:
$$\frac{\mathrm{d}f}{f}=\frac{\mathrm{d}v}{v}-\frac{\mathrm{d}w}{w}.$$С учетом того, что:
$$w\mathrm{d}w=-v\mathrm{d}p$$и
$$\frac{\mathrm{d}v}{v}=-\frac{\mathrm{d}p}{k·p},$$получаем:
$$\frac{\mathrm{d}f}{f}=-\frac{\mathrm{d}p}{k·p}-\left(-\frac{v\mathrm{d}p}{w^2}\right)=\frac{k·v·p-w^2}{k·p·w^2} \mathrm{d}p.$$C учетом $a=\sqrt{k·v·p} уравнение преобразуется к виду:
$$\frac{\mathrm{d}f}{f}=\frac{a^2-w^2}{k·p·w^2} \mathrm{d}p=\frac{1}{k·p}·\left(\frac{1}{M^2}-1\right)\mathrm{d}p,$$где $M=\frac{w}{a}$ – так называемое число Маха (отношение скорости течения к местной скорости звука).
Значение $М < 1$ соответствует течению с дозвуковыми скоростями ($w < a$), а $М > 1$ — течению со скоростями, превышающими скорость звука ($w > a$).
Подставляя выражение для $\mathrm{d}p$ из уравнения $w\mathrm{d}w=-v\mathrm{d}p$, получаем уравнение, связывающее изменение площади сечения канала с изменением скорости потока и с числом Маха:
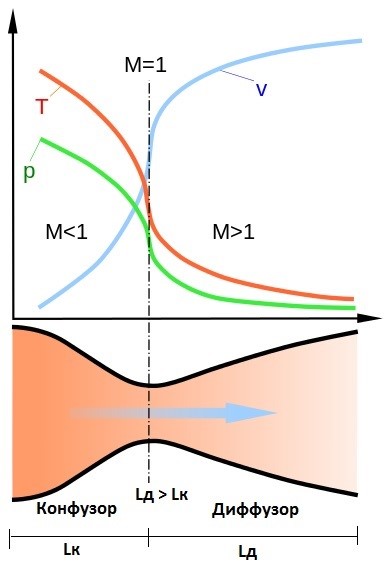
$$(M^2-1)\frac{\mathrm{d}w}{w}=\frac{\mathrm{d}f}{f}.$$Из этих уравнений следует, что при дозвуковых скоростях течения ($М < 1$) сужение канала ($\mathrm{d}f < 0$) соответствует снижению давления в потоке вдоль канала ($\mathrm{d}p < 0$), т.е. случаю обычного суживающегося сопла. В этом случае ($М < 1$) при сужении канала, как и следовало ожидать, скорость потока увеличивается ($\mathrm{d}w>0$). Если же при дозвуковом течении канал расширяется ($\mathrm{d}f>0$), то скорость потока снижается ($\mathrm{d}w < 0$), а давление в потоке вдоль канала возрастает ($\mathrm{d}p > 0$). Расширяющиеся каналы, применяемые для торможения дозвукового потока, т.е. для превращения кинетической энергии потока в потенциальную энергию сжатого газа, носят название диффузоров.
При $М > 1$ течение в расширяющемся канале ($\mathrm{d}f > 0$) происходит с уменьшением давления вдоль потока ($\mathrm{d}p < 0$) и с увеличением скорости ($\mathrm{d}w > 0$) и, наоборот, сверхзвуковой поток в суживающемся канале ($\mathrm{d}f < 0$) замедляется ($\mathrm{d}w < 0$), а его давление возрастает ($\mathrm{d}p > 0$). Таким образом, профили сопла и диффузора для сверхзвукового потока «меняются местами» – сверхзвуковое сопло представляет собой расширяющийся канал, а сверхзвуковой диффузор – суживающийся канал.
Из этого анализа становится очевидным, как осуществить дальнейшее ускорение потока, который приобрел на выходе из суживающегося сопла звуковую скорость. Для этого сопло должно быть спрофилировано таким образом, чтобы канал суживался до тех пор, пока давление в канале не станет равным критическому давлению истечения. За этим сечением канал должен быть выполнен расширяющимся. В соответствии со сказанным выше поток перейдет через скорость звука и будет продолжать ускоряться в расширяющейся части сопла. Таким образом, для ускорения потока будет использован весь перепад давления от давления на входе в сопло до давления среды, а не только часть этого перепада до критического давления, реализуемая в суживающемся дозвуковом сопле.
Такое комбинированное сопло, состоящее из суживающейся и расширяющейся частей, впервые было применено для получения сверхзвуковых скоростей истечения газа шведским инженером К. Лавалем в 80-х годах XIX столетия, поэтому сопла такого типа называют соплами Лаваля.
Расчет суживающейся части сопла Лаваля проводится так же, как и обычного суживающегося дозвукового сопла. Площадь минимального сечения сопла определяется по заданному расходу уравнением:
$$f_{мин}=\frac{G·v_{мин}}{a}.$$При прохождении газа или пара через сужение канала (диафрагма, вентиль, клапан и т. п.) происходит снижение его давления без совершения внешней работы, поскольку в реальных условиях течение газа или жидкости в каналах всегда сопровождается потерями энергии на преодоление трения, обусловленными вязкостью газа, шероховатостью стенок канала и т.д.. Этот необратимый процесс называется дросселированием.
Поскольку процесс дросселирования быстротечен, его можно считать, идущим без теплообмена с окружающей средой $q=0$. В этом процессе практически отсутствует изменение кинетической энергии потока, т.к. площади сечений канала обычно одинаковы, а увеличение удельного объема газа за счет снижения давления уменьшает кинетическую энергию потока на очень малую величину по отношению к численным значениям энтальпий, поэтому считают, что $w_1≈w_2$. Уравнение первого закона термодинамики для 1 и 2 сечений канала (до и после дросселирования) будет иметь вид:
$$h_1-h_2=\frac{w_2^2}{2}–\frac{w_1^2}{2},$$для нашего процесса $w_1≈w_2$, тогда окончательно имеем:
$$h_1≈h_2.$$Таким образом, в результате адиабатного процесса дросселирования энтальпия вещества в начале и конце процесса одинакова.
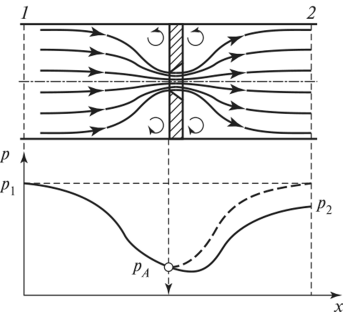
Надо иметь в виду, что при течении через сужение канала на участке ускорения потока энтальпия уменьшается, а на участке торможения – возрастает, достигая начального значения. Локальные изменения энтальпии при дросселировании практического интереса не представляют. Важен конечный результат, из которого следует, что в результате дросселирования энтальпия газа не меняется.
Изменение температуры при дросселировании связано с тем, что в каждом реальном газе действуют силы притяжения и отталкивания между молекулами. При дросселировании происходит расширение газа, сопровождающееся увеличением расстояния между ними. Все это приводит к уменьшению внутренней энергии рабочего тела, связанному с затратой работы, что, в свою очередь, приводит к изменению температуры. При дросселировании идеального газа, его температура не меняется.