1. В закрытом сосуде емкостью $V = 300$ л содержится $3$ кг газа при давлении $p_1 = 8$ ат и температуре $t_1 = 20$ °C. Определить давление (ат) и удельный объем после охлаждения воздуха до $0$ °C.

2. В закрытом сосуде заключен газ при разрежении $p_1 = 6.7$ кПа и температуре $t_1 = 70$ °C. Показания барометра – $742$ мм.рт.ст. До какой температуры нужно охладить газ при том же атмосферном давлении, чтобы разрежение стало $p_2 = 13.3$ кПа?

3. В закрытом сосуде емкостью $V = 0.6$ м3 содержится азот при давлении (абсолютном) $p_1 = 0.5$ МПа и температуре $t_1 = 20$ °C. В результате охлаждения сосуда азот, содержащийся в нем, теряет $105$ кДж. Определить, какие давление и температура устанавливаются в сосуде после охлаждения.

4. Сосуд емкостью $90$ л содержит углекислый газ при абсолютном давлении $0.8$ МПа и температуре $30$ °C. Определить количество теплоты, которое необходимо сообщить газу при $v = const$, чтобы давление поднялось до $1.6$ МПа.
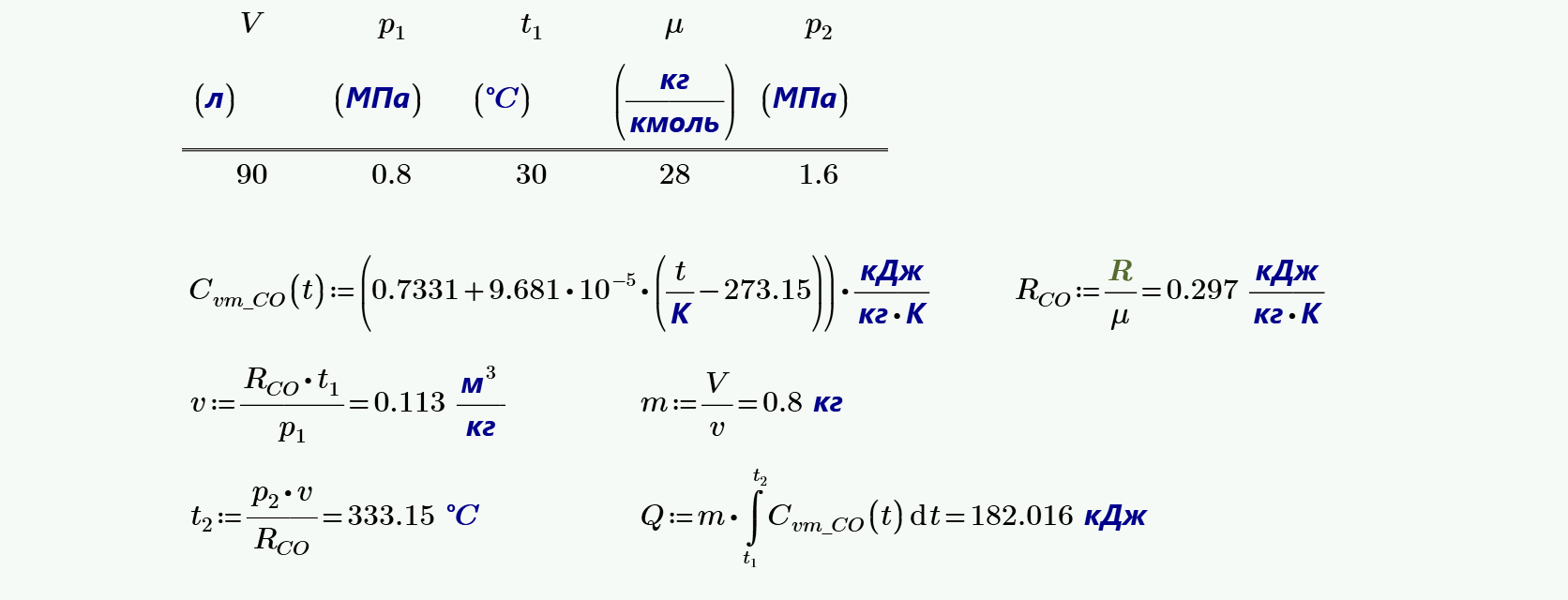
5. Какое количество теплоты необходимо затратить, чтобы нагреть $2$ м3 воздуха при постоянном избыточном давлении $p = 2$ ат от $t_1 = 120$ °C до $t_2 = 450$ °C? Какую работу при этом совершит воздух? Атмосферное давление принять равным $750$ мм.рт.ст., учесть зависимость теплоемкости от температуры.

6. В установке воздушного отопления внешний воздух при $t_1 = – 15$ °C нагревается в калорифере при $p = const$ до $60$ °C. Какое количество теплоты надо затратить для нагревания $1000$ м3 наружного воздуха? Давление воздуха считать равным $755$ мм.рт.ст.

7. Уходящие газы котельной установки проходят через воздухоподогреватель. Начальная температура газов $t_{г1} = 300$ °C, конечная $t_{г2} = 160$ °C; расход газов равен $900$ кг/ч. Начальная температура воздуха составляет $t_{в1} = 15$ °C, а расход его равен $800$ кг/ч. Определить температуру нагретого воздуха $t_{в2}$, если потери тепла в воздухоподогревателе составляет $4$ %. Средние теплоемкости для газов и воздуха принять соответственно равными $1.0467$ и $1.0048$ кДж/(кгּ К).
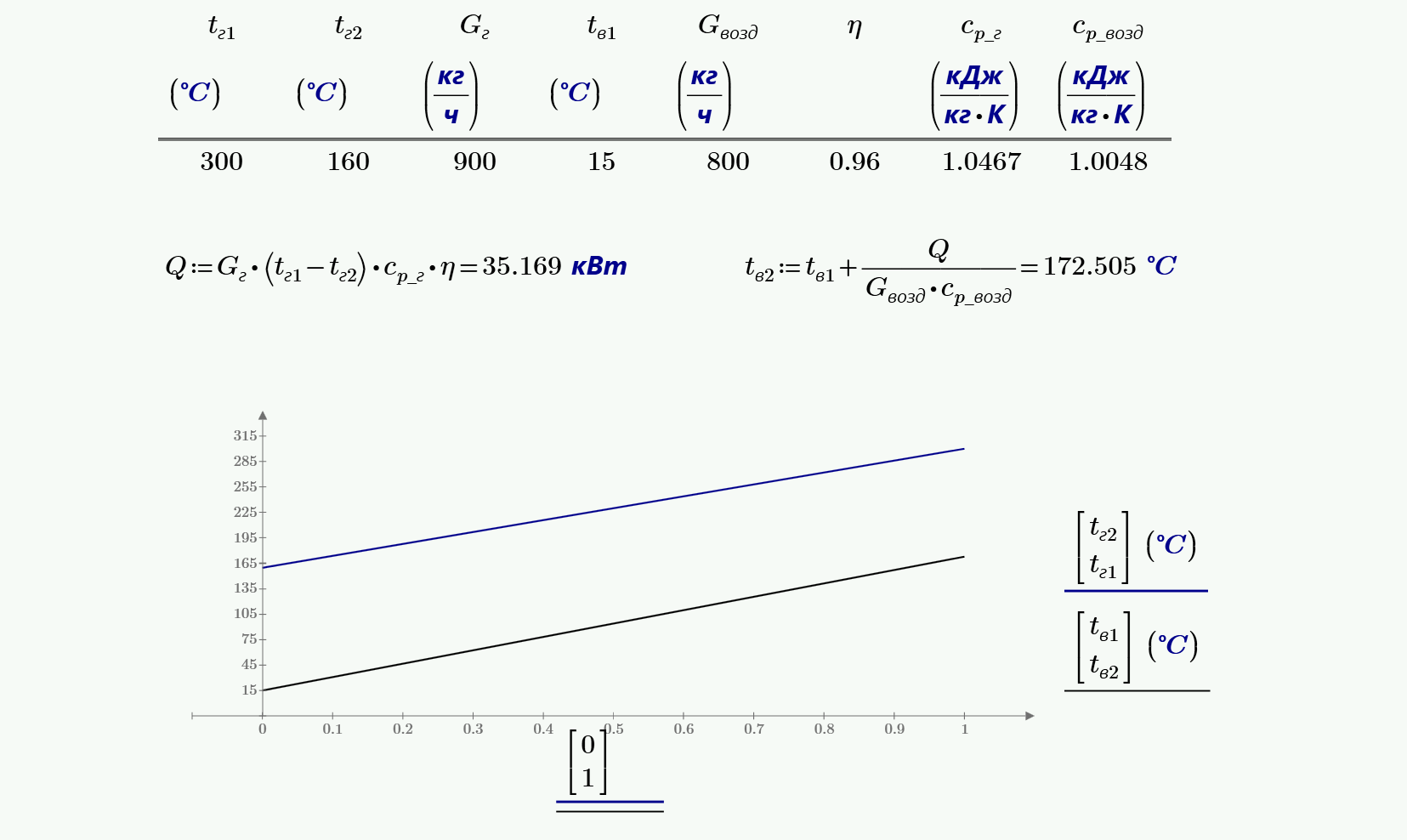
8. При сжигании в топке парового котла каменного угля объем продуктов сгорания составляет $V_н = 11.025$ м3/кг (объем при нормальных условиях, приходящийся на 1 кг топлива). Анализ продуктов сгорания показывает следующий их объемный состав: $CO = 10$ %; $O2 = 8$ %; $H2O = 10$ %; $N2 = 72$ %. Определить количество теплоты, теряемой с уходящими газами (в расчете на $1$ кг топлива), если на выходе из котла температура газов равна $180$ °C, а температура окружающей среды $20$ °C. Давление продуктов сгорания принять равным атмосферному. Учесть зависимость теплоемкости от температуры.

9. Воздух в количестве $1$ кг при температуре $t = 30$ °C и начальном давлении $p_1 = 0.1$ МПа изотермически сжимается до конечного давления $p_2 = 1$ МПа. Определить конечный объем, затрачиваемую работу изменения объема и количество теплоты, отводимой от газа.

10. Воздух в количестве $12$ кг при температуре $t = 27$ °C изотермически сжимается до тех пор, пока давление не становится равным $4$ МПа. На сжатие затрачивается работа $L = –6$ МДж. Найти начальные давление и объем, конечный объем и теплоту, отведенную от воздуха.

11. Воздух в количестве $0.5$ кг изотермически расширяется от давления $p_1 = 100$ ат до $p_2$. Определить давление $p_2$ в ат, работу изменения объема $L_{1-2}$ и отведенную теплоту $Q_{1-2}$, если $\frac{v_2}{v_1} = 5$ и $t_1 = 30$ °C.
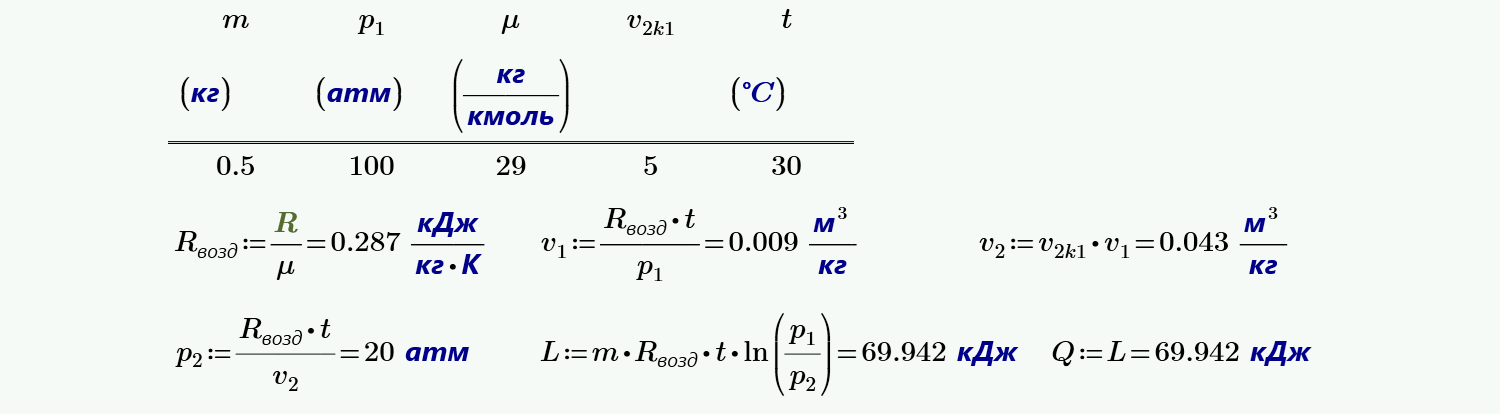
12. В идеально охлаждаемом компрессоре происходит изотермическое сжатие углекислого газа. В компрессор поступает $700$ м3/ч газа (приведенного к нормальным условиям) при $p_1 = 0.095$ МПа и $t_1 = 47$ °C. Давление за компрессором $p_2 = 0.8$ МПа. Найти теоретическую мощность приводного двигателя $N_0$ (кВт) и теоретический расход $M_в$ охлаждающей компрессор воды (в кг/ч), если она нагревается в системе охлаждения на $Δt = 15$ °C.

13. Воздух при температуре $t_1 = 20$ °C должен быть охлажден посредством адиабатного расширения до температуры $t_2 = –30$ °C. Конечное давление воздуха при этом должно составлять $0.1$ МПа. Определить начальное давление воздуха $p_1$ и работу расширения $1$ кг воздуха.

14. Воздух при температуре $120$ °C изотермически сжимается так, что его объем становится равным $0.25$ начального, а затем расширяется по адиабате до начального давления. Определить температуру воздуха в конце адиабатного расширения. Представить процессы расширения и сжатия в диаграммах pv и Ts.
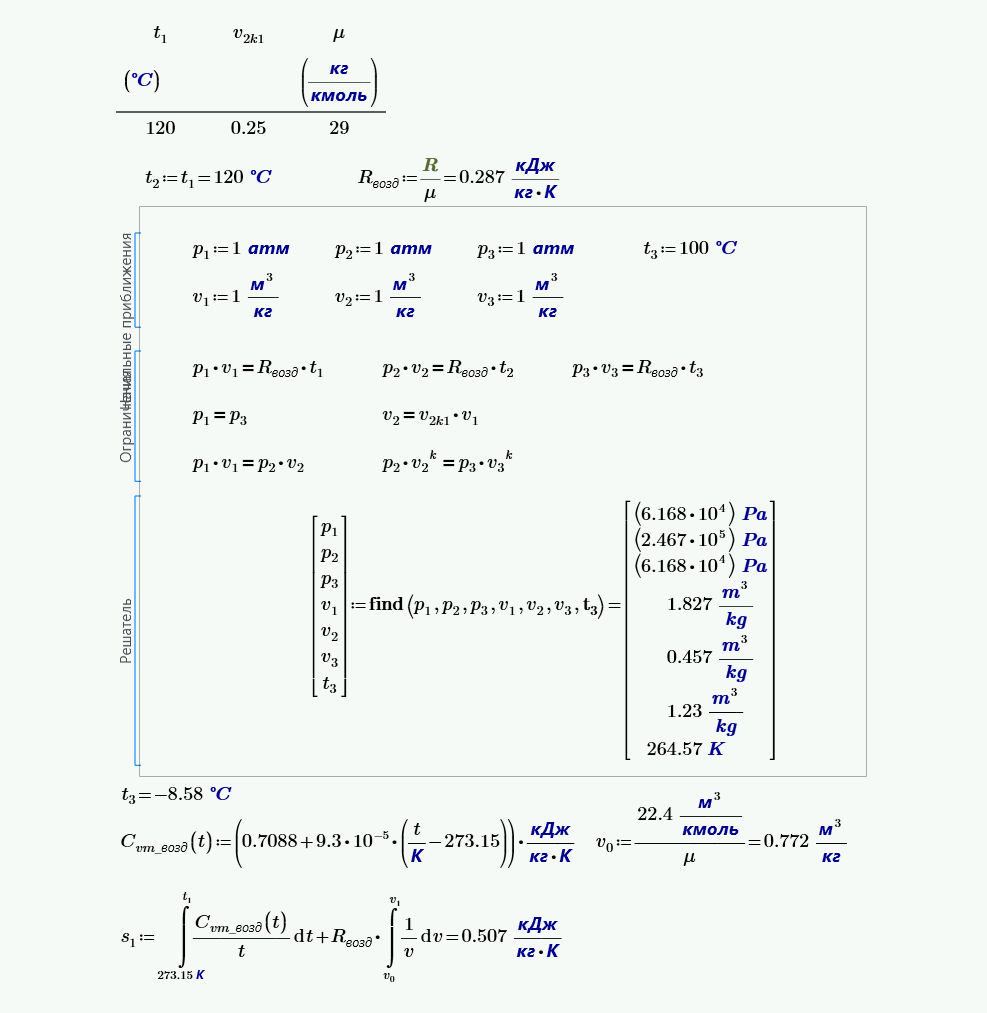
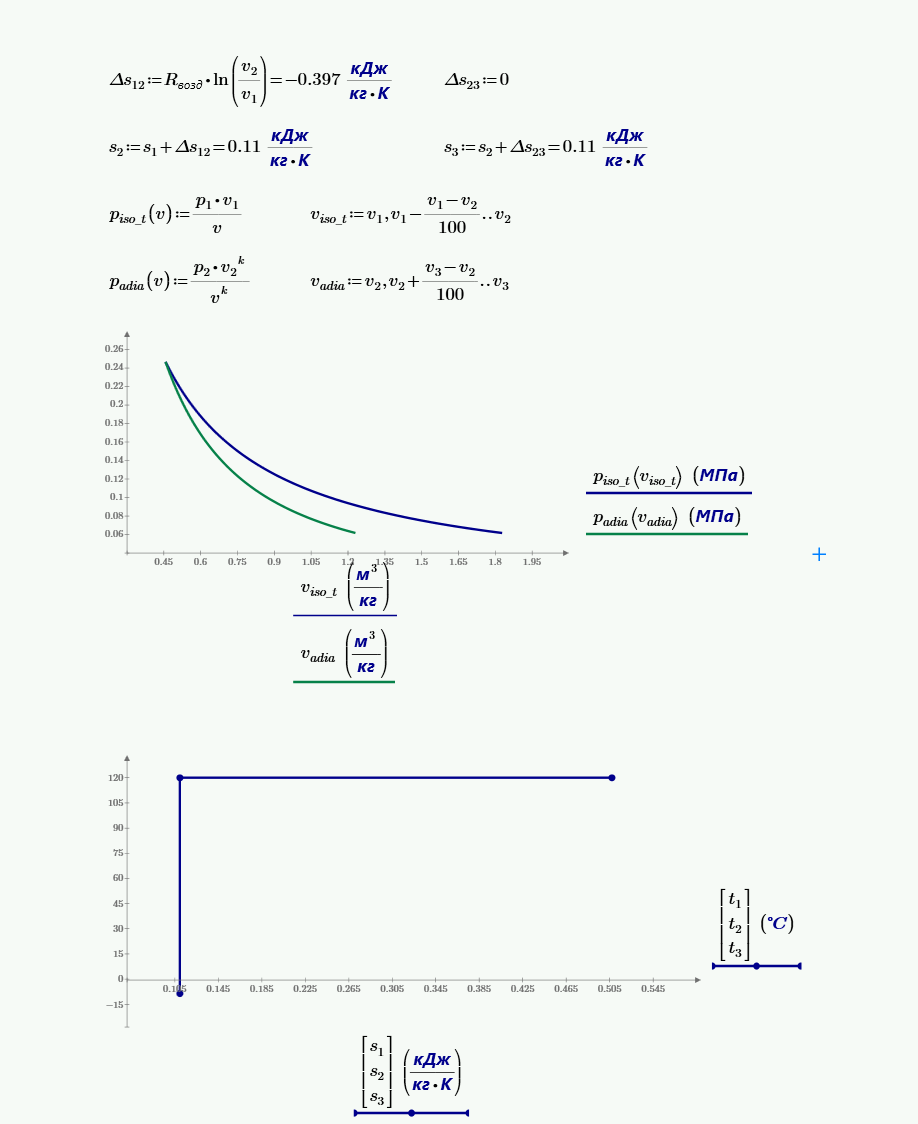
15. При адиабатном расширении $1$ кг воздуха $K = 1.40 = сonst$ температура его падает на $100$ K. Какова полученная в процессе расширения работа и сколько теплоты следовало бы подвести к воздуху, чтобы ту же работу получить в изотермическом процессе?
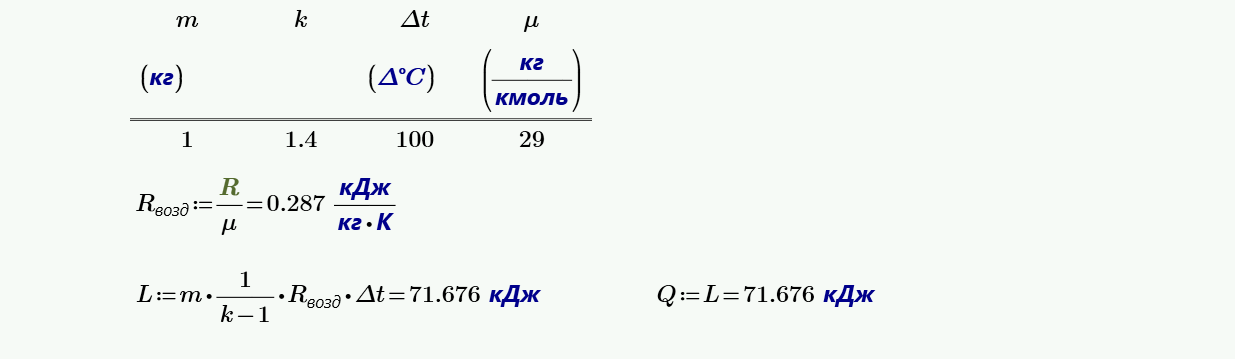
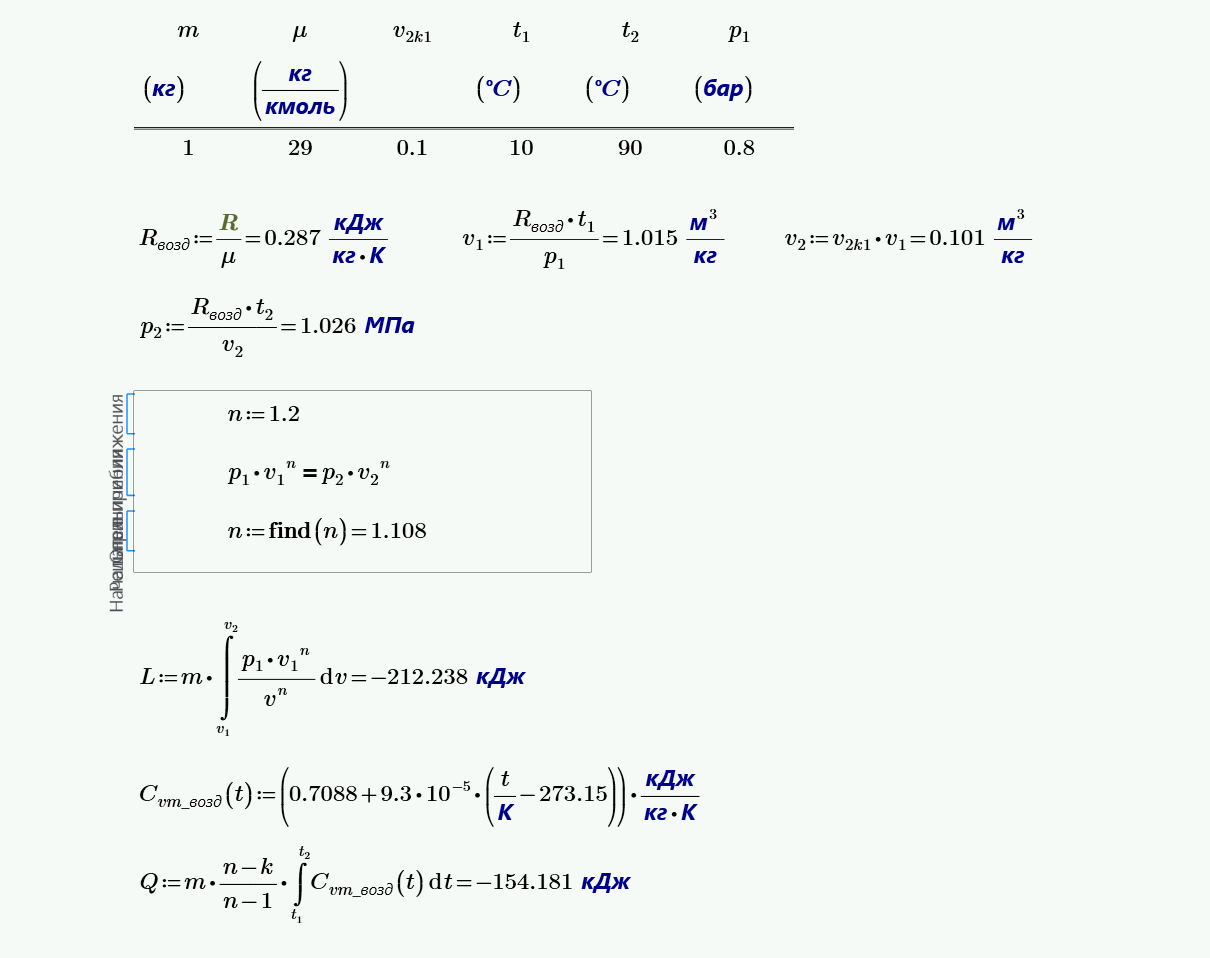
16. Воздух в количестве $1$ кг политропно расширяется от $12$ до $2$ ат, причем объем его увеличился в $4$ раза; начальная температура воздуха равна $120$ °C. Определить показатель политропы, начальный и конечный объемы, конечную температуру и работу расширения.

17. При политропном сжатии $1$ кг воздуха до объема $v_2 = 0.1ּ v_1$ температура поднялась с $10$ до $90$ °C. Начальное давление равно $0.8$ бар; $R = 287$ Дж/(кгּ K). Определить показатель политропы, конечные параметры газа, работу сжатия и количество отведенной наружу теплоты.
18. Воздух в компрессоре сжимается по политропе $n = 1.25$ от $1$ до $8$ бар; начальная температура воздуха $5$ °C. После сжатия воздух проходит через холодильник, охлаждаемый холодной водой, начальная температура которой $t_1 = 10$ °C, а конечная равна $t_2 = 18$ °C. Определить часовой расход охлаждающей воды, если производительность компрессора $1000$ мн3/ч при нормальных физических условиях, а воздух в холодильнике изобарно охлаждается до $30$ °C.

19. В воздушном двигателе воздух в количестве $1$ кг расширяется от $p_1 = 10$ ат до $p_2 = 1$ ат. Расширение может произойти изотермически, адиабатно и политропно с показателем политропы $n = 1.2$. Сравнить работы расширения и определить конечные параметры воздуха по этим трем процессам; начальная температура воздуха $t_1 = 227$ °C. Представить процессы на диаграмме pv.

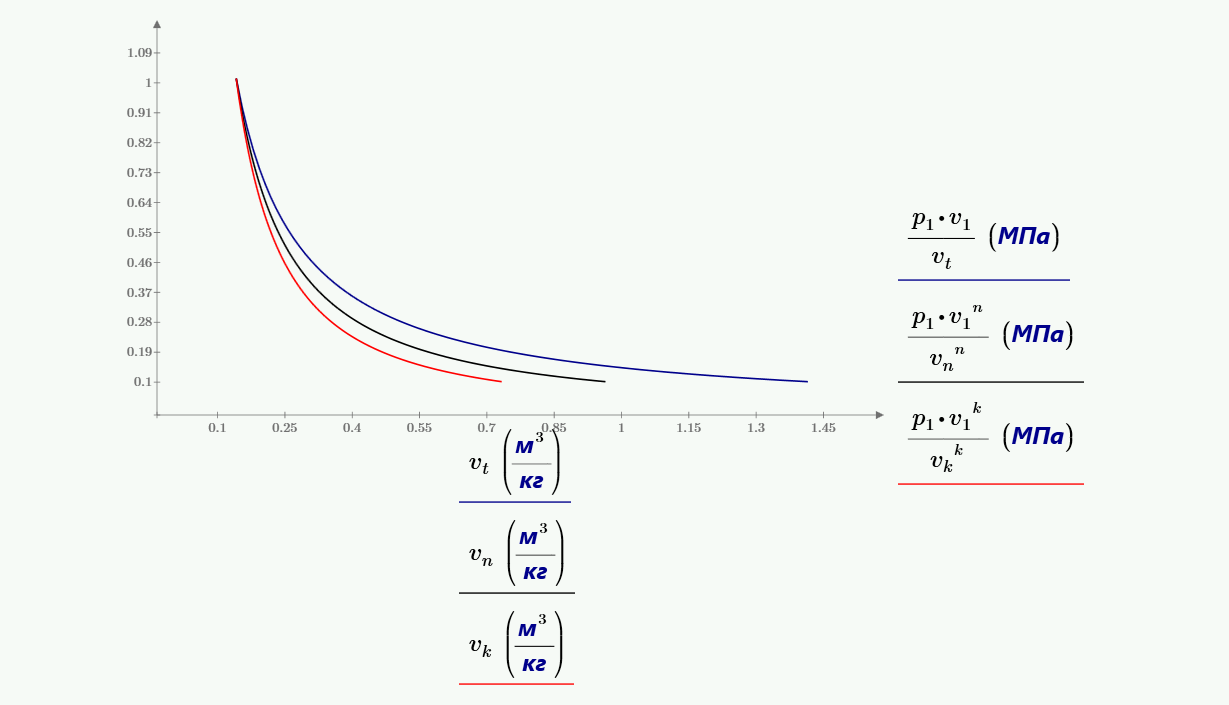
20. В процессе политропного расширения воздуху сообщается $70$ кДж теплоты. Найти изменение внутренней энергии воздуха и произведенную работу, если объем воздуха увеличился в $8$ раз, а давление его уменьшилось в $10$ раз.
