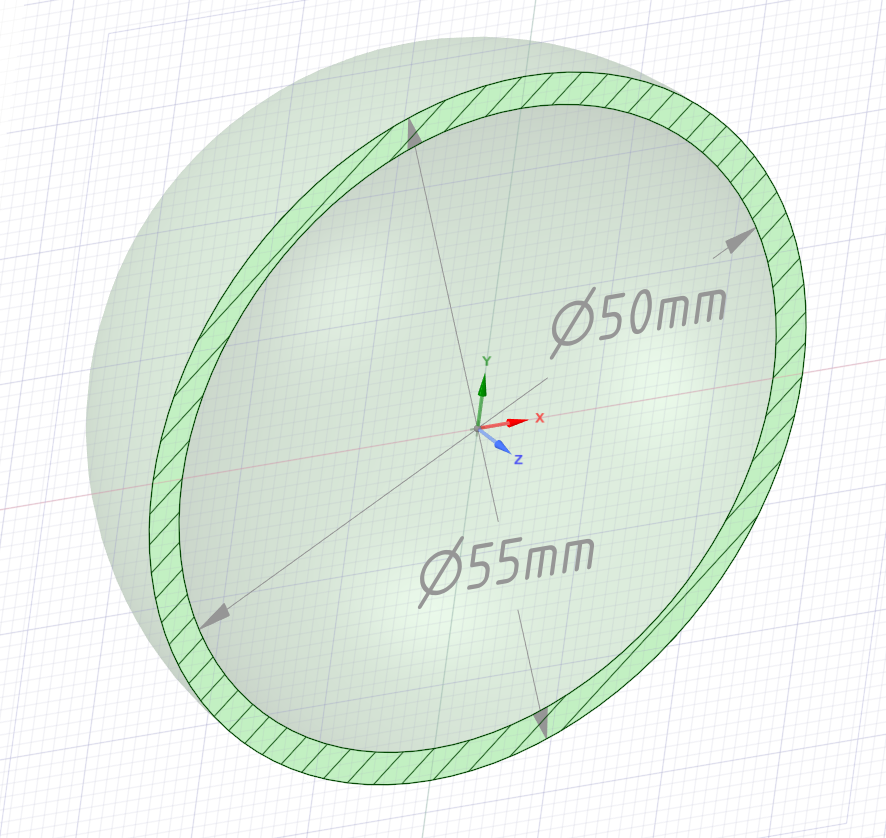
Определить потери теплоты шара, внутренним диаметром $d_1 = 50$ мм и наружным $d_2 = 55$ мм, и температуры их поверхностей. Коэффициент теплопроводности материала $\lambda = 45$ Вт/м·К. Коэффициент теплоотдачи от жидкости к внутренней поверхности $\alpha_1 = 10^4$ Вт/м2·К, к наружной поверхности $\alpha_2 = 10^4$ Вт/м2·К, температура жидкости внутри $t_{ж1} = 200$ °C, снаружи $t_{ж2} = 150$ °C.
Решить задачу для двух случаев: а) образец не изолирован; б) на образец наложена тепловая изоляция толщиной $\delta_{из} = 15$ мм. с коэффициентом теплопроводности $\lambda_{из} = 0.01$ Вт/м·К.
Оценить эффективность тепловой изоляции.
Записывается система уравнений:
$$Q = \pi·\alpha_1·d_1^2·(t_{ж1}-t_1);$$ $$Q = \frac{2·\pi·\lambda·(t_1-t_2)}{\frac{1}{d_1} - \frac{1}{d_2}};$$ $$Q = \pi·\alpha_2·d_2^2·(t_2-t_{ж2}).$$Обратите внимание! Вид уравнений зависит от геометрии тела и определяется общими уравнениями Фурье $Q=-\lambda·\mathrm{grad}(T)·F$ и Ньютона-Рихмана $Q = \alpha·\Delta T·F$.
После суммирования получим тепловой поток равный, Вт:
$$Q = \frac{\pi·(t_{ж1}-t_{ж2})}{\frac{1}{\alpha_1·d_1^2}+\frac{1}{2·\lambda}·\left(\frac{1}{d_1}-\frac{1}{d_2}\right)+\frac{1}{\alpha_2·d_2^2}} = \frac{\pi·(200-150)}{\frac{1}{10^4·0.050^2}+\frac{1}{2·45}·\left(\frac{1}{0.050}-\frac{1}{0.055}\right)+\frac{1}{10^4·0.055^2}} = 1684.$$Находим температуры стенок,°C:
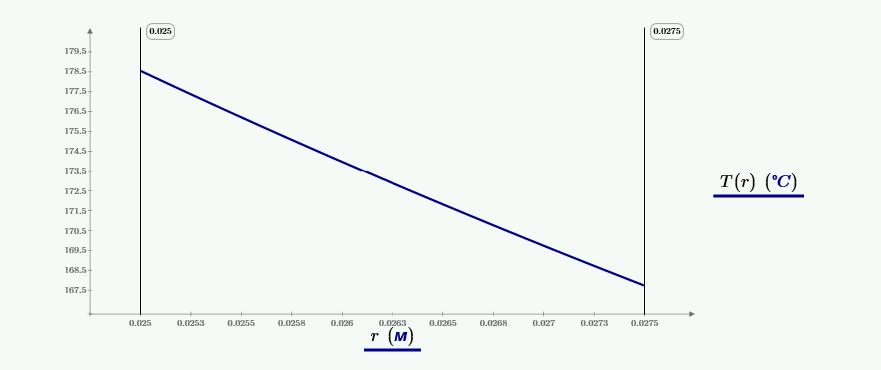
$$t_1 = -\frac{Q}{\alpha_1·\pi·d_1^2}+t_{ж1} = -\frac{1684}{10^4·\pi·0.050^2}+200 = 178,$$ $$t_2 = \frac{Q}{\alpha_2·\pi·d_2^2}+t_{ж2} = -\frac{1684}{10^4·\pi·0.055^2}+150 = 167.$$После наложения изоляции система уравнений дополняется уравнением теплопроводности для изоляции:
$$Q = \pi·\alpha_1·d_1^2·(t_{ж1}-t_1);$$ $$Q = \frac{2·\pi·\lambda·(t_1-t_2)}{\frac{1}{d_1} - \frac{1}{d_2}};$$ $$Q = \frac{2·\pi·\lambda·(t_1-t_{из})}{\frac{1}{d_2} - \frac{1}{d_{из}}};$$ $$Q = \pi·\alpha_2·d_{из}^2·(t_{из}-t_{ж2}).$$Обратите внимание! Количество уравнений всегда соответствует количеству процессов протекающих в системе. В данном случае процессов четыре - два процесса теплопроводности и два процесса теплоотдачи.
После суммирования получим тепловой поток равный, Вт:
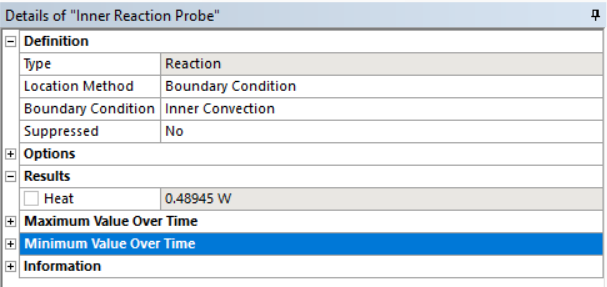
$$Q_{из} = \frac{\pi·(t_{ж1}-t_{ж2})}{\frac{1}{\alpha_1·d_1^2}+\frac{1}{2·\lambda}·\left(\frac{1}{d_1}-\frac{1}{d_2}\right)+\frac{1}{2·\lambda_{из}}·\left(\frac{1}{d_2}-\frac{1}{d_{из}}\right)+\frac{1}{\alpha_2·d_{из}^2}} =$$ $$= \frac{\pi·(200-150)}{\frac{1}{10^4·0.050^2}+\frac{1}{2·45}·\left(\frac{1}{0.050}-\frac{1}{0.055}\right)+\frac{1}{2·0.01}·\left(\frac{1}{0.055}-\frac{1}{0.055+2·0.015}\right)+\frac{1}{10^4·(0.055+2·0.015)^2}} = 0.489.$$Находиться температуры стенок, °C:
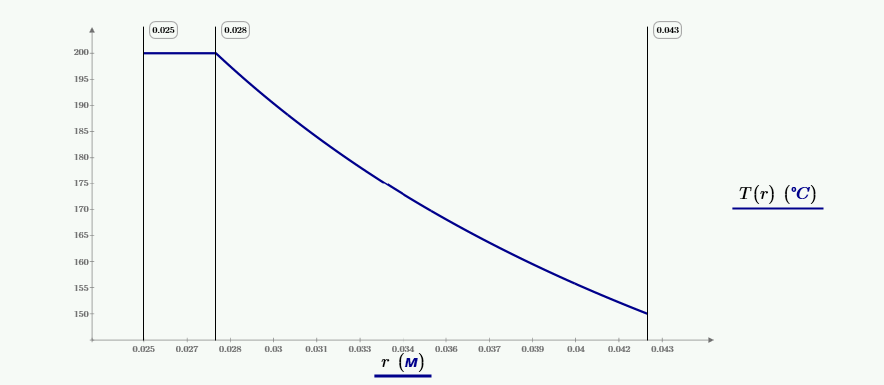
$$t_1 = -\frac{Q_{из}}{\alpha_1·\pi·d_1^2}+t_{ж1} = -\frac{0.489}{10^4·\pi·0.050^2}+200 = 200,$$ $$t_2 = \frac{Q_{из}}{\pi}\frac{1}{2·\lambda}·\left(\frac{1}{d_1}-\frac{1}{d_2}\right) = \frac{0.489}{\pi}\frac{1}{2·45}·\left(\frac{1}{0.050}-\frac{1}{0.055}\right) = 200.$$ $$t_{из} = \frac{Q_{из}}{\alpha_2·\pi·d_{из}^2}+t_{ж2} = -\frac{0.489}{10^4·\pi·(0.055+2·0.015)^2}+150 = 150.$$Изоляция целесообразна, т.к. критический диаметр равен, м:
$$d_{кр} = \frac{4·\lambda_{из}}{\alpha_2} = \frac{4·0.01}{10^4} = 4·10^{-6} < 0.055.$$Произошло уменьшение тепловых потерь примерно в 3500 раз.
$$\frac{Q}{Q_{из}} \approx 5600.$$

Создаем модель не изолированного шара
Создаем сетку

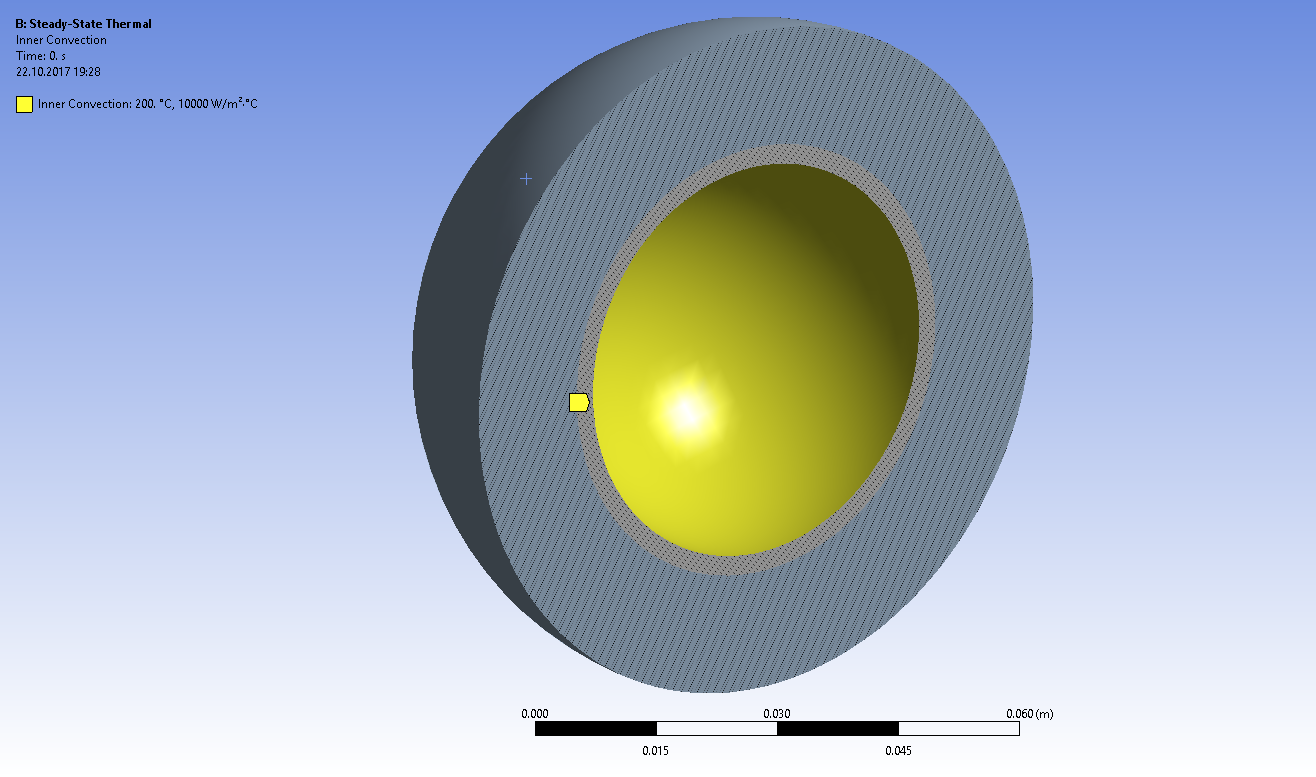
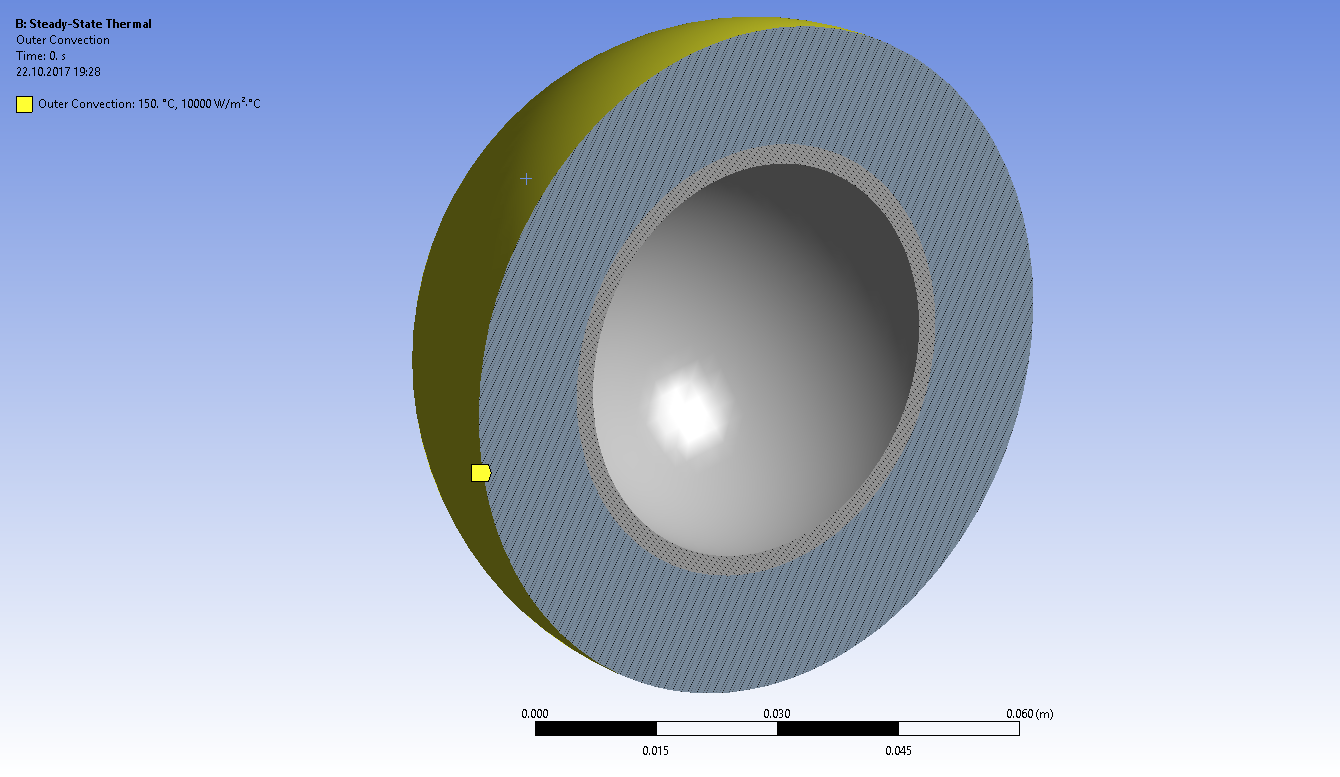
Задаем граничные условия конвективного теплообмена на внутренней и наружной поверхностях шара
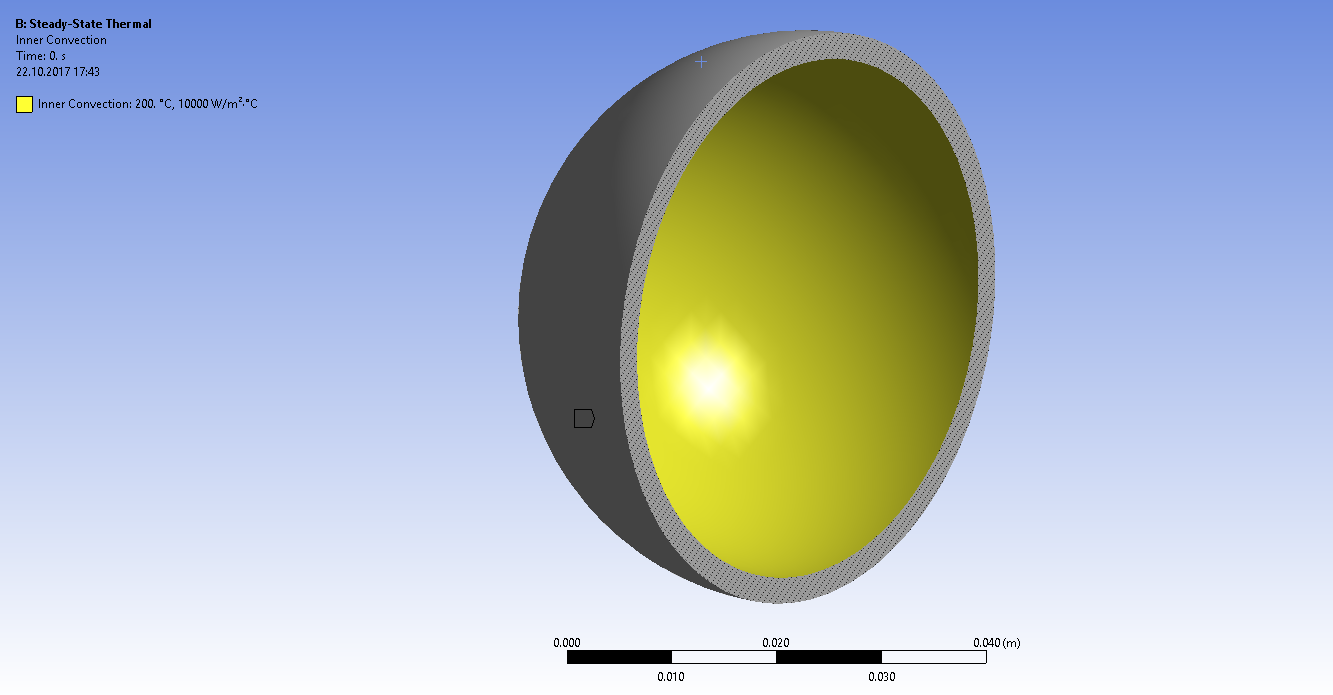
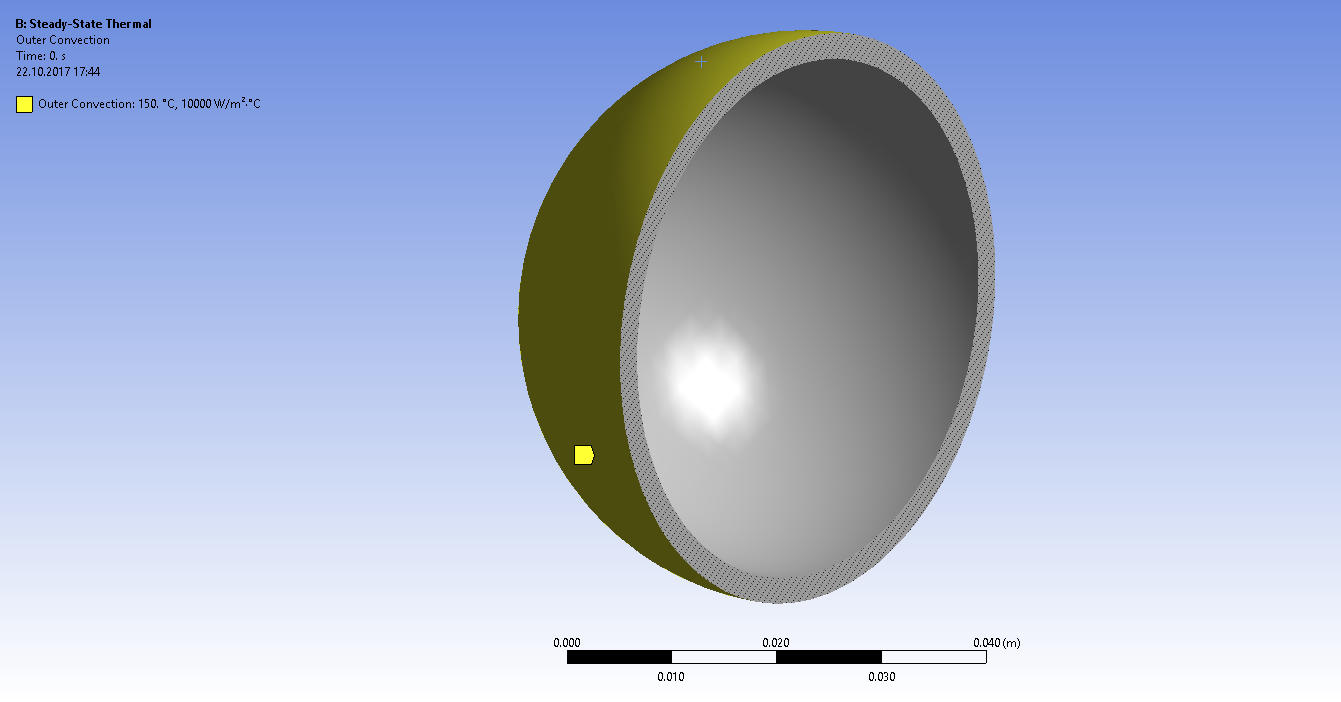
Получаем распределение температур по радиусу шара
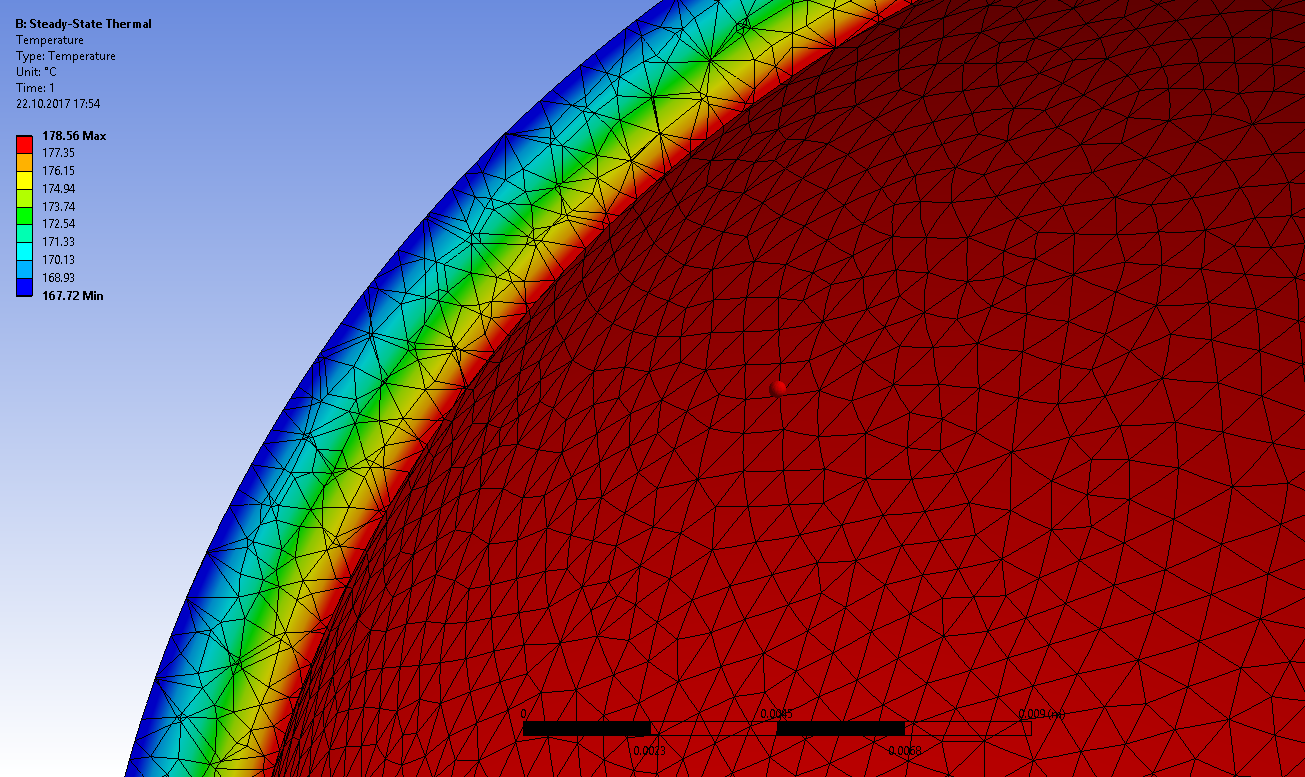
и тепловой поток через всю поверхность шара
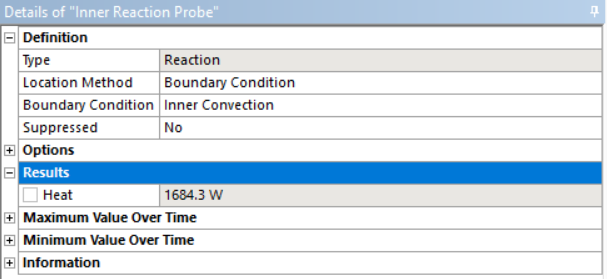
Создаем модель изолированного шара
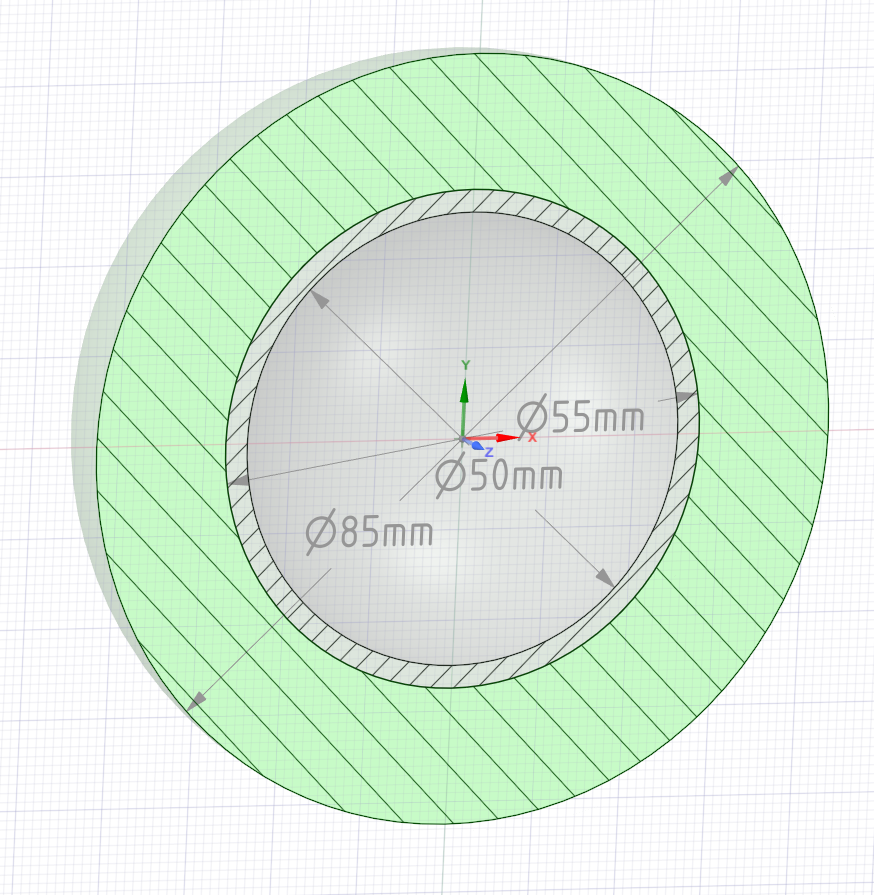
Создаем сетку

Задаем граничные условия конвективного теплообмена на внутренней поверхности шара и наружной поверхности изоляции
Получаем распределение температур по радиусу шара и изоляции

и тепловой поток через всю поверхность шара
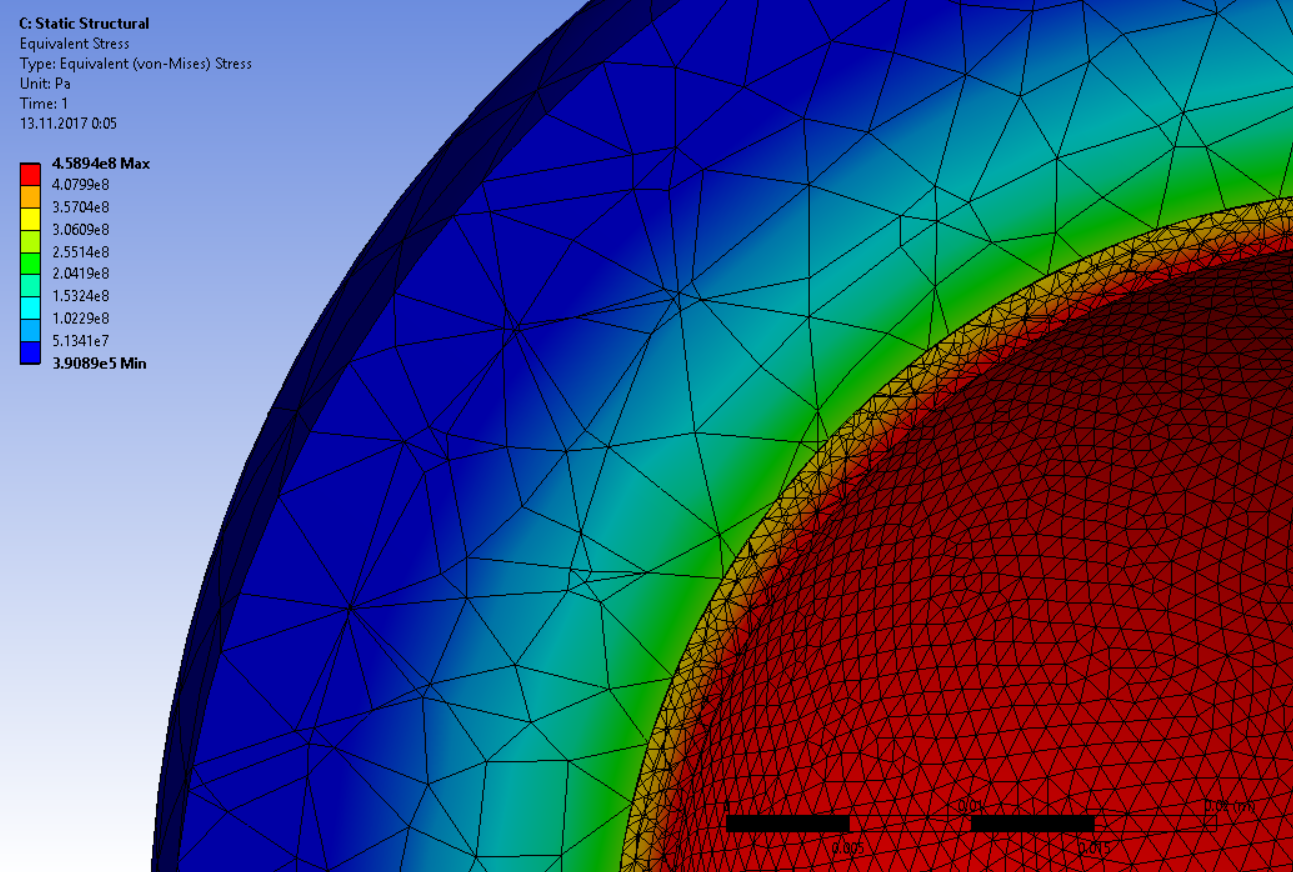
Получаем распределение деформаций внутри шара и изоляции

и распределение термических напряжений