Металлический слиток имеющий форму цилиндра диаметром и высотой равными $d = 350$ мм имел начальную температуру $t_0 = 25$ °C, а затем был положен в печь с температурой $t_ж = 1000$ °С. Коэффициент теплопроводности металла $\lambda = 10$ Вт/м·К, плотность $\rho = 9000$ кг/м3, теплоемкость $c_p = 360$ Дж/кг·К, коэффициент теплоотдачи на поверхности $\alpha = 25$ Вт/м2·К. Определить температуры в центре слитка, в срединах торцовых поверхностей и на их образующих через $\tau = 5$ минут после его загрузки в печь, количество теплоты, сообщенное слитку за это время.
Для оси z
Число Био:
$$Bi = \frac{\frac{a}{2·\lambda}}{\frac{1}{\alpha}} = \frac{\frac{0.35}{2·10}}{\frac{1}{25}} = 0.437.$$Числа подобия по таблице в зависимости от числа Био: $\mu_1=0.59$, $\mu_2=3.26$, $A_1=1.05$, $A_2=-0.07$
Число Фурье:
$$Fo = \frac{a·\tau}{\left(\frac{a}{2}\right)^2} = \frac{3.1·10^{-6}·3000}{\left(\frac{0.35}{2}\right)^2} = 0.302.$$Для расчета используется два члена ряда:
$$\theta(Z) = A_1·\cos{(\mu_1·Z)}·\exp{(-\mu_1^2·Fo)} + A_2·\cos{(\mu_2·Z)}·\exp{(-\mu_2^2·Fo)}.$$В центре пластины безразмерная координата равна $Z=0$, тогда безразмерная температура равна:
$$\theta(Z=0) = 1.05·\exp{(-0.59^2·0.302)} + (-0.07)·\exp{(-3.26^2·0.302)} = 0.944.$$На поверхности пластины безразмерная координата равна $Z=1$, тогда безразмерная температура равна:
$$\theta(Z=1) = 1.05·\cos{(0.59·1)}·\exp{(-0.59^2·0.302)} + (-0.07)·\cos{(3.26·1)}·\exp{(-3.26^2·0.302)} = 0.776.$$Для оси r
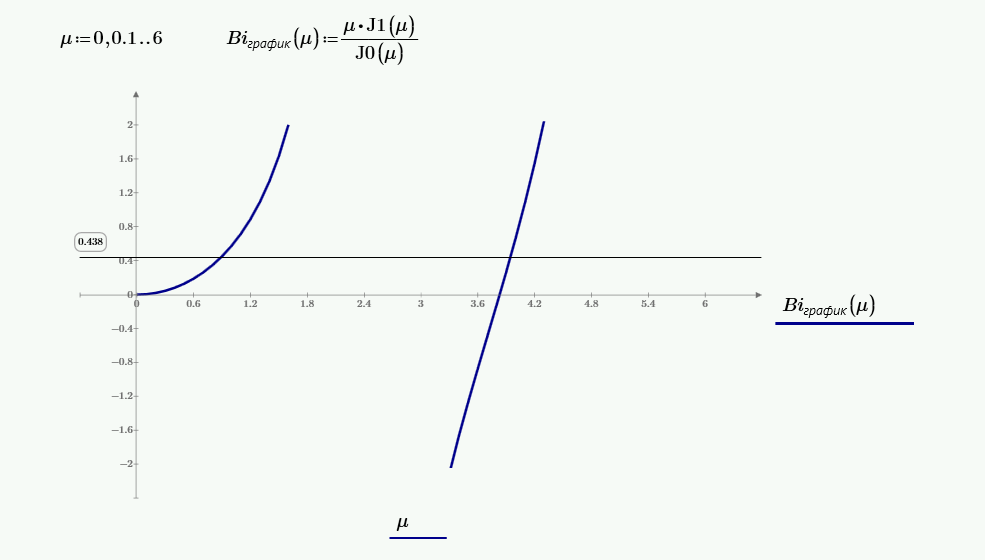
Число Био:
$$Bi = \frac{\frac{a}{2·\lambda}}{\frac{1}{\alpha}} = \frac{\frac{0.35}{2·10}}{\frac{1}{25}} = 0.437.$$Числа подобия по таблице в зависимости от числа Био: $\mu_1=0.85$, $\mu_2=3.93$, $A_1=1.09$, $A_2=-0.12$.
Число Фурье:
$$Fo = \frac{a·\tau}{\left(\frac{a}{2}\right)^2} = \frac{3.1·10^{-6}·3000}{\left(\frac{0.35}{2}\right)^2} = 0.302.$$Для расчета используется два члена ряда:
$$\theta(R) = A_1·J_0(\mu_1·R)·\exp{(-\mu_1^2·Fo)} + A_2·J_0(\mu_2·R)·\exp{(-\mu_2^2·Fo)}.$$В центре пластины безразмерная координата равна $R=0$, тогда безразмерная температура равна:
$$\theta(R=0) = 1.09·\exp{(-0.85^2·0.302)} + (-0.12)·\exp{(-3.93^2·0.302)} = 0.885.$$На поверхности пластины безразмерная координата равна $R=1$, тогда безразмерная температура равна:
$$\theta(R=1) = 1.09·J_0(0.85·1)·\exp{(-0.85^2·0.302)} + (-0.12)·J_0(3.93·1)·\exp{(-3.93^2·0.302)} = 0.723.$$Находим безразмерную температуру центра:
$$\theta_ц = \theta(Z=0)·\theta(R=0) = 0.944·0.885 = 0.835.$$Находим температуру центра, °C:
$$t_ц=\theta_ц·(t_0-t_ж)+t_ж = 0.835·(25-1000)+1000 = 185.$$Находим безразмерную температуру угла:
$$\theta_в = \theta(Z=1)·\theta(R=1) = 0.776·0.723 = 0.561.$$Находим температуру угла, °C:
$$t_в=\theta_в·(t_0-t_ж)+t_ж = 0.561·(25-1000)+1000 = 453.$$Находим безразмерную температуру середин граней:
$$\theta_R = \theta(Z=0)·\theta(R=1) = 0.944·0.723 = 0.683.$$ $$\theta_Z = \theta(Z=1)·\theta(R=0) = 0.776·0.885 = 0.687.$$Находим температуру середин граней, °C:
$$t_R=\theta_в·(t_0-t_ж)+t_ж = 0.683·(25-1000)+1000 = 330.$$ $$t_Z=\theta_в·(t_0-t_ж)+t_ж = 0.687·(25-1000)+1000 = 334.$$Средняя безразмерная температура в слитке:
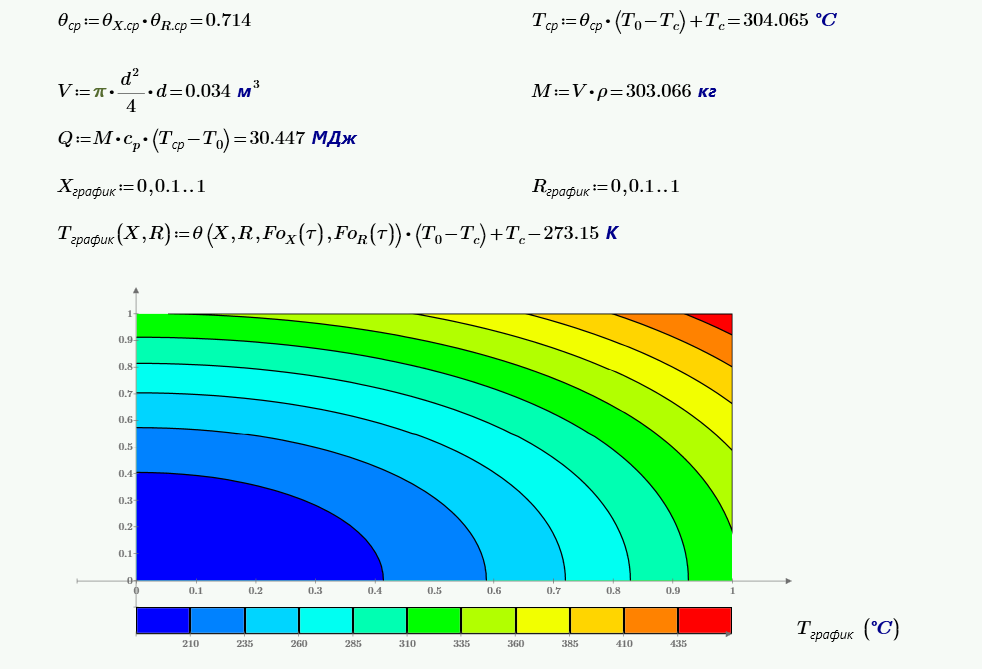
$$\overline{\theta} = \int_0^1\theta_Z\partial Z·2·\int_0^1\theta_R·R\partial R = 0.888·0.803 = 0.714.$$Средняя температура в слитке, °C:
$$\overline{t}=\overline{\theta}·(t_0-t_ж)+t_ж = 0.714·(25-1000)+1000 = 304.$$Количество теплоты, сообщенное слитку, МДж:
$$Q = 0.25·\pi·d^3·\rho·c_p·(\overline{t}-t_0) = 0.25·\pi·0.35^3·9000·360·(304-25) = 30.$$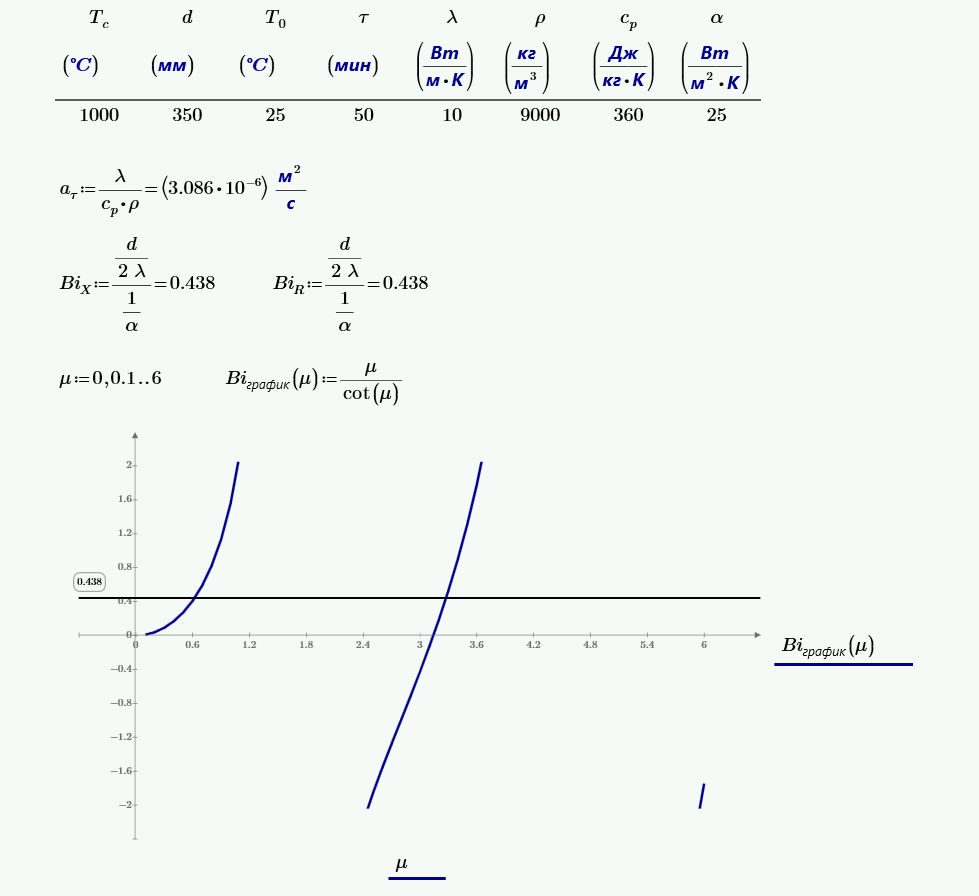



Создаем модель
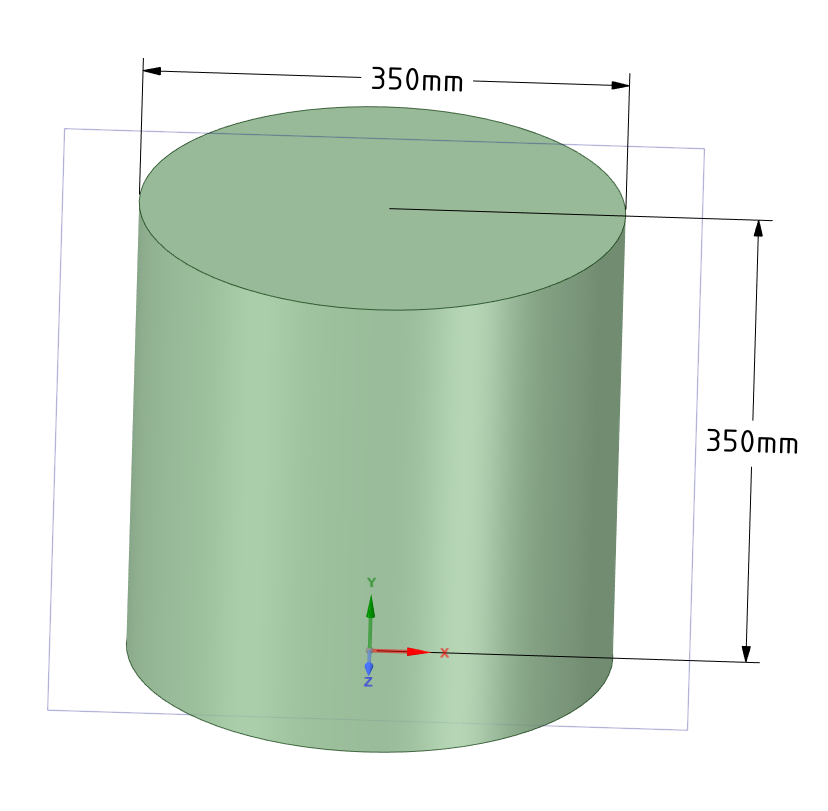
Создаем сетку

Задаем граничные условия конвективного теплообмена на поверхности

Получаем распределение температур по окончанию процесса

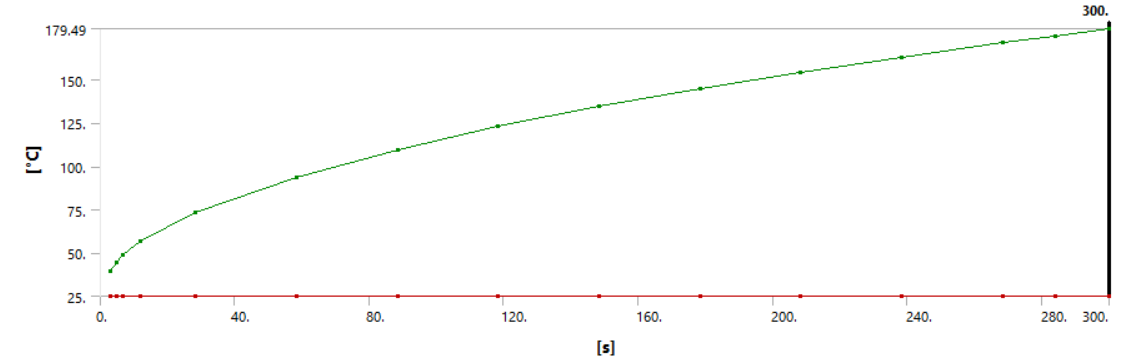
Получаем изменение максимальной и минимальной температур во времени
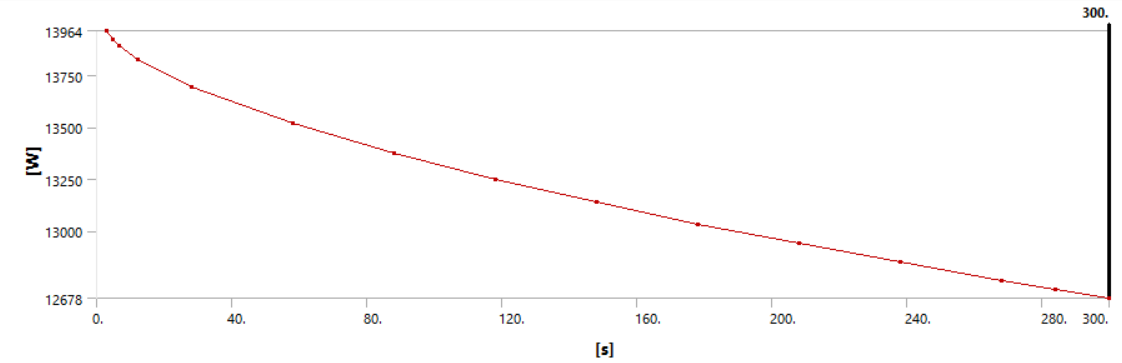
Получаем изменение теплового потока с поверхности во времени