Трубный пучок, выполненный из стальных труб внутренним диаметром $d_1 = 100$ мм и наружным $d_2 = 105$ мм, обдувается поперечным потоком воздуха со скоростью $\omega_г = 25$ м/с и температурой $t_г = 600$ °C. Внутри труб протекает вода со скоростью $\omega_в = 0.5$ м/с и средней температурой $t_в = 60$ °C. Продольный и поперечный шаги трубного пучка $S_1$ и $S_2$, при этом $S_1/d_2 = 4$ и $S_2/d_2 = 4$. Расположение труб шахматное. Определить средние коэффициенты теплоотдачи и линейные плотности теплового потока для первого и третьего рядов трубного пучка.
Свойства воды берем по таблице:
| $t$, °C | $\lambda$, Вт/м·К | $\nu$, м2/с | $Pr$ |
|---|---|---|---|
| $60$ | $0.659$ | $0.478·10^{-6}$ | $2.98$ |
Рассчитываем коэффициент теплоотдачи для воды внутри трубы, при условии его вынужденного движения. Для этого определяем число Рейнольдса:
$$Re = \frac{\omega_1·d_1}{\nu_1} = \frac{0.5·0.1}{0.478·10^{-6}} = 1.05·10^5 > 10^4$$режим течения турбулентный.
Число Нуссельта:
$$Nu = 0.021·Re^{0.8}·Pr^{0.43} = 0.021·(1.05·10^5)^{0.8}·2.98^{0.43} = 348.$$Обратите внимание! Для воды необходимо учитывать поправку Михеева $\left(\frac{Pr}{Pr_c}\right)^{0.25}$. Однако в данном примере расчет произведен без учета поправки Михеева, т.к. коэффициент теплоотдачи со стороны воды много больше, чем со стороны воздуха и температура стенки близка к температуре воды, т.е. $\left(\frac{Pr}{Pr_c}\right)^{0.25} \approx 1$.
Коэффициент теплоотдачи, Вт/м2·К:
$$\alpha_1 = \frac{Nu·\lambda}{d_1} = \frac{348·0.659}{0.1} = 2300.$$Свойства воздуха берем по таблице:
| $t$, °C | $\lambda$, Вт/м·К | $\nu$, м2/с | $Pr$ |
|---|---|---|---|
| $600$ | $0.0622$ | $96.9·10^{-6}$ | $0.7$ |
Рассчитываем коэффициент теплоотдачи для воздуха снаружи трубы, при условии его вынужденного движения в шахматном пучке труб. Для этого определяем число Рейнольдса:
$$Re = \frac{\omega_2·d_2}{\nu_2} = \frac{25·0.105}{96.9·10^{-6}} = 3.75·10^4.$$Число Нуссельта для третьего ряда труб для воздуха:
$$Nu = 0.41·Re^{0.6}·Pr^{0.33}·\left(\frac{S_1}{S_2}\right)^{\frac{1}{6}}·\varepsilon_i = 0.41·(3.75·10^4)^{0.6}·0.7^{0.33}·\left(1\right)^{\frac{1}{6}}·1 = 202.$$Коэффициент теплоотдачи для третьего ряда труб для воздуха, Вт/м2·К:
$$\alpha_2 = \frac{Nu·\lambda}{d_2} = \frac{202·0.0622}{0.105} = 120.$$Теплота, передаваемая через стенку трубы, для третьего ряда труб, Вт/м:
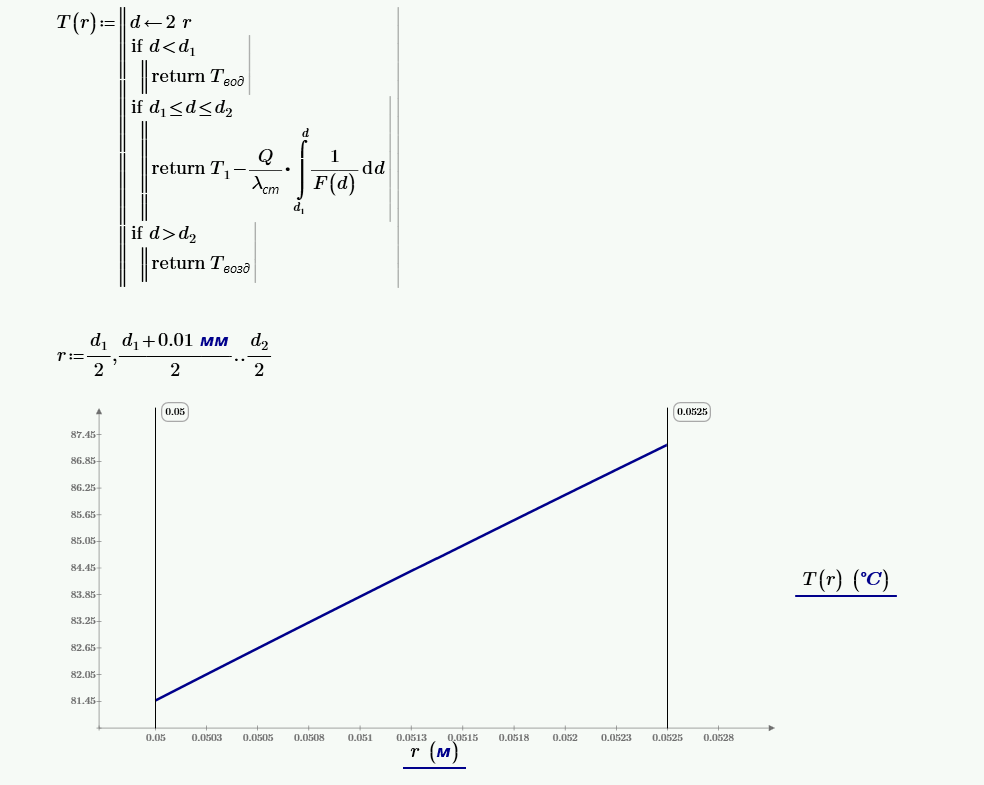
$$q_l = \frac{\pi·(t_2-t_1)}{\frac{1}{\alpha_1·d_1}+\frac{1}{2·\lambda}·\ln{\left(\frac{d_2}{d_1}\right)}+\frac{1}{\alpha_2·d_2}} = $$ $$= \frac{\pi·(600-60)}{\frac{1}{2300·0.1}+\frac{1}{2·45}·\ln{\left(\frac{0.105}{0.1}\right)}+\frac{1}{120·0.105}} = 2·10^4.$$Температура стенки со стороны воды, °С:
$$t_{c1} = \frac{q_l}{\alpha_1·\pi·d_1} + t_1 = \frac{2·10^4}{2300·\pi·0.1} + 60 = 87.7.$$Число Нуссельта для первого ряда труб для воздуха:
$$Nu = 0.41·Re^{0.6}·Pr^{0.33}·\left(\frac{S_1}{S_2}\right)^{\frac{1}{6}}·\varepsilon_i = 0.41·(3.75·10^4)^{0.6}·0.7^{0.33}·\left(1\right)^{\frac{1}{6}}·0.6 = 121.$$Коэффициент теплоотдачи для первого ряда труб для воздуха, Вт/м2·К:
$$\alpha_2 = \frac{Nu·\lambda}{d_2} = \frac{121·0.0622}{0.105} = 72.$$Теплота, передаваемая через стенку трубы, для первого ряда труб:
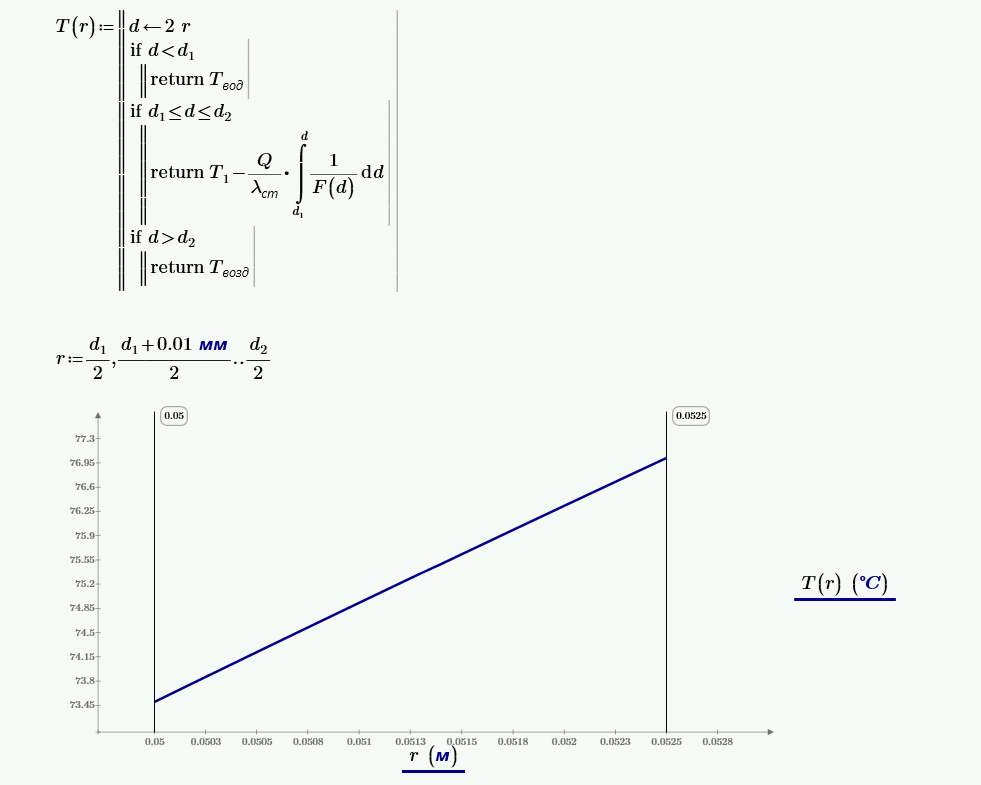
$$q_l = \frac{\pi·(t_2-t_1)}{\frac{1}{\alpha_1·d_1}+\frac{1}{2·\lambda}·\ln{\left(\frac{d_2}{d_1}\right)}+\frac{1}{\alpha_2·d_2}} = $$ $$= \frac{\pi·(600-60)}{\frac{1}{2300·0.1}+\frac{1}{2·45}·\ln{\left(\frac{0.105}{0.1}\right)}+\frac{1}{72·0.105}} = 1.2·10^4.$$Температура стенки со стороны воды, °С:
$$t_{c1} = \frac{q_l}{\alpha_1·\pi·d_1} + t_1 = \frac{1.2·10^4}{2300·\pi·0.1} + 60 = 76.6.$$