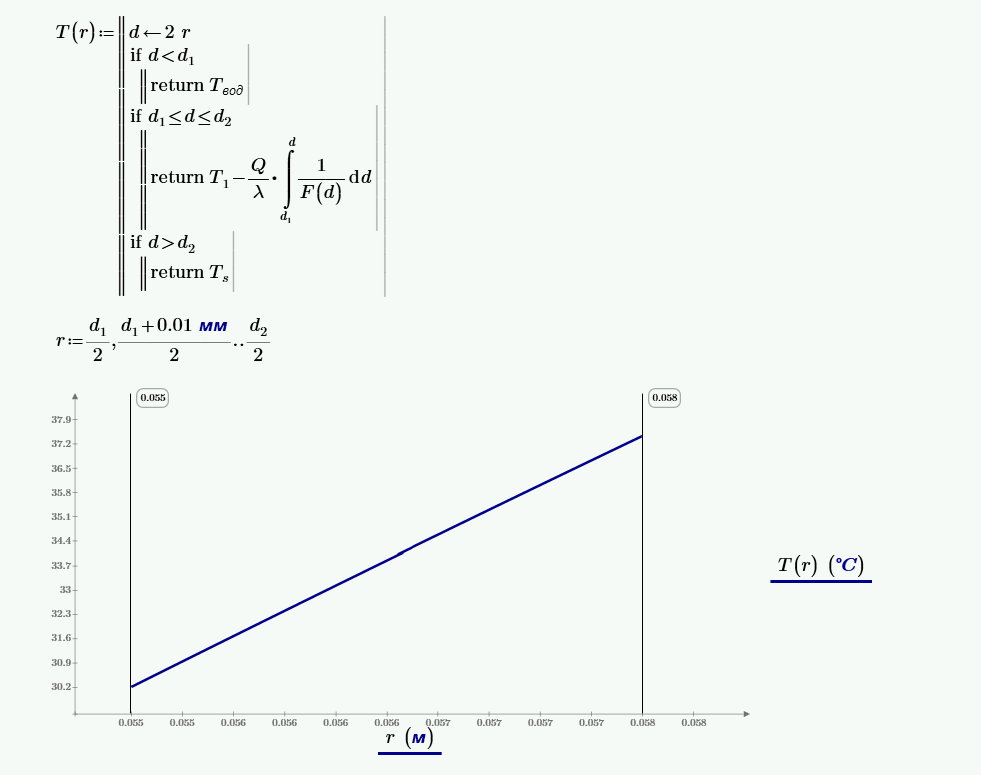
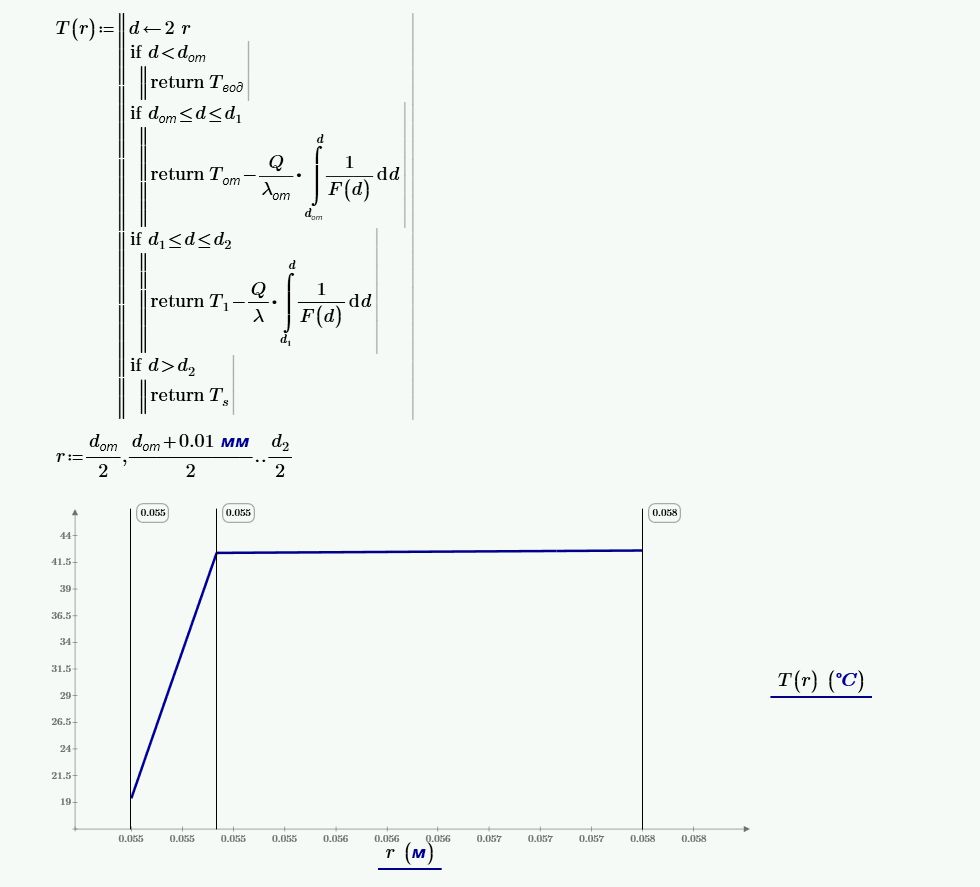
По трубе внутренним диаметром $d_1 = 110$ мм и наружным $d_2 = 115$ мм протекает вода со скоростью $\omega = 1.4$ м/с и средней температурой $t_ж = 19$ °C. С наружной стороны на поверхности трубы конденсируется сухой насыщенный пар при давлении $P = 8.5$ кПа. Коэффициент теплопроводности материала трубы $\lambda = 30$ Вт/м·К. Определить массу конденсата, которая образуется на каждом погонном метре трубы за 1 секунду, и массу конденсата при образовании на внутренней поверхности отложений толщиной $\delta = 0.5$ мм с коэффициентом теплопроводности $\lambda_{от} = 0.06$. Труба расположена горизонтально.
Решение:
Свойства воды берем по таблице:| $P$, бар | $t$, °C | $\lambda$, Вт/м·К | $\nu$, м2/с | $Pr$ |
|---|---|---|---|---|
| $1$ | $19$ | $0.599$ | $1.006·10^{-6}$ | $7.02$ |
| $0.085$ | $43$ | $0.635$ | $0.659·10^{-6}$ | $4.31$ |
Рассчитываем коэффициент теплоотдачи для воды внутри трубы, при условии его вынужденного движения. Для этого определяем число Рейнольдса:
$$Re = \frac{\omega_1·d_1}{\nu_1} = \frac{1.4·0.11}{1.005·10^{-6}} = 1.53·10^5 > 10^4$$режим течения турбулентный.
Рассчитываем число Нуссельта, принимая температуру стенки равную $t_c = 30$ °С:
$$Nu = 0.021·Re^{0.8}·Pr^{0.43}·\left(\frac{Pr}{Pr_c}\right)^{0.25} = 0.021·(1.53·10^5)^{0.8}·7.02^{0.43}·\left(\frac{7.02}{5.42}\right)^{0.25} = 727.$$Коэффициент теплоотдачи, Вт/м2·К:
$$\alpha_1 = \frac{Nu·\lambda}{d_1} = \frac{727·0.599}{0.11} = 3965.$$Рассчитываем коэффициент теплоотдачи для конденсации на горизонтальной трубе приняв температуру стенки равную $t_c = 30$ °С:
$$\alpha_2 = 0.728·\sqrt[4]{\frac{r·\rho_п·(\rho_ж-\rho_п)·g·\lambda_п^3}{\mu_п·\Delta t·d}} = 0.728·\sqrt[4]{\frac{2.25·10^6·0.06·(1000-0.06)·g·0.635^3}{0.659·10^{-6}·0.06·(43-30)·0.115}} = 6244.$$Теплота, передаваемая через стенку трубы, Вт/м:
$$q_l = \frac{\pi·(t_2-t_1)}{\frac{1}{\alpha_1·d_1}+\frac{1}{2·\lambda}·\ln{\left(\frac{d_2}{d_1}\right)}+\frac{1}{\alpha_2·d_2}} = $$ $$= \frac{\pi·(43-19)}{\frac{1}{3965·0.11}+\frac{1}{2·45}·\ln{\left(\frac{0.115}{0.1}\right)}+\frac{1}{6244·0.115}} = 1.68·10^4.$$Проверяем температуру стенки с внутренней стороны по уравнению Ньютона-Рихмана, °C:
$$t_c1 = t_1 + \frac{q_l}{\alpha_1·\pi·d_1} = 19 + \frac{1.68·10^4}{3965·\pi·0.11} = 31.$$Проверяем температуру стенки с внешней стороны по уравнению Ньютона-Рихмана, °C:
$$t_c2 = t_2 - \frac{q_l}{\alpha_2·\pi·d_2} = 43 + \frac{1.68·10^4}{6244·\pi·0.115} = 35.$$Разница между принятыми температурами стенки и найденными в результате расчета лежит в пределах погрешности.
Масса конденсата находиться по формуле, г/с:
$$m = \frac{q_l}{r} = \frac{1.68·10^4}{2.25·10^6} = 7.5.$$Аналогично рассчитываем для отложений.
Рассчитываем коэффициент теплоотдачи для воды внутри трубы, при условии его вынужденного движения. Для этого определяем число Рейнольдса:
$$Re = \frac{\omega_1·d_{от}}{\nu_1} = \frac{1.4·(0.11-2·0.0005)}{1.005·10^{-6}} = 1.53·10^5 > 10^4$$режим течения турбулентный.
Рассчитываем число Нуссельта, принимая температуру стенки равную $t_c = 20$ °С:
$$Nu = 0.021·Re^{0.8}·Pr^{0.43}·\left(\frac{Pr}{Pr_c}\right)^{0.25} = 0.021·(1.53·10^5)^{0.8}·7.02^{0.43}·\left(\frac{7.02}{7.02}\right)^{0.25} = 676.$$Коэффициент теплоотдачи, Вт/м2·К:
$$\alpha_1 = \frac{Nu·\lambda}{d_{от}} = \frac{676·0.599}{(0.11-2·0.0005)} = 3725.$$Рассчитываем коэффициент теплоотдачи для конденсации на горизонтальной трубе приняв температуру стенки равную $t_c = 42$ °С:
$$\alpha_2 = 0.728·\sqrt[4]{\frac{r·\rho_п·(\rho_ж-\rho_п)·g·\lambda_п^3}{\mu_п·\Delta t·d}} = 0.728·\sqrt[4]{\frac{2.25·10^6·0.06·(1000-0.06)·g·0.635^3}{0.659·10^{-6}·0.06·(43-42)·0.115}} = 1.29·10^4.$$Теплота, передаваемая через стенку трубы, Вт/м:
$$q_l = \frac{\pi·(t_2-t_1)}{\frac{1}{\alpha_1·d_{от}}+\frac{1}{2·\lambda_{от}}·\ln{\left(\frac{d_1}{d_{от}}\right)}+\frac{1}{2·\lambda}·\ln{\left(\frac{d_2}{d_1}\right)}+\frac{1}{\alpha_2·d_2}} = $$ $$= \frac{\pi·(43-19)}{\frac{1}{3725·(0.11-2·0.0005)}+\frac{1}{2·0.06}·\ln{\left(\frac{0.11}{0.11-2·0.0005}\right)}+\frac{1}{2·45}·\ln{\left(\frac{0.115}{0.11}\right)}+\frac{1}{1.29·10^4·0.115}} = 930.$$Проверяем температуру стенки с внутренней стороны по уравнению Ньютона-Рихмана, °C:
$$t_c1 = t_1 + \frac{q_l}{\alpha_1·\pi·d_1} = 19 + \frac{930}{3725·\pi·(0.11-2·0.0005)} = 20.$$Проверяем температуру стенки с внешней стороны по уравнению Ньютона-Рихмана, °C:
$$t_c2 = t_2 - \frac{q_l}{\alpha_2·\pi·d_2} = 43 + \frac{930}{1.29·10^4·\pi·0.115} = 42.$$Разница между принятыми температурами стенки и найденными в результате расчета лежит в пределах погрешности.
Масса конденсата находиться по формуле, г/с:
$$m = \frac{q_l}{r} = \frac{930}{2.25·10^6} = 0.41.$$