Определить толщину тепловой изоляции, которую нужно наложить на стену толщиной $\delta = 150$ мм, при условии, что температура поверхности изоляции не превышает $t_{из} = 45$ °С. Коэффициент теплопроводности материала $\lambda = 20$ Вт/м·К. Коэффициент теплоотдачи от жидкости к внутренней поверхности $\alpha_1 = 3000$ Вт/м2·К, к наружной поверхности $\alpha_2 = 17$ Вт/м2·К, температура жидкости внутри $t_{ж1} = 130$ °C, снаружи $t_{ж2} = 25$ °C. Материал изоляции имеет коэффициент теплопроводности равный $\lambda_{из} = 0.2$ Вт/м·К. Перед выполнением расчета оценить целесообразность тепловой изоляции.
Наложение тепловой изоляции целесообразно.
Обратите внимание! Плоская тепловая изоляция всегда целесообразна, так как ее площадь поверхности не меняется по сечению, однако для циллиндрической или шаровой поверхности такая проверка необходима.
Записывается система уравнений:
$$q = \alpha_1·(t_{ж1}-t_1);$$ $$q = \frac{\lambda}{\delta}·(t_1-t_2);$$ $$q = \frac{\lambda_{из}}{\delta_{из}}(t_2-t_{из});$$ $$q = \alpha_2·(t_{из}-t_{ж2}).$$Обратите внимание! Вид уравнений зависит от геометрии тела и определяется общими уравнениями Фурье $Q=-\lambda·\mathrm{grad}(T)·F$ и Ньютона-Рихмана $Q = \alpha·\Delta T·F$.
После суммирования получим тепловой поток равный:
$$q = \frac{t_{ж1}-t_{из}}{\frac{1}{\alpha_1}+\frac{\delta}{\lambda}+\frac{\delta_{из}}{\lambda_{из}}} = \alpha_2·(t_{из}-t_{ж2})$$или
$$\frac{130-45}{\frac{1}{3000}+\frac{0.150}{20}+\frac{\delta_{из}}{0.2}} = 17·(45-25)$$Решая уравнение находим толщину изоляции $\delta_{из} = 48.5·10^{-3}$ м.:

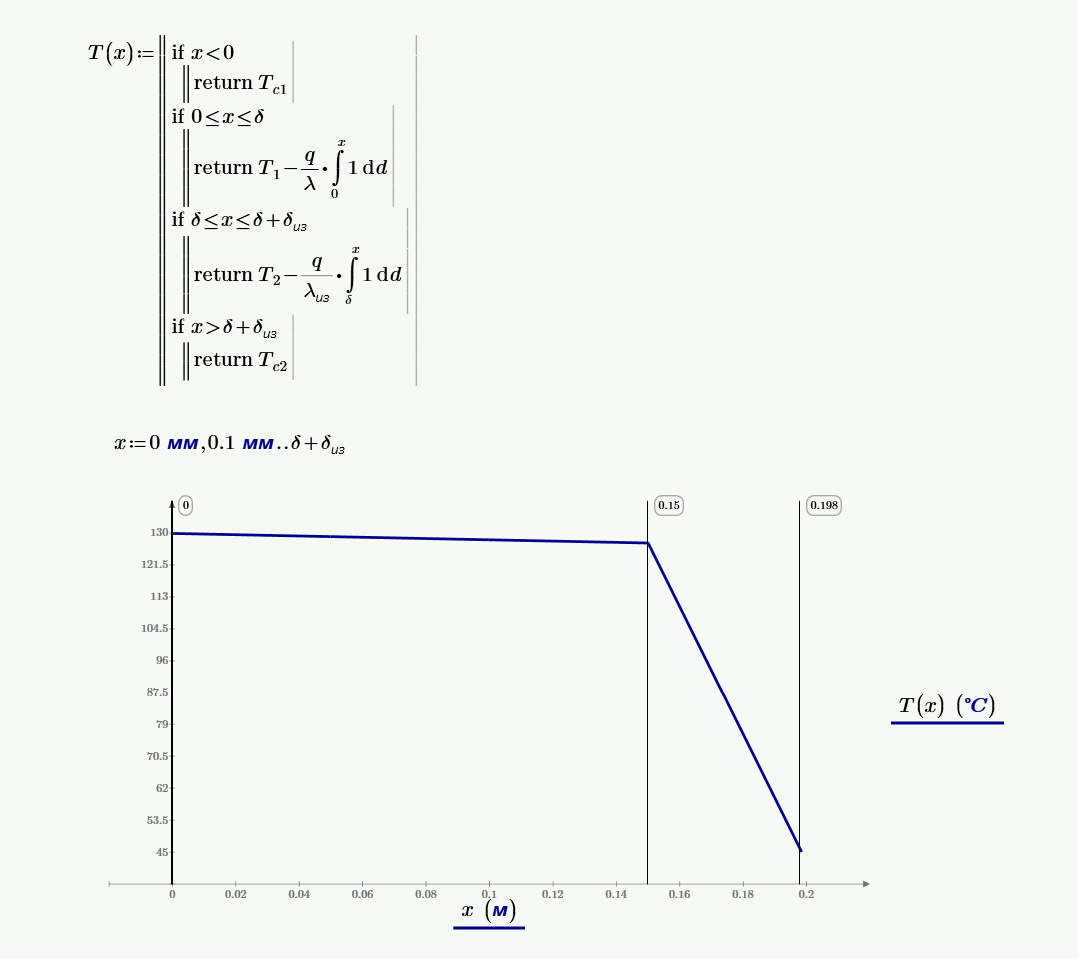
Создаем модель для проверки нашего решения
Создаем сетку

Задаем граничные условия идеальной изоляции для условий симметричности задачи, а также условия конвективного теплообмена с обоих сторон плоской стенки
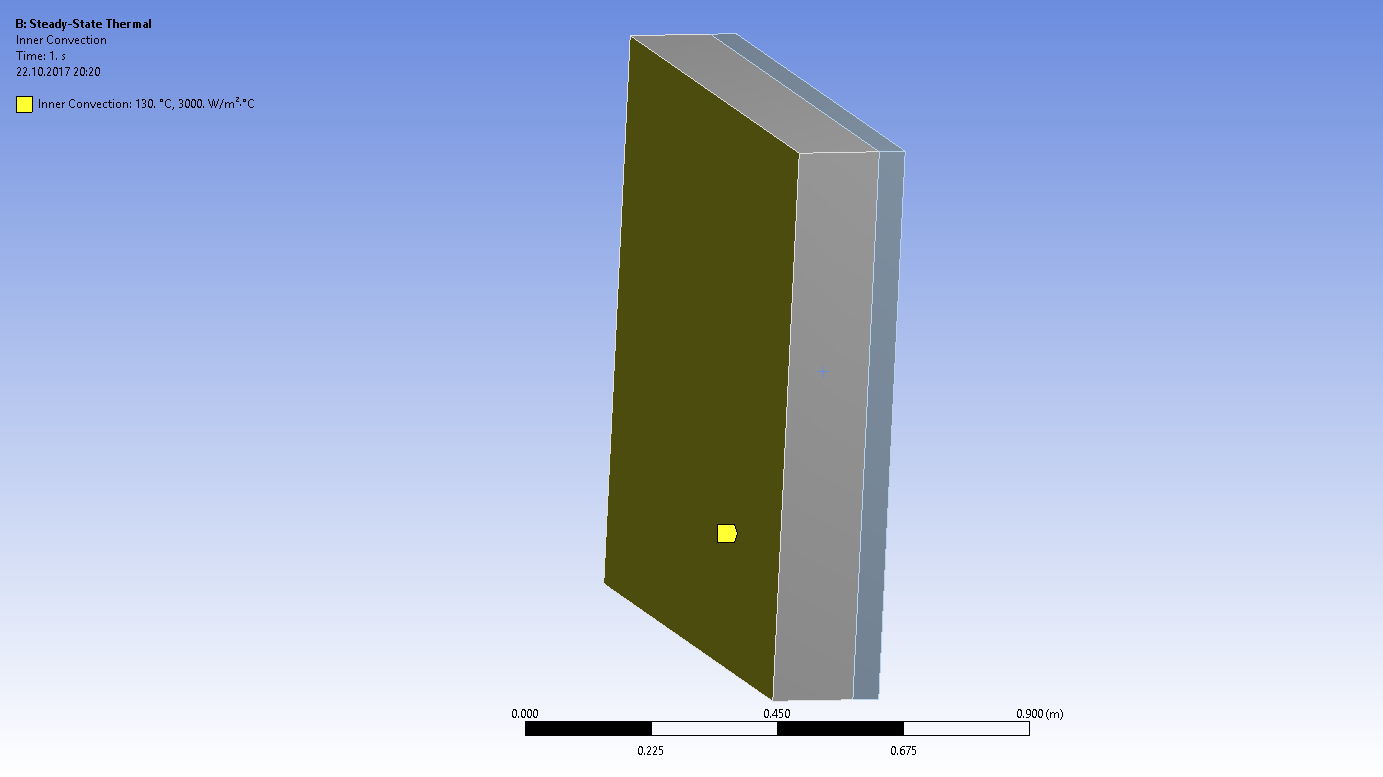
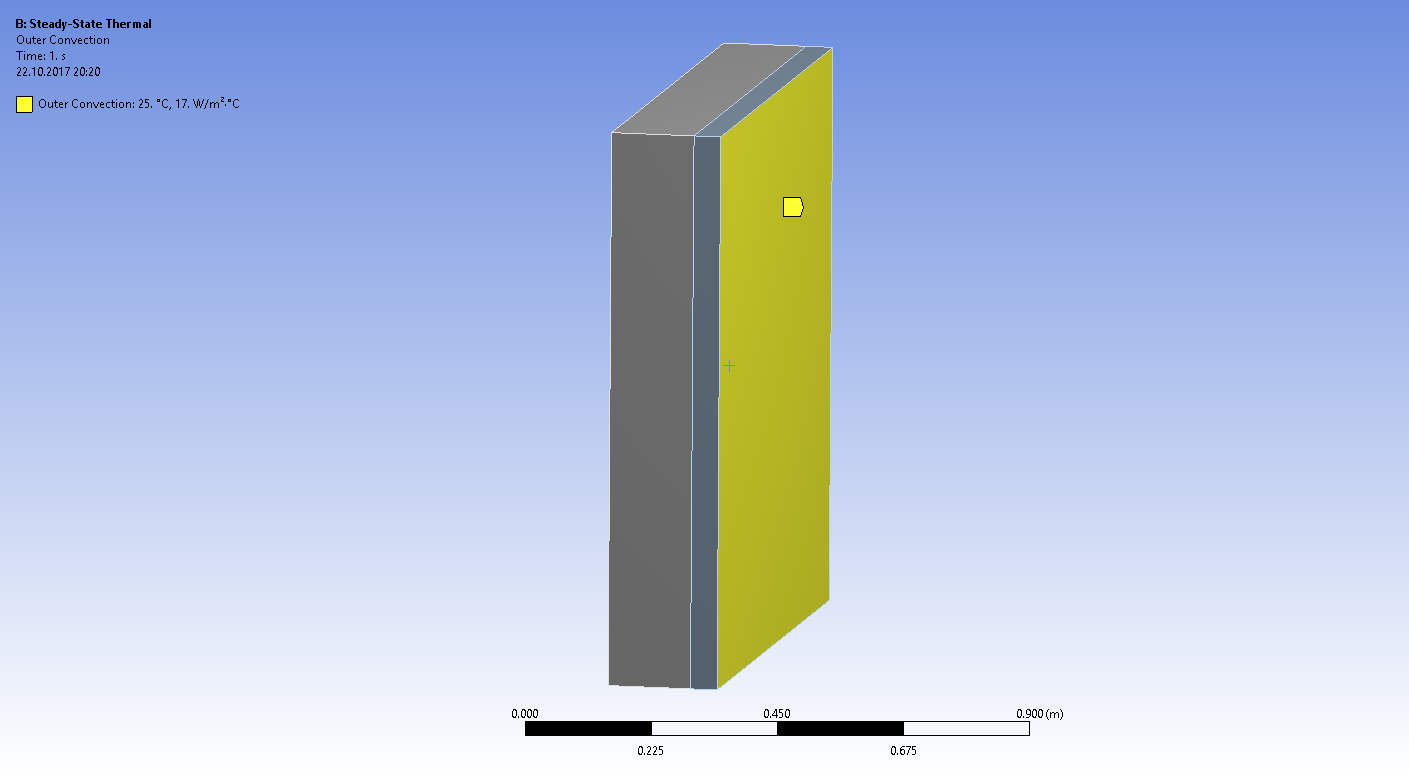
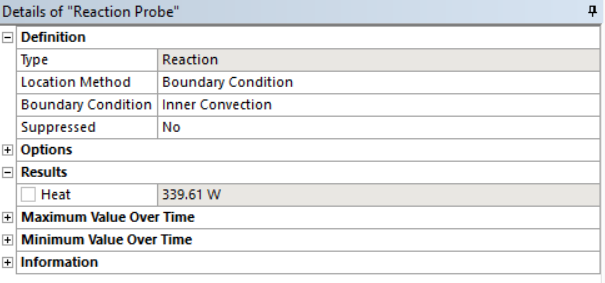
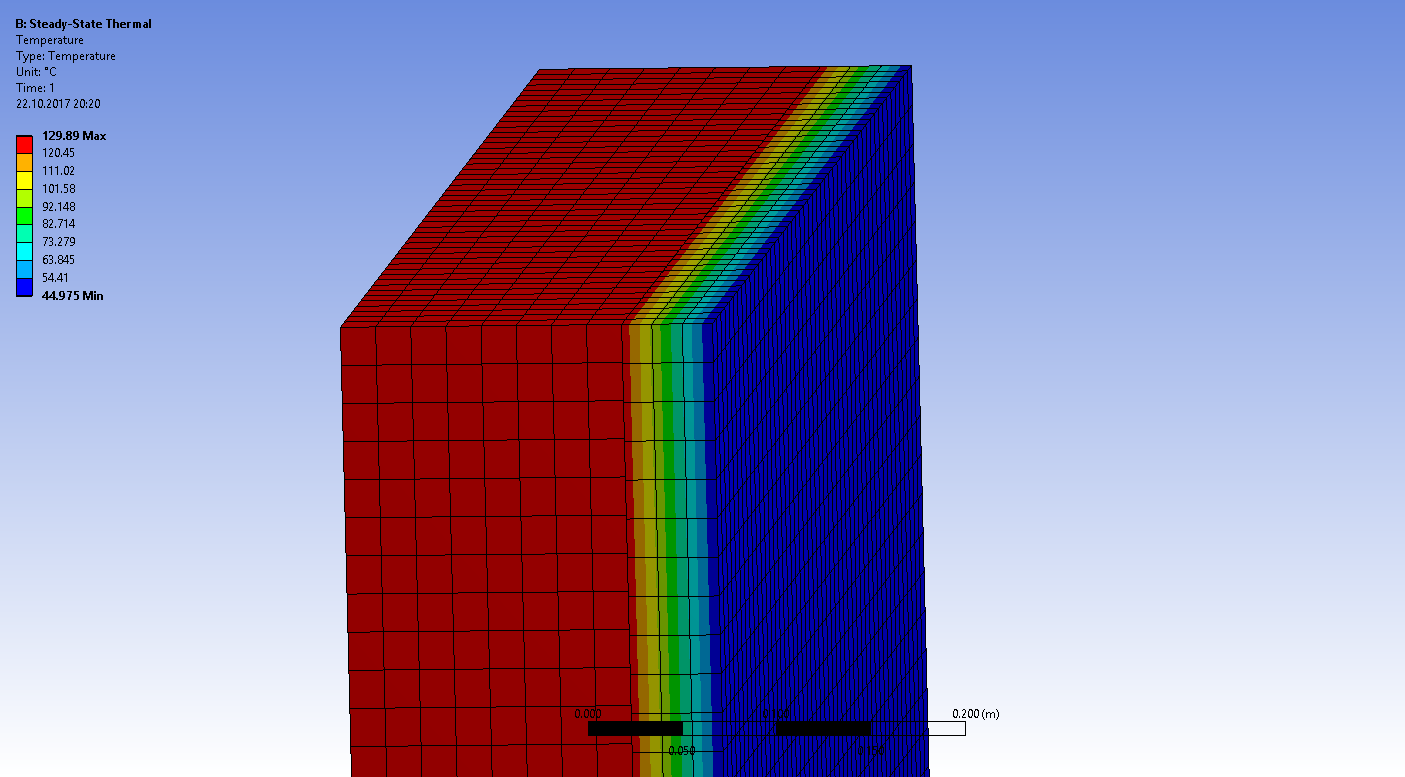
Получаем распределение температур, из которого видно, что температура поверхности изоляции не превышает 45°С - значит толщина изоляции выбрана верно
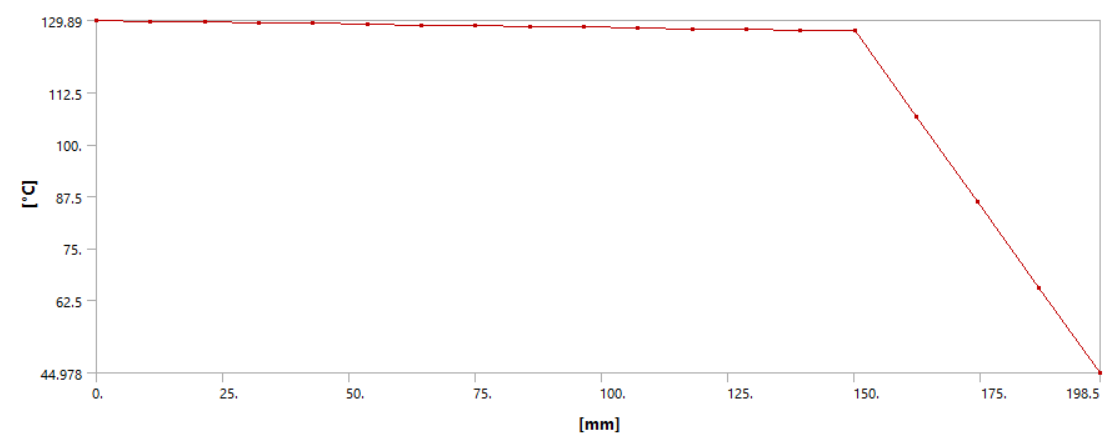
Получаем удельный тепловой поток через данныю стену