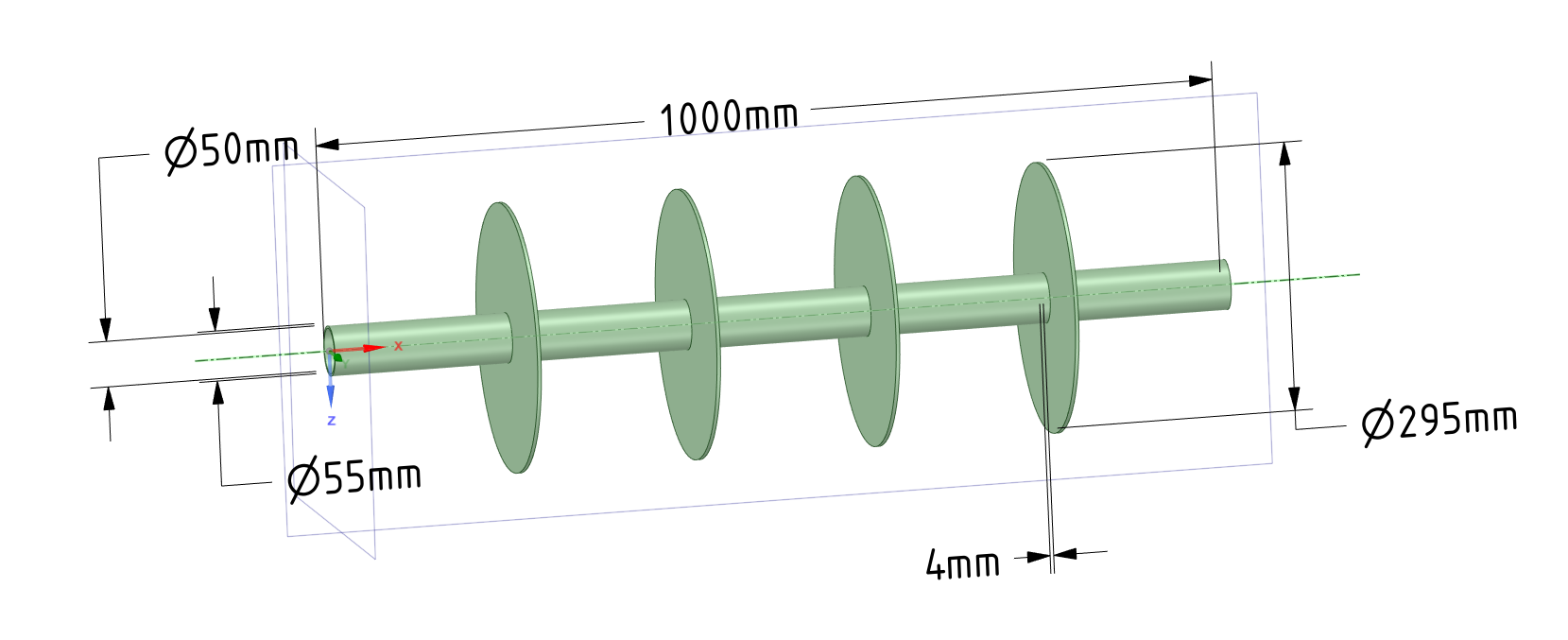
Определить потери теплоты с каждого погонного метра трубопровода, внутренним диаметром $d_1 = 50$ мм и наружным $d_2 = 55$ мм, и температуры на конце ребер. Коэффициент теплопроводности материала $\lambda = 45$ Вт/м·К. Коэффициент теплоотдачи от жидкости к внутренней поверхности $\alpha_1 = 10^4$ Вт/м2·К, к наружной поверхности $\alpha_2 = 100$ Вт/м2·К, температура жидкости внутри $t_{ж1} = 100$ °C, снаружи $t_{ж2} = 150$ °C. Количество ребер $n = 4$, высота ребра $h = 120$ мм, толщина $\delta_p = 4$ мм. Оценить эффективность оребрения.
Рассчитываем площадь внутри трубы, м2:
$$F_1 = \pi·d_1·l = \pi·0.050·1 = 0.157.$$Коэффициент оребрения:
$$\psi = \frac{I_1(m·r_{ребра})·K_1(m·r_2)-I_1(m·r_2)·K_1(m·r_{ребра})}{I_0(m·r_2)·K_1(m·r_{ребра})+I_1(m·r_{ребра})·K_0(m·r_2)} = $$ $$= \frac{I_1(33.8·\left(\frac{0.055}{2}+0.12\right))·K_1(33.8·\left(\frac{0.055}{2}\right))-I_1(33.8·\left(\frac{0.055}{2}\right))·K_1(33.8·\left(\frac{0.055}{2}+0.12\right))}{I_0(33.8·\left(\frac{0.055}{2}\right))·K_0(33.8·\left(\frac{0.055}{2}+0.12\right))+I_0(33.8·\left(\frac{0.055}{2}+0.12\right))·K_0(33.8·\left(\frac{0.055}{2}\right))} = 1.457,$$где коэффициент m, 1/м:
$$m = \sqrt{\frac{\alpha_2·2·(h+\delta_p)}{\lambda·(h·\delta_p)}} = \sqrt{\frac{100·2·(0.12+0.004)}{45·(0.12·0.004)}} = 33.8.$$Коэффициент оребрения для определения температуры:
$$\psi_{ребра} = \frac{I_0(m·r_{ребра})·K_1(m·r_{ребра})+I_1(m·r_{ребра})·K_0(m·r_{ребра})}{I_0(m·r_2)·K_1(m·r_{ребра})+I_1(m·r_{ребра})·K_0(m·r_2)} = $$ $$= \frac{I_0(33.8·\left(\frac{0.055}{2}+0.12\right))·K_1(33.8·\left(\frac{0.055}{2}+0.12\right))+I_1(33.8·\left(\frac{0.055}{2}+0.12\right))·K_0(33.8·\left(\frac{0.055}{2}+0.12\right))}{I_0(33.8·\left(\frac{0.055}{2}\right))·K_1(33.8·\left(\frac{0.055}{2}+0.12\right))+I_1(33.8·\left(\frac{0.055}{2}+0.12\right))·K_0(33.8·\left(\frac{0.055}{2}\right))} = 0.018,$$Обратите внимание! Вид уравнений зависит от геометрии ребер.
Записывается система уравнений:
$$Q = \alpha_1·(t_{ж1}-t_1)·F_1;$$ $$Q = \frac{2·\pi·\lambda·l·(t_1-t_2)}{\ln{\frac{d_2}{d_1}}};$$ $$Q = (\alpha_2·(d_2·(l-n·\delta_p))+2·\pi·r_2·\lambda·\delta_p·m·\psi·n + \alpha_2·\psi_{ребра}·\pi·d_2·n·\delta_p)·(t_2-t_{ж2}).$$Обратите внимание! Вид уравнений зависит от геометрии тела и определяется общими уравнениями Фурье $Q=-\lambda·\mathrm{grad}(T)·F$ и Ньютона-Рихмана $Q = \alpha·\Delta T·F$.
После суммирования получим тепловой поток равный, Вт:
$$Q = \frac{t_{ж1}-t_{ж2}}{\frac{1}{\alpha_1·F_1}+\frac{1}{2·\pi·\lambda}·\ln\left(\frac{d_2}{d_1}\right)+\frac{1}{\alpha_2·(d_2·(l-n·\delta_p))+2·\pi·r_2·\lambda·\delta_p·m·\psi·n + \alpha_2·\psi_{ребра}·\pi·d_2·n·\delta_p}} = $$ $$ = \frac{100-150}{\frac{1}{10^4·0.157}+\frac{1}{2·\pi·45}·\ln\left(\frac{0.055}{0.050}\right)+\frac{1}{100·(0.055·(1-4·0.004))+2·\pi·0.0275·45·0.004·33.8·1.457·4 + 100·0.018·\pi·0.055·4·0.004}} = -1123.$$Обратите внимание! Знак минус указывает на направление теплового потока.
Находим температуру на внешней стороне трубы, °С:
$$t_2 = \frac{Q}{\alpha_2·(d_2·(l-n·\delta_p))+2·\pi·r_2·\lambda·\delta_p·m·\psi·n + \alpha_2·\psi_{ребра}·\pi·d_2·n·\delta_p} - t_{ж2} = $$ $$ = \frac{1400}{100·(0.055·(1-4·0.004))+2·\pi·0.0275·45·0.004·33.8·1.457·4 + 100·0.018·\pi·0.055·4·0.004} - 150 = 101.5;$$Температура на конце ребер, °C:
$$t_p = (t_2 - t_{ж2})·\psi_{ребра} + t_{ж2} = (101.5-150)·0.018 + 150 = 149.1.$$Записывается система уравнений без ребер:
$$Q = \alpha_1·(t_{ж1}-t_1)·F_1;$$ $$Q = \frac{2·\pi·\lambda·l·(t_1-t_2)}{\ln{\frac{d_2}{d_1}}};$$ $$Q = \alpha_2·(t_2-t_{ж2})·F_2.$$После суммирования получим тепловой поток равный, Вт:
$$Q = \frac{t_{ж1}-t_{ж2}}{\frac{1}{\alpha_1·F_1}+\frac{1}{2·\pi·\lambda}·\ln\left(\frac{d_2}{d_1}\right)+\frac{1}{\alpha_2·F_2}} = \frac{100-150}{\frac{1}{10^4·0.157}+\frac{1}{2·\pi·45}·\ln\left(\frac{0.055}{0.050}\right)+\frac{1}{100·(0.055·\pi·1)}} = -845.$$Можно сделать вывод, что в данном случае применение оребрения увеличивает теплопередачу примерно в 1.33 раза.



Создаем модель оребренной трубы
Создаем сетку

Задаем граничные условия конвективного теплообмена внутри трубы и снаружи
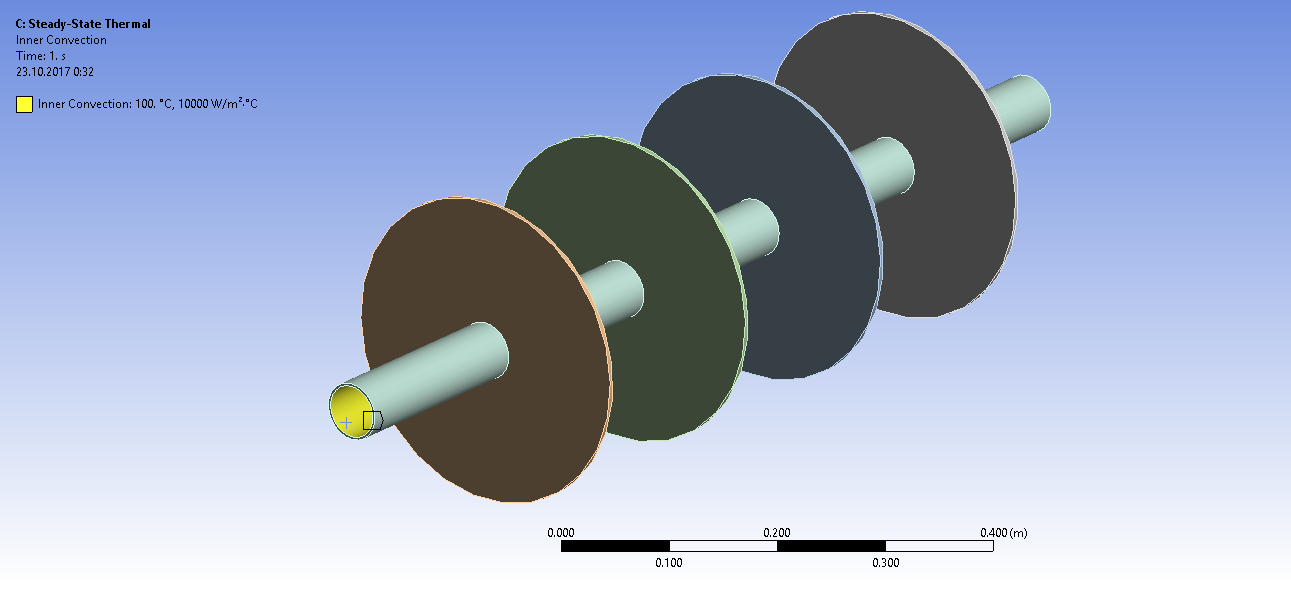
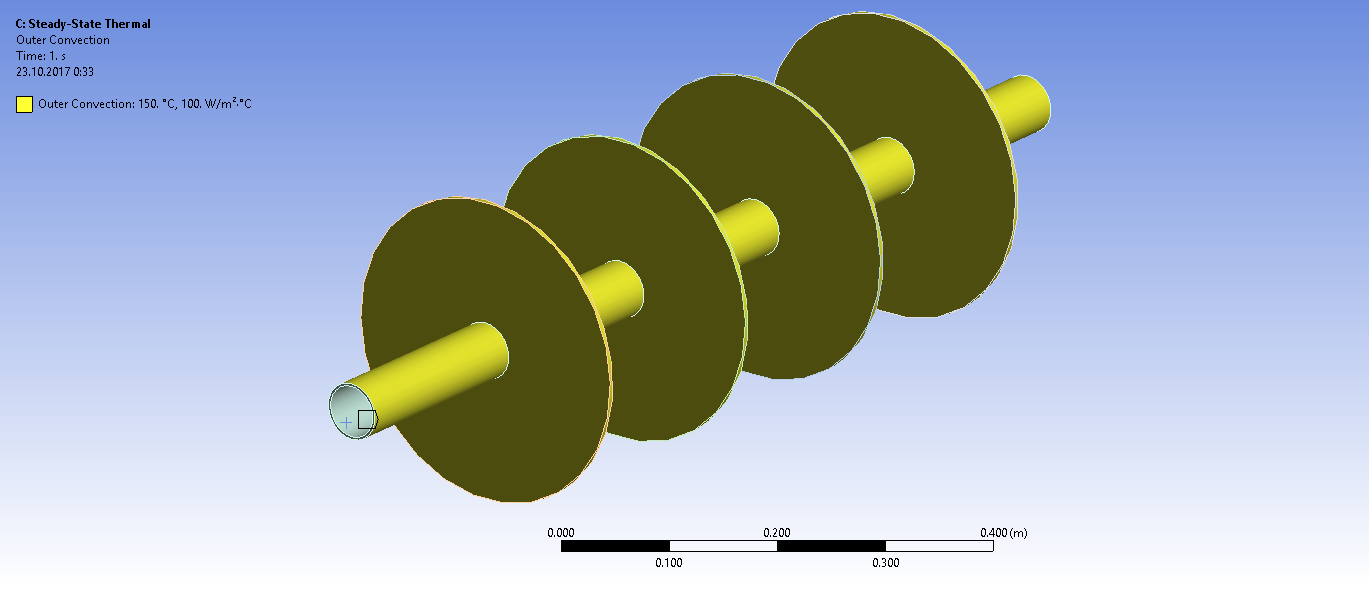
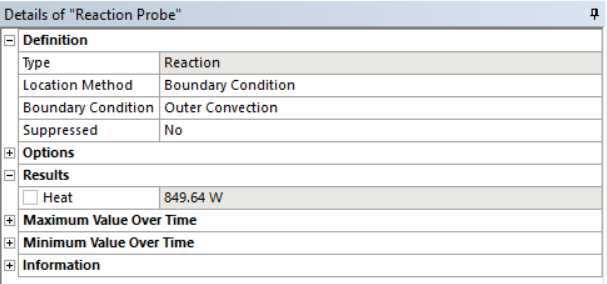
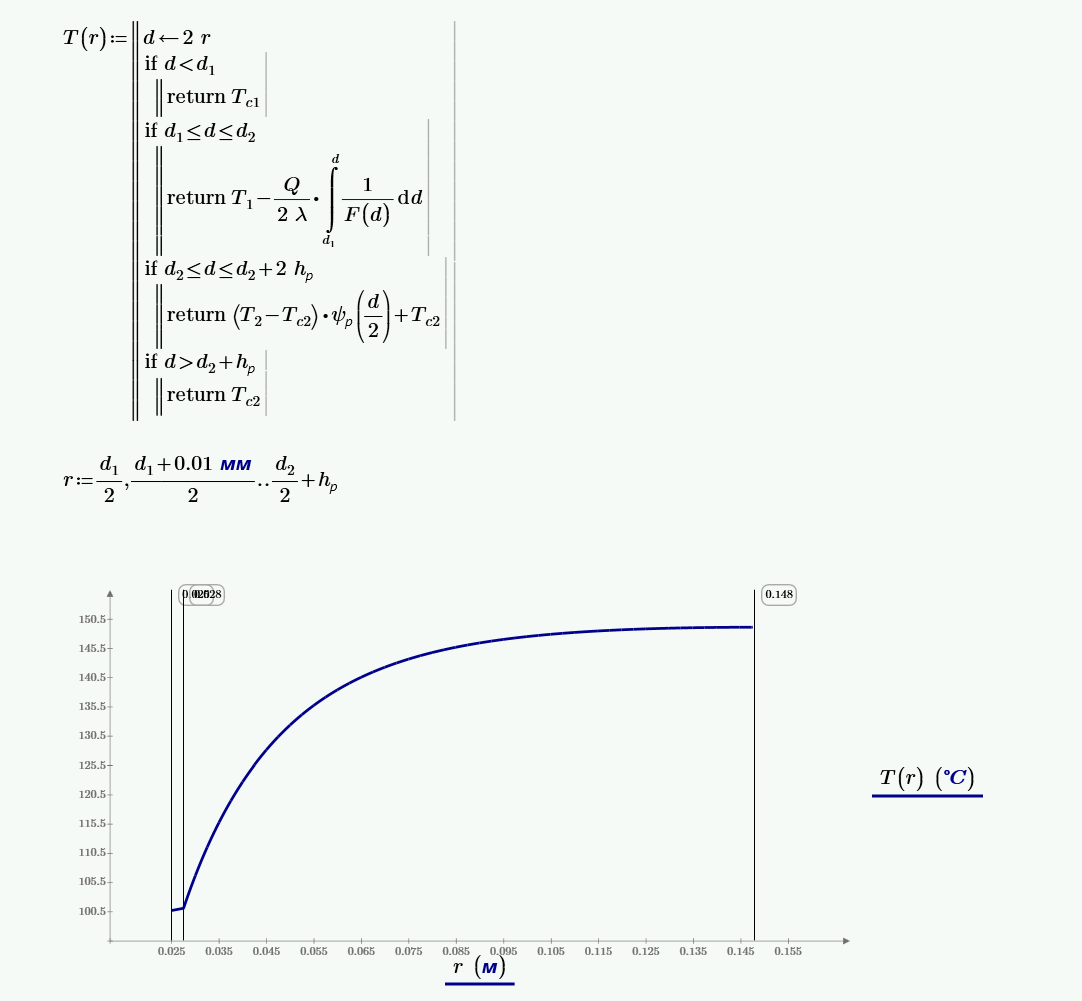
Получаем распределение температур
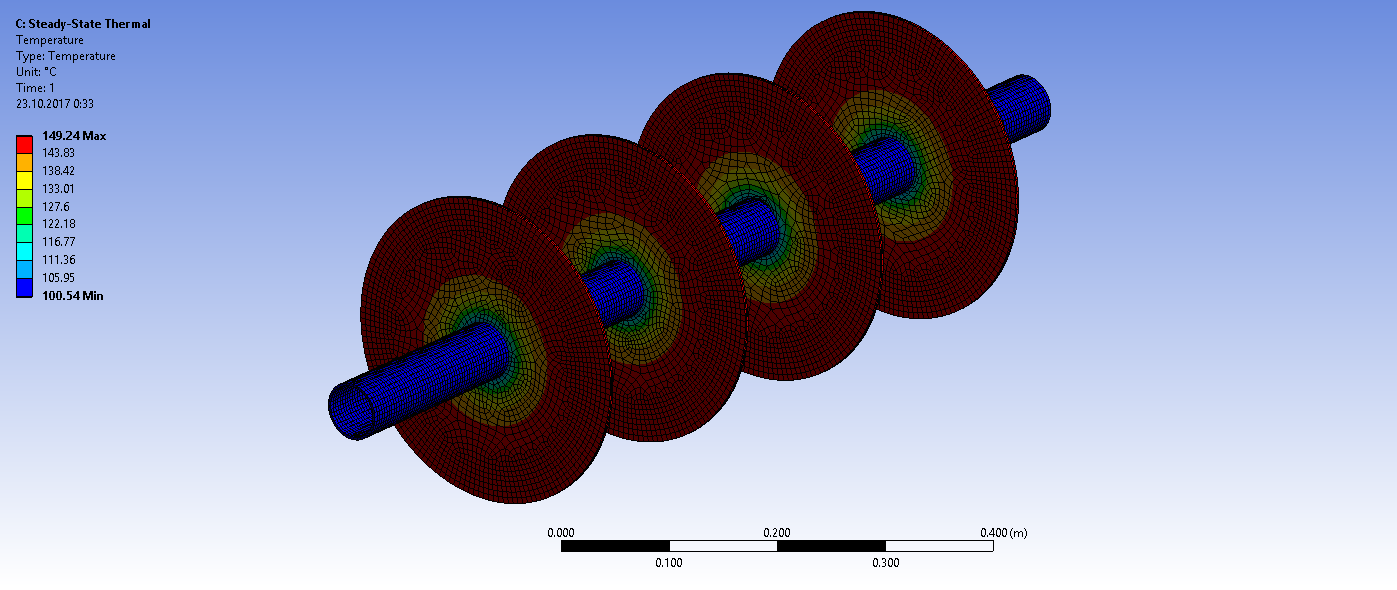
и удельный линейный тепловой поток через поверхность трубы с учетом ребер
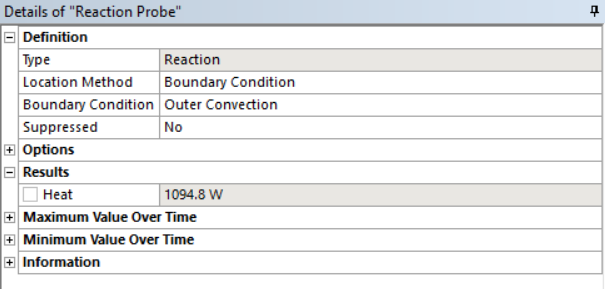
Создаем модель трубы без ребер

Создаем сетку
Задаем граничные условия конвективного теплообмена внутри трубы и снаружи

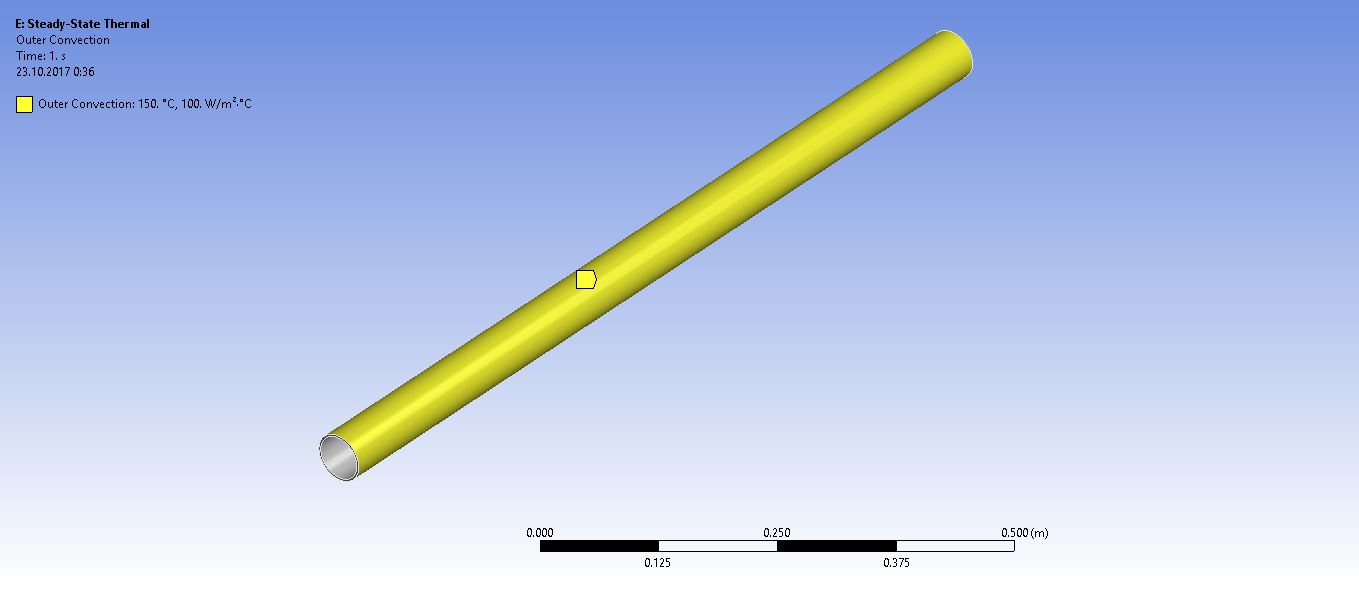
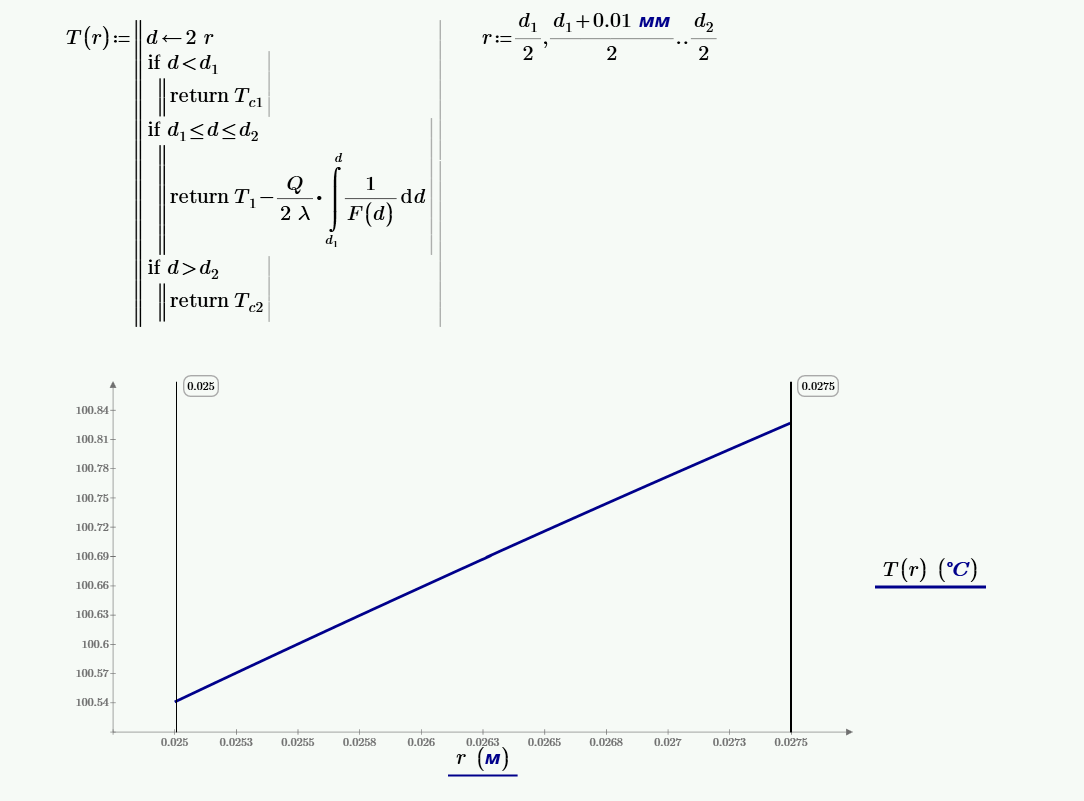
Получаем распределение температур
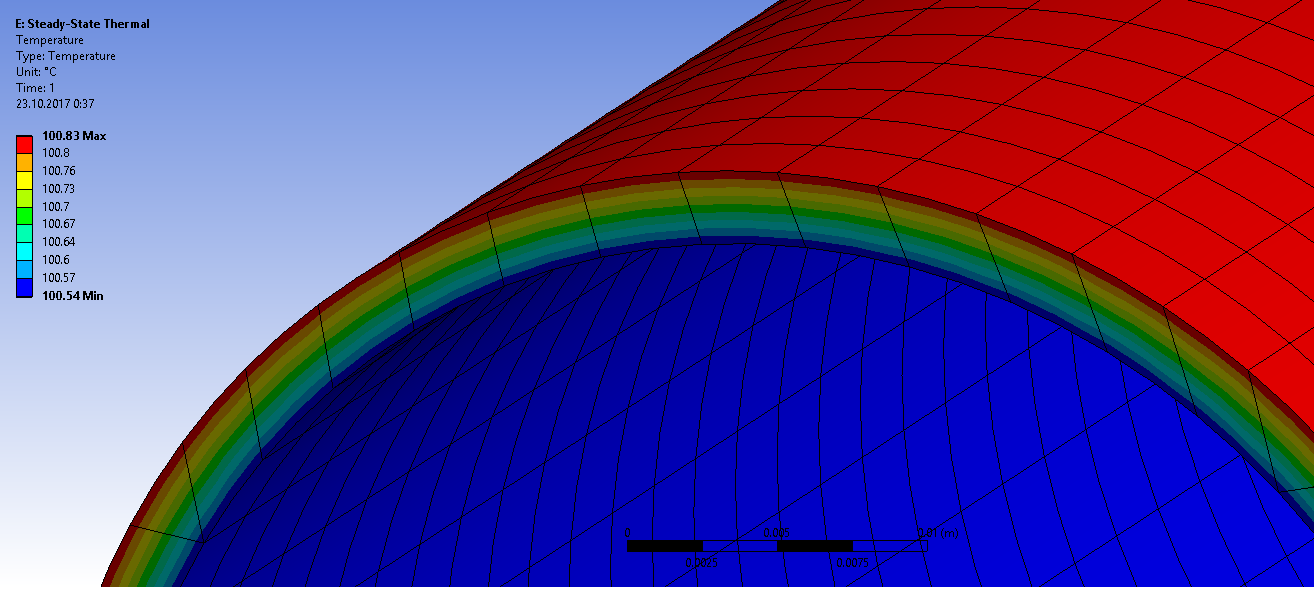
и удельный линейный тепловой поток через поверхность трубы без учета ребер