Определить температуры в центре и на поверхности шара диаметром $d = 30$ мм, через $\tau = 4$ минут после начала охлаждения, начальная температура $t_0 = 150$ °C, температура окружающего воздуха $t_ж = 40$ °C, коэффициент теплопроводности материала $\lambda = 1$ Вт/м·К, коэффициент температуропроводности $a = 0.6·10^{-6}$ м2/с, коэффициент теплоотдачи на поверхности пластины и стержня $\alpha = 100$ Вт/м2·К. Определить максимальную разность температур между серединой и поверхностью $\Delta t_{max}$.
Число Био:
$$Bi=\frac{\frac{d}{2·\lambda}}{\frac{1}{\alpha}} = \frac{\frac{0.03}{2·1}}{\frac{1}{100}} = 1.5.$$Числа подобия по таблице в зависимости от числа Био: $\mu_1 = 1.83$, $\mu_2 = 4.81$, $A_1 = 1.38$, $A_2 = -0.60$.
Число Фурье:
$$Fo = \frac{a·\tau}{\left(\frac{d}{2}\right)^2} = \frac{0.6·10^{-6}·240}{\left(\frac{0.03}{2}\right)^2} = 0.64.$$Для расчета используется два члена ряда:
$$\theta(R) = A_1·\frac{\sin{(\mu_1·R)}}{\mu_1·R}·\exp{(-\mu_1^2·Fo)}+A_2·\frac{\sin{(\mu_2·R)}}{\mu_2·R}·\exp{(-\mu_2^2·Fo)}.$$В центре шара безразмерный радиус равен $R = 0$, тогда безразмерная температура равна:
$$\theta(R=0) = 1.38·\exp{(-1.83^2·0.64)}+(-0.60)·\exp{(-4.81^2·0.64)} = 0.16.$$Температура в центре, °C:
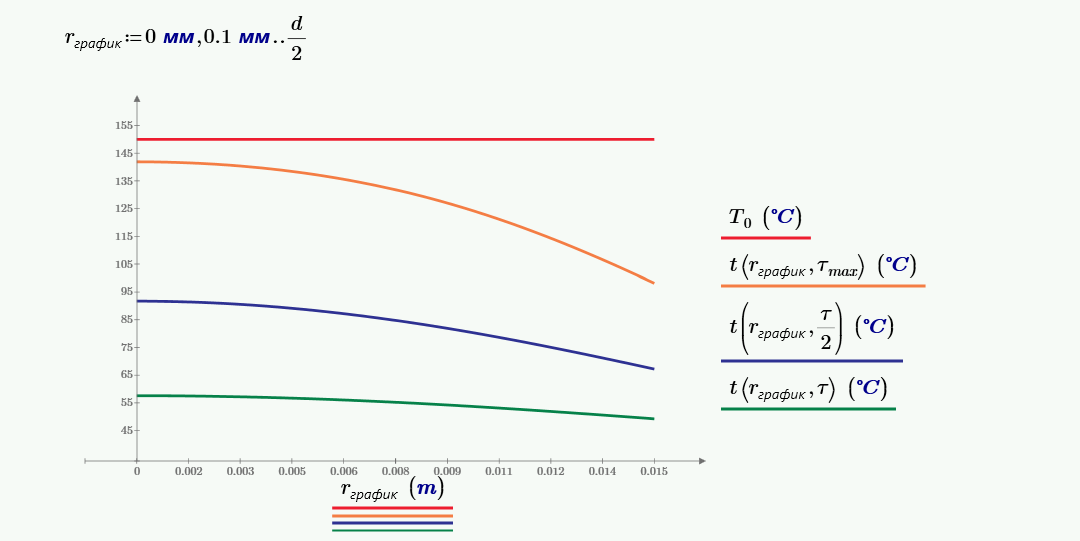
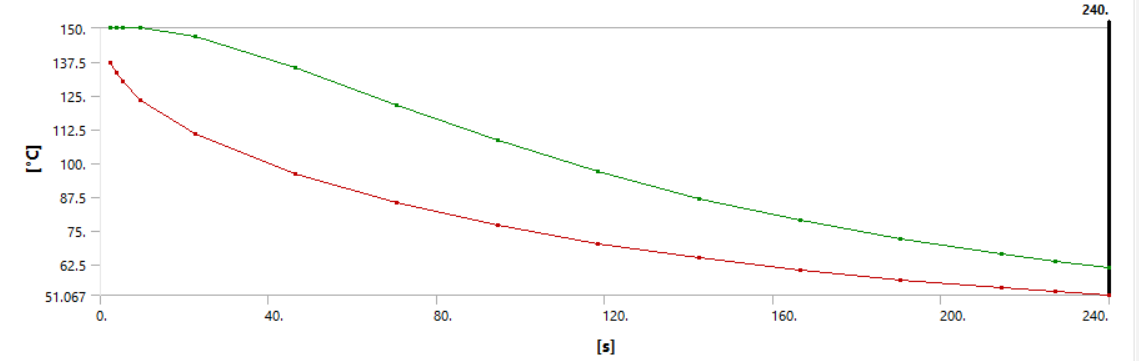
$$t(R=0) = \theta(R=0)·(t_0-t_ж)+t_ж = 0.16·(150-40)+40 = 57.$$На поверхности шара безразмерный радиус равен $R=1$, тогда безразмерная температура равна:
$$\theta(R=1) = 1.38·\frac{\sin{(1.83·1)}}{1.83·1}·\exp{(-1.83^2·0.64)}+(-0.60)·\frac{\sin{(4.81·1)}}{4.81·1}·\exp{(-4.81^2·0.64)} = 0.084.$$Температура в центре, °C:
$$t(R=1) = \theta(R=1)·(t_0-t_ж)+t_ж = 0.084·(150-40)+40 = 49.$$Находим максимальную разность температур между центром и поверхностью:
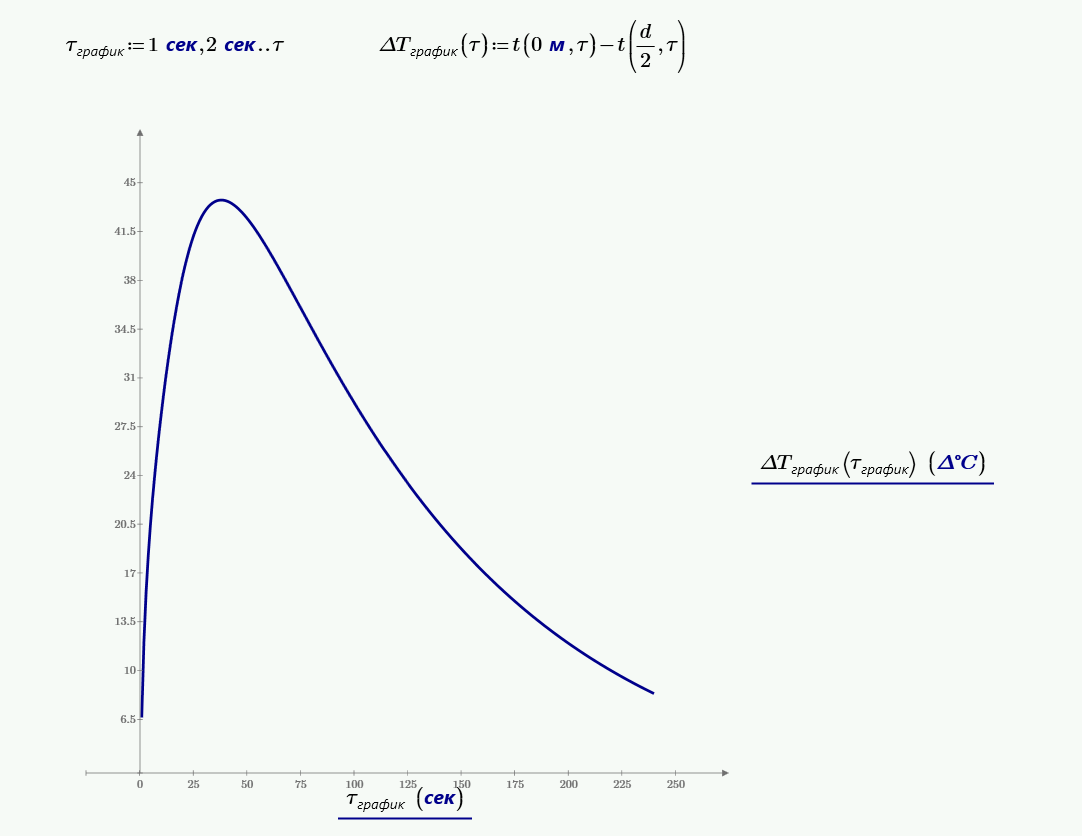
$$\frac{\partial (\theta(R=0)-\theta(R=1))}{\partial Fo} = 0.$$Или
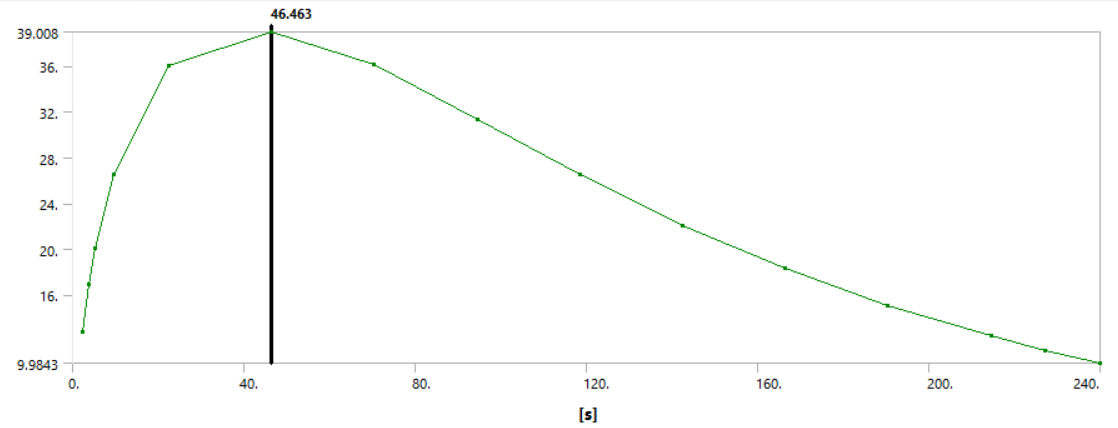
$$\frac{\partial (\theta(1.38·\exp{(-1.83^2·Fo)}+(-0.60)·\exp{(-4.81^2·Fo)})-\theta(1.38·\frac{\sin{(1.83·1)}}{1.83·1}·\exp{(-1.83^2·Fo)}+(-0.60)·\frac{\sin{(4.81·1)}}{4.81·1}·\exp{(-4.81^2·Fo)}))}{\partial Fo} = 0.$$Откуда $Fo = 0.102$, то есть максимальная разница температур будет наблюдаться примерно через одну минуту после начала процесса.
В центре шара безразмерный радиус равен $R=0$, тогда безразмерная температура равна:
$$\theta(R=0) = 1.38·\exp{(-1.83^2·0.102)}+(-0.60)·\exp{(-4.81^2·0.102)} = 0.926.$$Температура в центре:
$$t(R=0) = \theta(R=0)·(t_0-t_ж)+t_ж = 0.926·(150-40)+40 = 141.$$На поверхности шара безразмерный радиус равен $R=1$, тогда безразмерная температура равна:
$$\theta(R=1) = 1.38·\frac{\sin{(1.83·1)}}{1.83·1}·\exp{(-1.83^2·0.102)}+(-0.60)·\frac{\sin{(4.81·1)}}{4.81·1}·\exp{(-4.81^2·0.102)} = 0.528.$$Температура в центре:
$$t(R=1) = \theta(R=1)·(t_0-t_ж)+t_ж = 0.528·(150-40)+40 = 98.$$Максимальная разница температур, °C:
$$\Delta t_{max} = t(R=0)-t(R=1) = 141 - 98 = 43.$$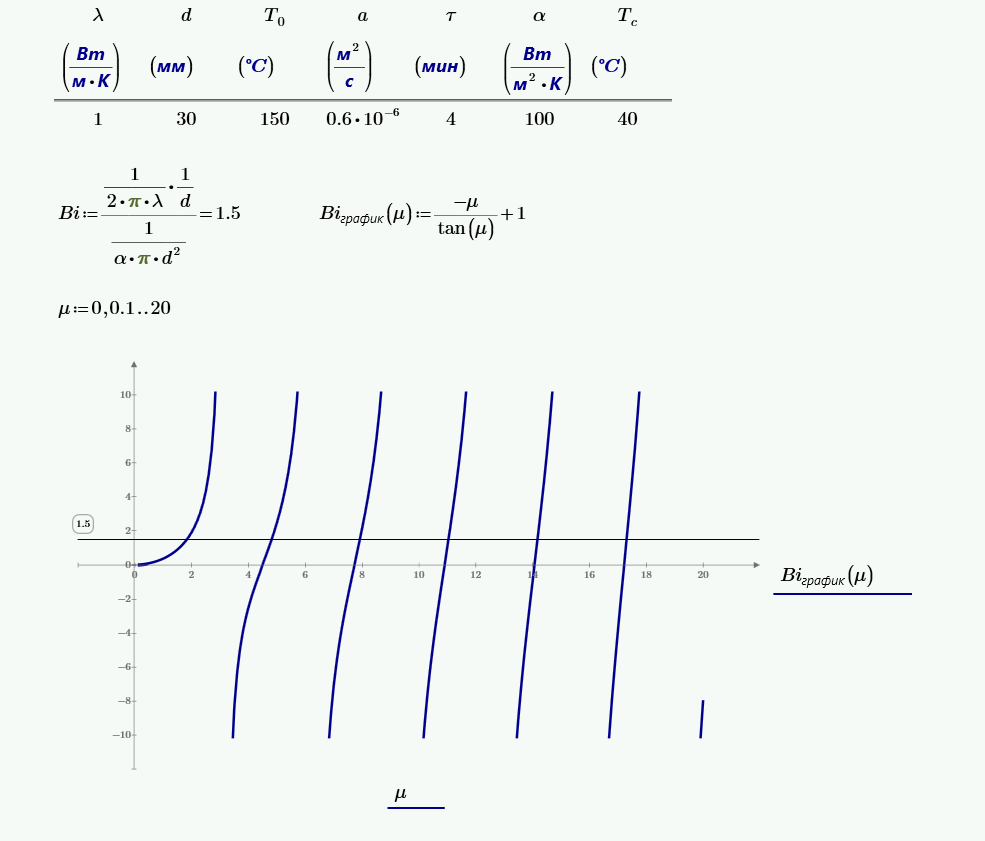


Создаем модель
Создаем сетку

Задаем граничные условия конвективного теплообмена на поверхности
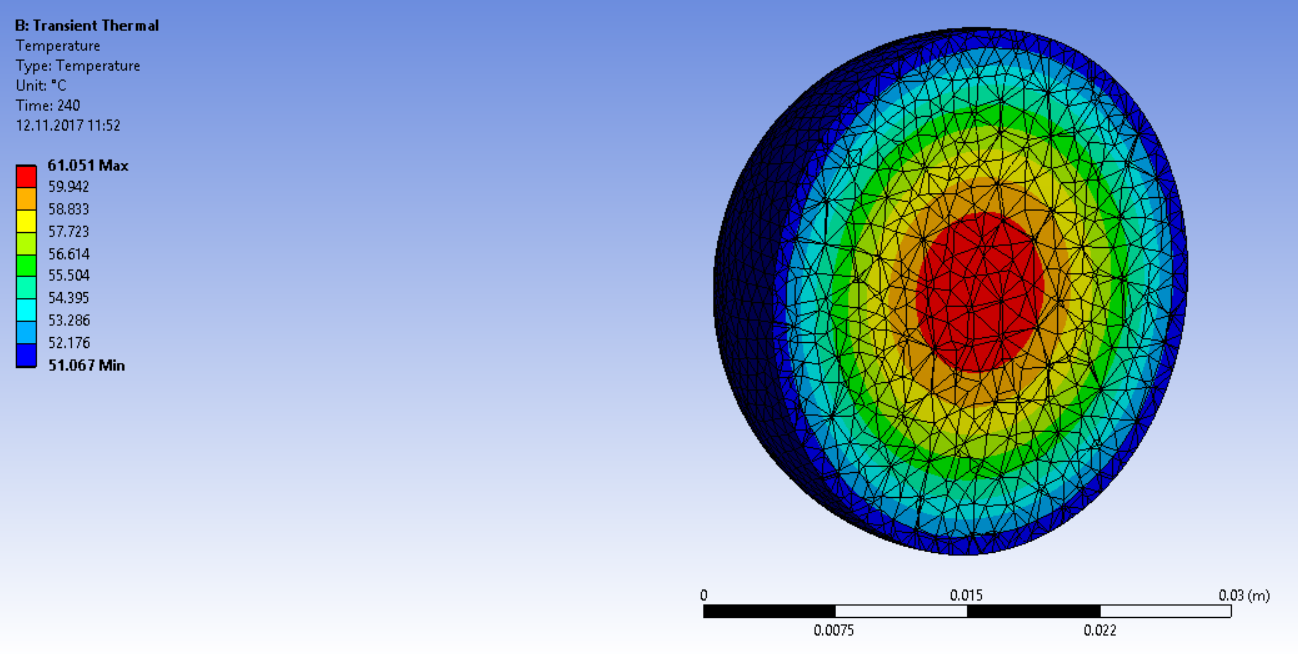
Получаем распределение температур по окончанию процесса
Получаем изменение максимальной и минимальной температур во времени
Получаем разность максимальной и минимальной температур во времени
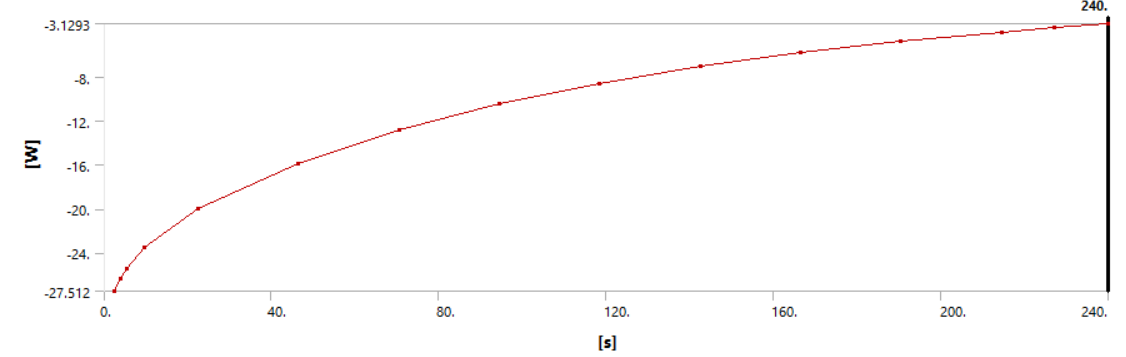
Получаем изменение теплового потока с поверхности шара во времени