Шар наружным диаметром $d_2 = 120$ мм с коэффициентом теплопроводности $\lambda = 65$ Вт/м·К подключен к источнику питания с напряжением $U = 360$ В и силой тока $I = 0.2$ А и охлаждается с обеих сторон. С внешней стороны на них наложена изоляция толщиной $\delta_{из} = 4$ мм и коэффициентом теплопроводности $\lambda_{из} = 0.12$ Вт/м·К. Температура охлаждающей жидкости $t_ж = 150$ °C и коэффициент теплоотдачи $\alpha = 1000$ Вт/м2·К. Определить максимальную температуру, температуры в центре стержня, на поверхностях трубопровода или стержня и изоляции.
Мощность внутренних источников тепла определяется, Вт/м3:
$$q_v = \frac{6·I·U}{\pi·d_2^3} = \frac{6·0.2·360}{\pi·0.12^3} = 8·10^4.$$Для упрощения задачи путем учета изоляции в качестве дополнительного термического сопротивления теплоотдачи, рассчитаем приведенный коэффициент теплоотдачи, Вт/м2·К:
$$\alpha_{пр} = \frac{1}{d_2^2}·\frac{1}{\frac{1}{\alpha·(d_2+2·\delta_{из})^2}+\frac{1}{2·\lambda_{из}}·\left(\frac{1}{d_2}-\frac{1}{d_2+2·\delta_{из}}\right)} = $$ $$ = \frac{1}{0.12^2}·\frac{1}{\frac{1}{1000·(0.12+2·0.004)^2}+\frac{1}{2·0.12}·\left(\frac{1}{0.12}-\frac{1}{0.12+2·0.004}\right)} = 31.$$Обратите внимание! В классической постановке задача решается с помощью двух дифференциальных уравнений с граничными условиями четвертого рода между слоями.
При указанных условиях температура шара будет изменяться только вдоль оси $r$, тогда дифференциальное уравнение принимает вид:
$$\frac{\partial^2 t}{\partial r^2} + \frac{2}{r}·\frac{\partial t}{\partial r} + \frac{q_v}{\lambda} = 0.$$Обратите внимание! Вид уравнения зависит от геометрии тела.
После интегрирования получим:
$$\frac{\partial t}{\partial r} = -\frac{q_v·r}{3·\lambda}+\frac{C_1}{r^2};$$ $$t = -\frac{q_v·r^2}{6·\lambda}-C_1·\frac{1}{r}+C_2.$$Постоянные интегрирования определяются из граничных условий.
при $r=0$
$$-\lambda·\frac{\partial t}{\partial r}=0;$$при $r=r_0 = d_2/2 = 0.06$
$$-\lambda·\frac{\partial t}{\partial r}=\alpha·(t-t_ж);$$Тогда:
$$\lambda·\left(-\frac{q_v·0}{3·\lambda}+\frac{C_1}{0}\right) = 0;$$ $$-\lambda·\left(-\frac{q_v·r_0}{3·\lambda}+\frac{C_1}{r_0^2}\right) = \alpha_{пр}·\left(\left(-\frac{q_v·r_0^2}{6·\lambda}-C_1·\frac{1}{r_0}+C_2\right)-t_ж\right).$$Или
$$65·\left(-\frac{8·10^5·0}{3·65}+\frac{C_1}{0}\right) = 0;$$ $$-\lambda·\left(-\frac{8·10^5·0.06}{3·65}+\frac{C_1}{0.06^2}\right) = 31·\left(\left(-\frac{8·10^5·0.06^2}{6·65}-C_1·\frac{1}{0.06}+C_2\right)-150\right).$$Решая систему находим: $C_1 = 0$; $C_2 = 201.8$.
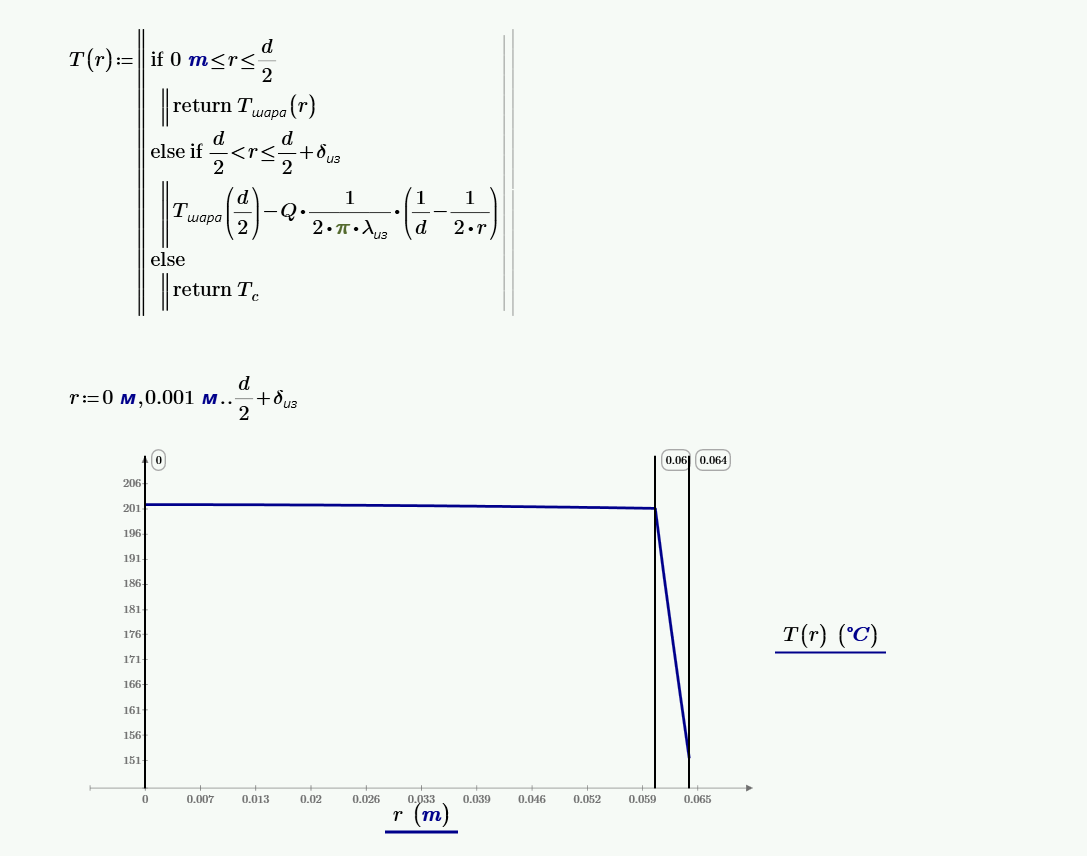
Задаем распределение температуры внутри шара:
$$t = -\frac{q_v·r^2}{6·\lambda}-C_1·\frac{1}{r}+C_2 = -\frac{8·10^5·r^2}{6·65}-0·\frac{1}{r}+201.8 = -\frac{8·10^5·r^2}{6·65}+201.8.$$Находим температуры в середине и на краях шара:
при $r = 0$ м температура равна $t(0) = 201.8$ °C;
при $r = d_2/4 = 0.03$ м температура равна $t(0.03) = 201.6$ °C;
при $r = r_0 = d_2/2 = 0.06$ м температура равна $t(0.06) = 201.1$ °C;
Находим максимальную температуру используя свойства экстремумом:
при $\partial t/\partial r = 0$ находим $r_{max} = 0$ м;
при $r = r_{max} = 0$ м температура равна $t_{max}(0) = 201.8$ °C.
Находим температуру поверхности изоляции:
$$\frac{\pi·(t(r_0)-t_{из})}{\frac{1}{2·\lambda_{из}}·\left(\frac{1}{d_2}-\frac{1}{d_2+2·\delta_{из}}\right)} = \alpha·\pi·(d_2+2·\delta_{из})·(t_{из}-150);$$ $$\frac{\pi·(201.8-t_{из})}{\frac{1}{2·0.12}·\left(\frac{1}{0.12}-\frac{1}{0.12+2·0.004}\right)} = 1000·\pi·(0.12+2·0.004)·(t_{из}-150);$$Откуда температура изоляции равна $t_{из} = 151.4$°С.

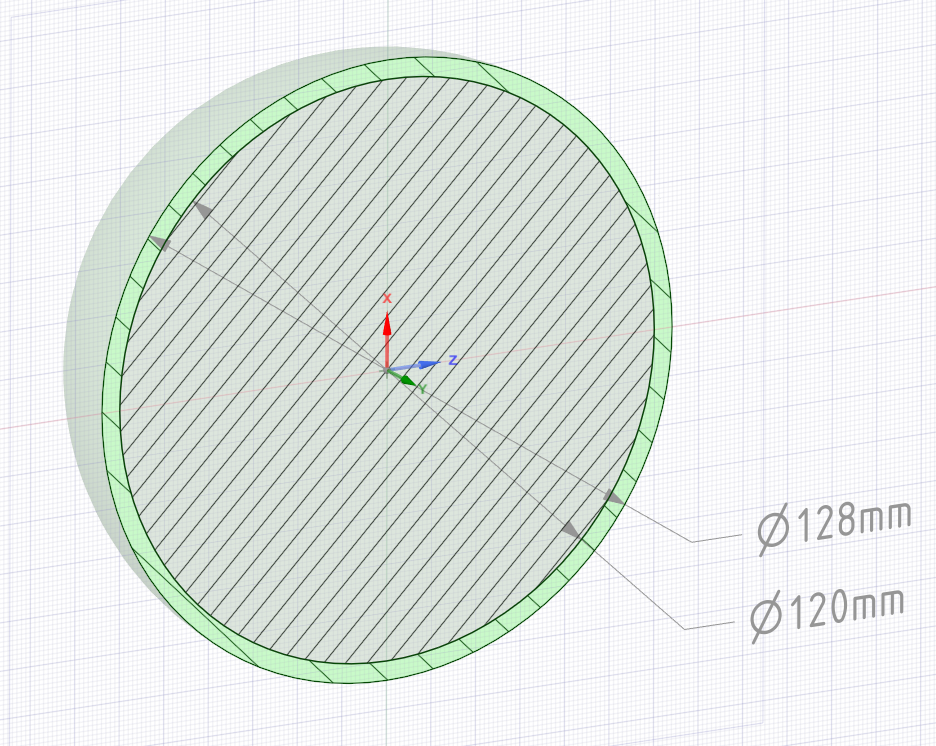
Создаем модель
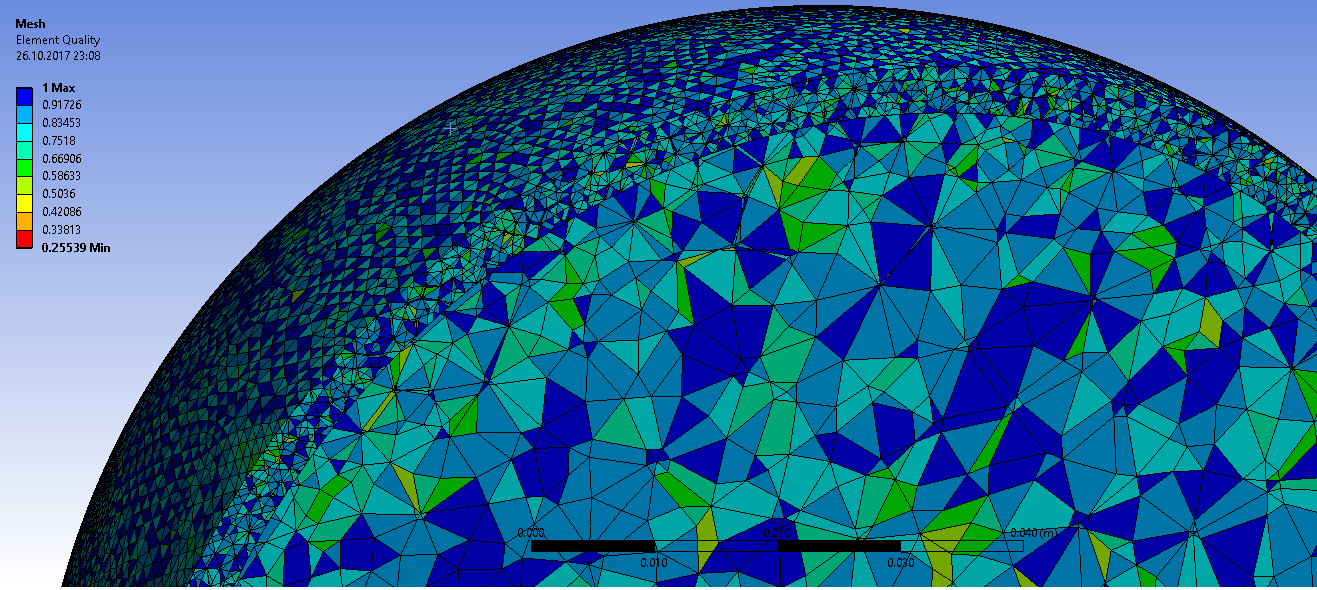
Создаем сетку
Задаем внутренние источники тепла
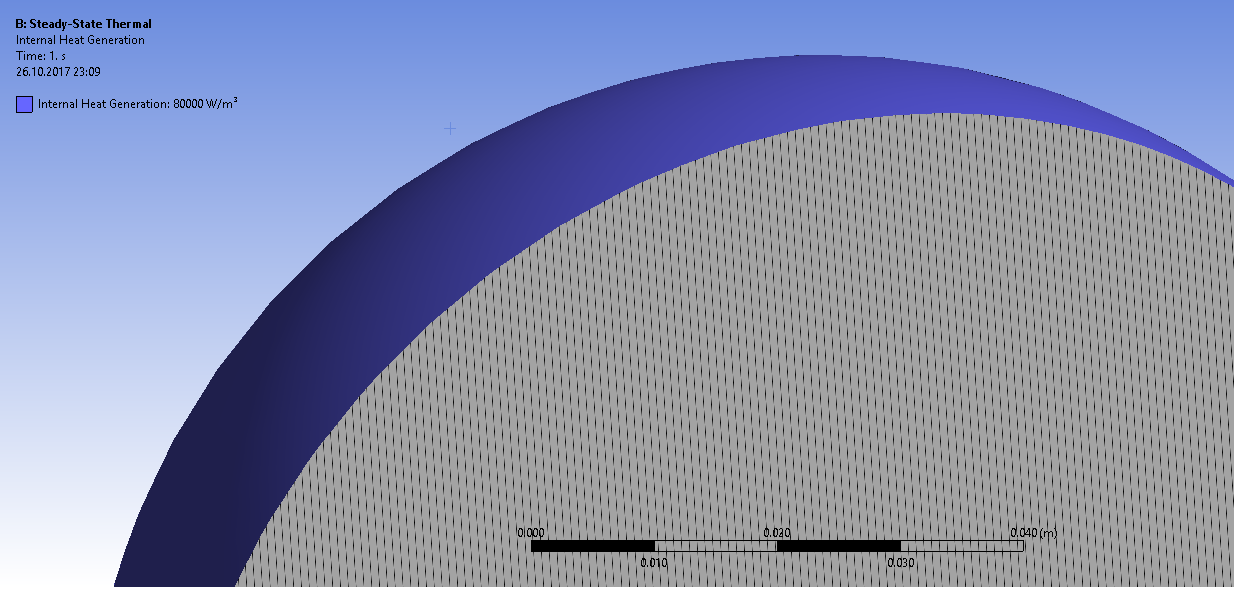
Задаем граничные условия конвективного теплообмена на поверхности изоляции
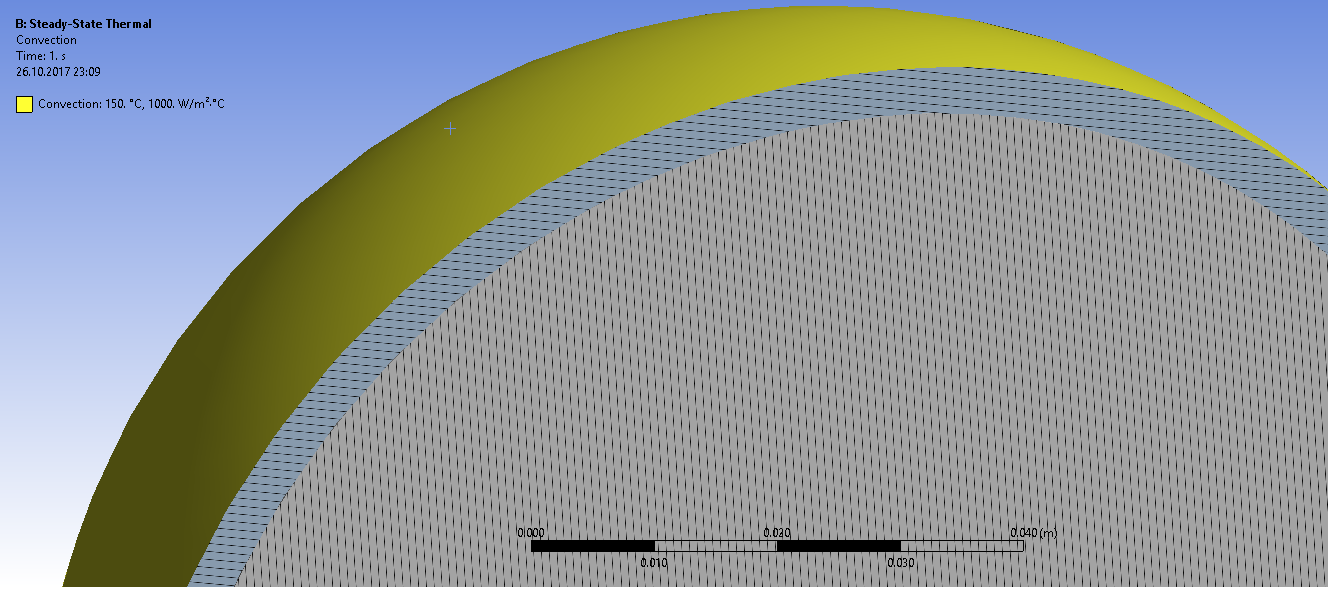
Получаем распределение температур
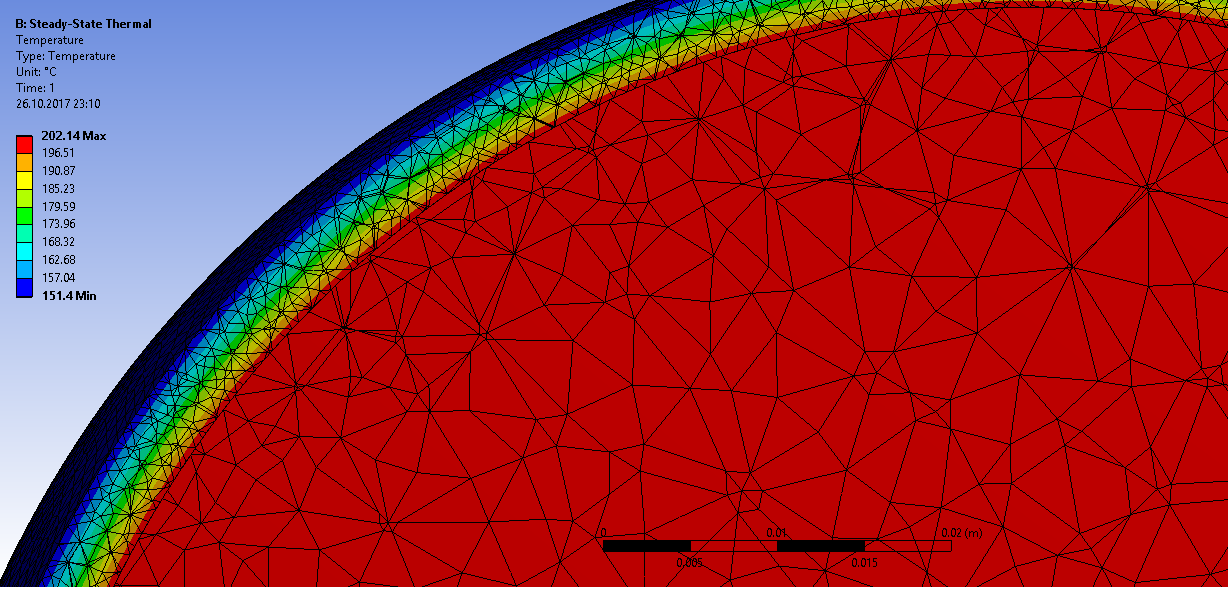
и тепловой поток