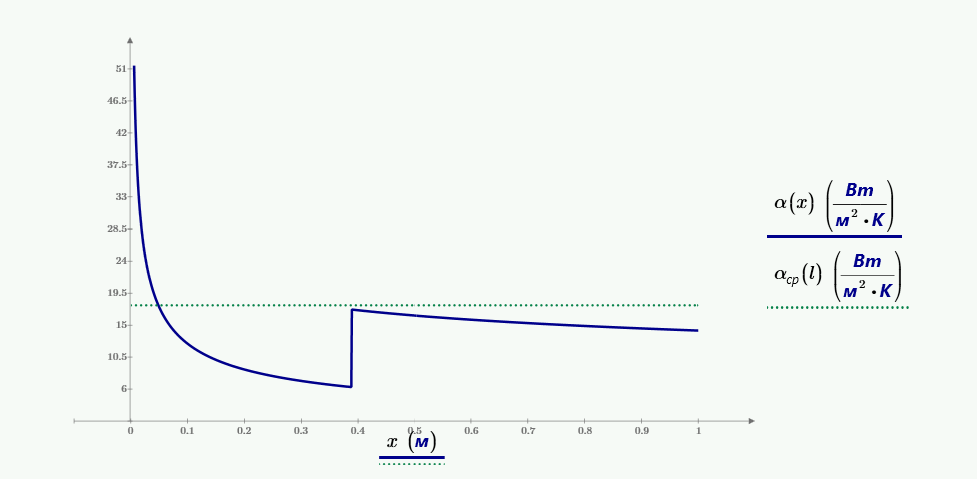
Тонкая квадратная пластина расположенная вертикально со стороной $l = 1$ м охлаждается потоком воздуха со скоростью $\omega = 4$ м/с и температурой $t_ж = 25$ °C. К краям пластины приложено напряжение $U = 360$ и протекает ток $I = 2$ А. Определить местные коэффициенты теплоотдачи и температуры поверхности на расстоянии $0.1·l$, $0.2·l$, $0.5·l$, $l$ от переднего края пластины, средний коэффициент теплоотдачи, тепло отводимое от пластины и построить график изменения коэффициента теплоотдачи. Решить задачу при условии свободного охлаждения.
При описании процесса конвективного теплообмена используется уравнение теплоотдачи Ньютона-Рихмана:
$$q = \alpha·(t_c - t_ж).$$Плотность теплового потока находиться из уравнения, Вт/м2:
$$q = \frac{I·U}{L^2} = \frac{2·360}{1^2} = 720.$$Вынужденная конвекция.
Для определения режима течения воздуха используется число Рейнольдса:
$$Re = \frac{\omega·l}{\nu_ж}.$$Свойства воздуха находятся из таблицы «Физические свойства сухого воздуха» при температуре воздуха:
| $t$, °C | $\lambda$, Вт/м·К | $\nu$, м2/с | $Pr$ |
|---|---|---|---|
| $25$ | $2.59·10^{-2}$ | $15.06·10^{-6}$ | $0.703$ |
Определяем расстояние, на котором происходит изменение режима из условия:
$$Re = 10^5.$$Тогда расстояние равно, м:
$$l_{кр} = \frac{Re·\nu_ж}{\omega} = \frac{10^5·15.06·10^{-6}}{4} = 0.388.$$Определяем число Рейнольдса для всех случаев:
При $l = 0.1·l = 0.1$ м. Режим течения – ламинарный.
$$Re = \frac{4·0.1}{15.06·10^{-6}} = 2.576·10^4 < 10^5.$$При $l = 0.2·l = 0.2$ м. Режим течения – ламинарный.
$$Re = \frac{4·0.2}{15.06·10^{-6}} = 5.151·10^4 < 10^5.$$При $l = 0.5·l = 0.5$ м. Режим течения – турбулентный.
$$Re = \frac{4·0.5}{15.06·10^{-6}} = 1.288·10^5 > 10^5.$$При $l = 1·l = 1$ м. Режим течения – турбулентный.
$$Re = \frac{4·1}{15.06·10^{-6}} = 2.576·10^5 > 10^5.$$Для определения коэффициентов теплоотдачи, находим числа Нуссельта (поправкой Михеева для воздуха можно пренебречь):
При $l = 0.1·L$. Режим течения – ламинарный.
$$Nu = 0.33·Re^{0.5}·Pr^{0.33} = 0.33·(2.576·10^4)^{0.5}·0.703^{0.33} = 47.1.$$При $l = 0.2·L$. Режим течения – ламинарный.
$$Nu = 0.33·Re^{0.5}·Pr^{0.33} = 0.33·(5.151·10^4)^{0.5}·0.703^{0.33} = 66.5.$$При $l_{кр} = 0.388$. Режим течения – ламинарный.
$$Nu = 0.33·Re^{0.5}·Pr^{0.33} = 0.33·(10^5)^{0.5}·0.703^{0.33} = 92.7.$$При $l_{кр} = 0.388$. Режим течения – турбулентный.
$$Nu = 0.0296·Re^{0.8}·Pr^{0.43} = 0.0296·(10^5)^{0.8}·0.703^{0.43} = 253.$$При $l = 0.5·L$. Режим течения – турбулентный.
$$Nu = 0.0296·Re^{0.8}·Pr^{0.43} = 0.0296·(1.288·10^5)^{0.8}·0.703^{0.43} = 311.$$При $l = L$. Режим течения – турбулентный.
$$Nu = 0.0296·Re^{0.8}·Pr^{0.43} = 0.0296·(2.576·10^5)^{0.8}·0.703^{0.43} = 541.$$При $l = L$. Режим течения – турбулентный
$$\overline{Nu} = 0.037·Re^{0.8}·Pr^{0.43} = 0.037·(2.576·10^5)^{0.8}·0.703^{0.43} = 676.$$Коэффициент теплоотдачи находиться по формуле, Вт/м2·К:
$$\alpha = \frac{Nu·\lambda_ж}{l}.$$При $l = 0.1·L$.
$$\alpha = \frac{47.1·2.59·10^{-2}}{0.1} = 12.4.$$При $l = 0.2·L$.
$$\alpha = \frac{66.5·2.59·10^{-2}}{0.2} = 8.75.$$При $l_{кр} = 0.388$.
$$\alpha = \frac{92.7·2.59·10^{-2}}{0.388} = 6.18.$$При $l_{кр} = 0.388$.
$$\alpha = \frac{253·2.59·10^{-2}}{0.388} = 16.8.$$При $l = 0.5·L$.
$$\alpha = \frac{311·2.59·10^{-2}}{0.5} = 16.1.$$При $l = L$.
$$\alpha = \frac{541·2.59·10^{-2}}{1} = 14.0.$$При $l = L$.
$$\overline{\alpha} = \frac{676·2.59·10^{-2}}{1} = 17.5.$$Температура стенки находиться по формуле, °C:
$$t_c = \frac{q}{\alpha} + t_ж.$$При $l = 0.1·L$.
$$t_c = \frac{720}{12.4} + 25 = 83.$$При $l = 0.2·L$.
$$t_c = \frac{720}{8.75} + 25 = 107.$$При $l_{кр} = 0.388$.
$$t_c = \frac{720}{6.18} + 25 = 141.$$При $l_{кр} = 0.388$.
$$t_c = \frac{720}{16.8} + 25 = 67.$$При $l = 0.5·L$.
$$t_c = \frac{720}{16.1} + 25 = 69.$$При $l = L$.
$$t_c = \frac{720}{14} + 25 = 76.$$При $l = L$.
$$\overline{t_c} = \frac{720}{17.5} + 25 = 66.$$Свободная конвекция.
Ламинарный режим заканчивается при:
$$Gr·Pr_ж = \frac{g·\beta·(t_c-t_ж)·l^3}{\nu_ж^2} = 10^9$$и
$$q = \frac{0.6·(10^9)^{0.25}·\lambda_ж}{l}(t_c-t_ж).$$отсюда находим расстояние до точки перехода, а также температуру стенки $l_{кр} = 0.2$ м и $t_c = 116$ °C.
Коэффициент теплоотдачи находиться по формуле:
$$\alpha = \frac{0.6·(10^9)^{0.25}·\lambda_ж}{l} = \frac{0.6·(10^9)^{0.25}·0.0269}{0.2} = 7.95.$$Турбулентный режим начинается при:
$$Gr·Pr_ж = \frac{g·\beta·(t_c-t_ж)·l^3}{\nu_ж^2} = 6·10^{10}$$и
$$q = \frac{0.15·(6·10^{10})^{0.33}·\lambda_ж}{l}(t_c-t_ж).$$отсюда находим расстояние до точки перехода, а также температуру стенки $l_{кр} = 1.8$ м и $t_c = 120$ °C.
Коэффициент теплоотдачи находиться по формуле:
$$\alpha = \frac{0.15·(6·10^{10})^{0.33}·\lambda_ж}{l} = \frac{0.15·(6·10^{10})^{0.33}·0.0269}{0.2} = 7.61.$$Ищем точки, не вошедшие в переходную зону – в данном случае это одна единственная точка $l = 0.1·L$. Для нахождения значения коэффициента теплоотдачи, запишем число Грасгофа
$$Gr = \frac{g·\beta·(t_c-t_ж)·l^3}{\nu_ж^2} = \frac{g·\frac{1}{25+273.15}·(t_c-25)·0.1^3}{(15.06·10^{-6})^2} = 14620·(t_c - 25).$$Для определения коэффициентов теплоотдачи, находим числа Нуссельта (из условия $0.1·L < 0.2$ узнаем, что режим течения ламинарный):
$$Nu = 0.6·(Gr·Pr)^{0.25} = 0.6·(14620·(t_c - 25)·0.703)^{0.25} = 6.04·(t_c-25)^{0.25}.$$Коэффициент теплоотдачи находиться по формуле:
$$\alpha = \frac{Nu·\lambda_ж}{l} = \frac{6.04·(t_c-25)^{0.25}·0.0259}{0.1} = 1.56·(t_c-25)^{0.25}.$$Из уравнения Ньютона-Рихмана находим температуру стенки:
$$q = \alpha·(t_c - t_ж) = 1.56·(t_c-25)^{0.25}·(t_c - 25) = 720.$$Тогда температура стенки равна $t_c = 70$ °C.
Коэффициент теплоотдачи находиться по формуле, Вт/м2·К:
$$\alpha = 1.56·(t_c-25)^{0.25} = 1.56·(70-25)^{0.25} = 10.$$


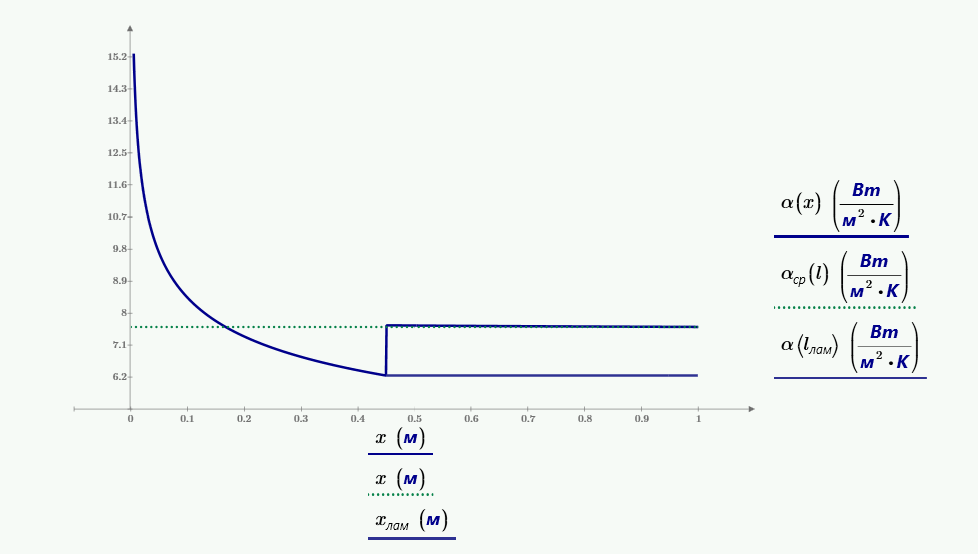
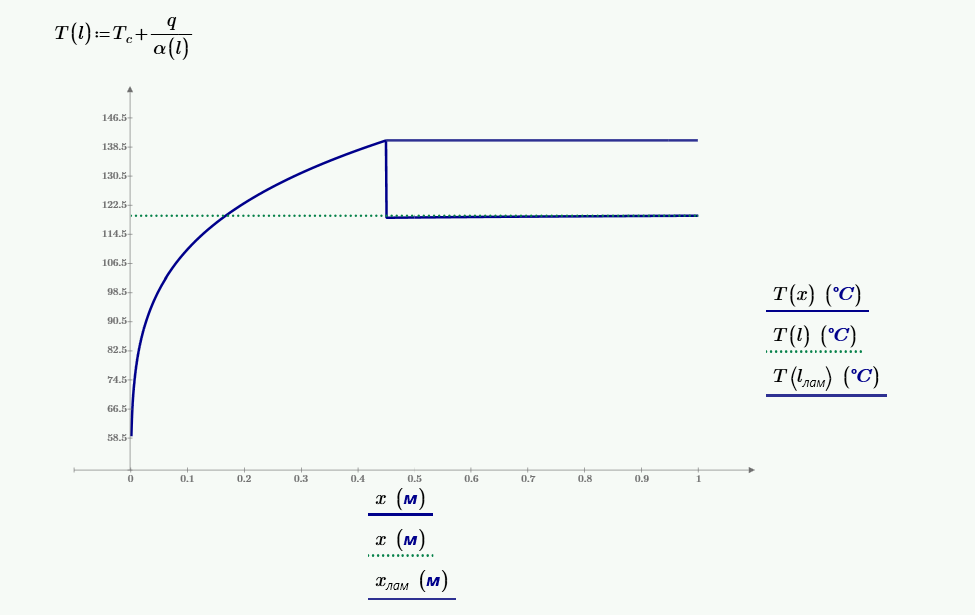
Создаем модель для воздушного пространства
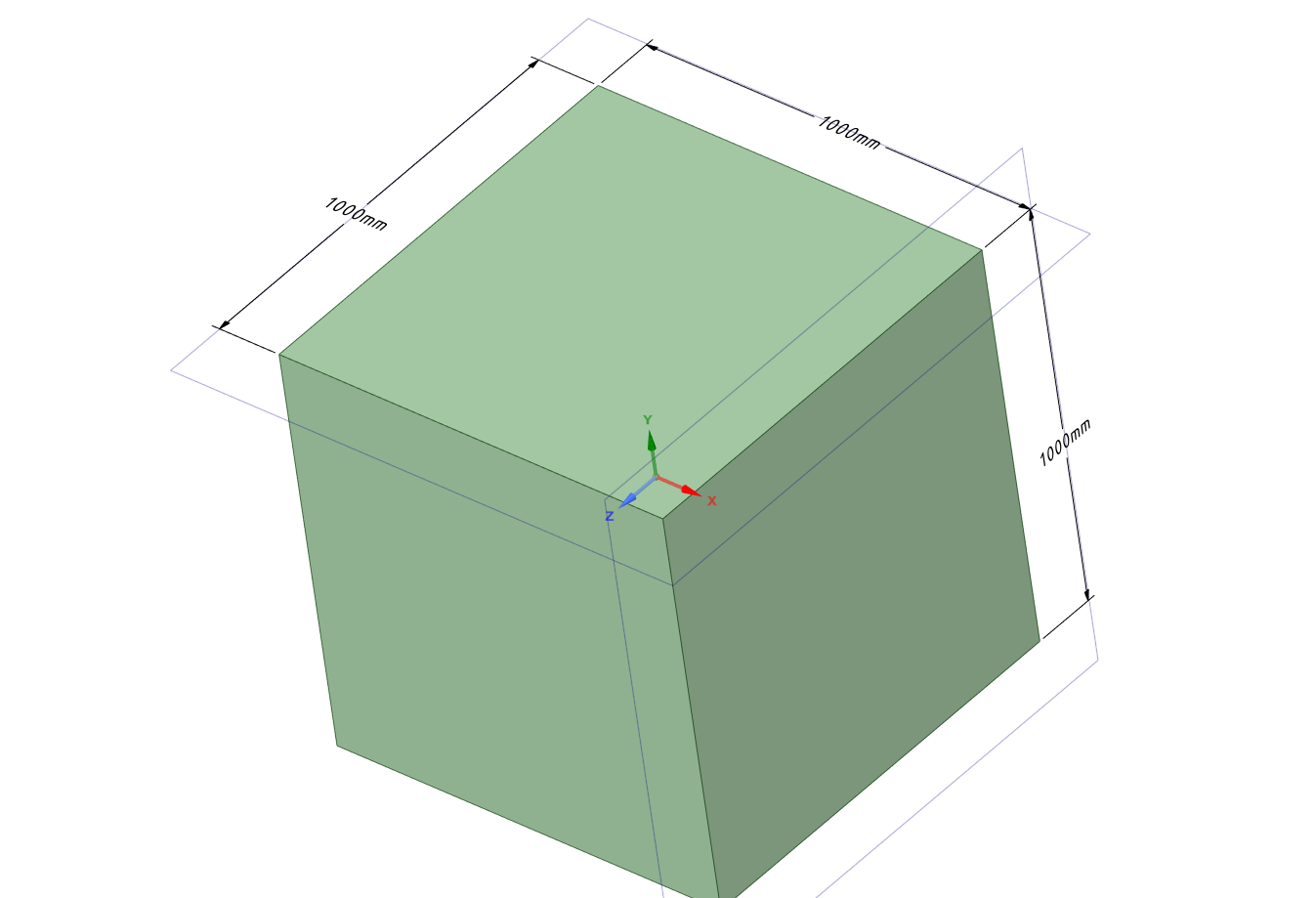
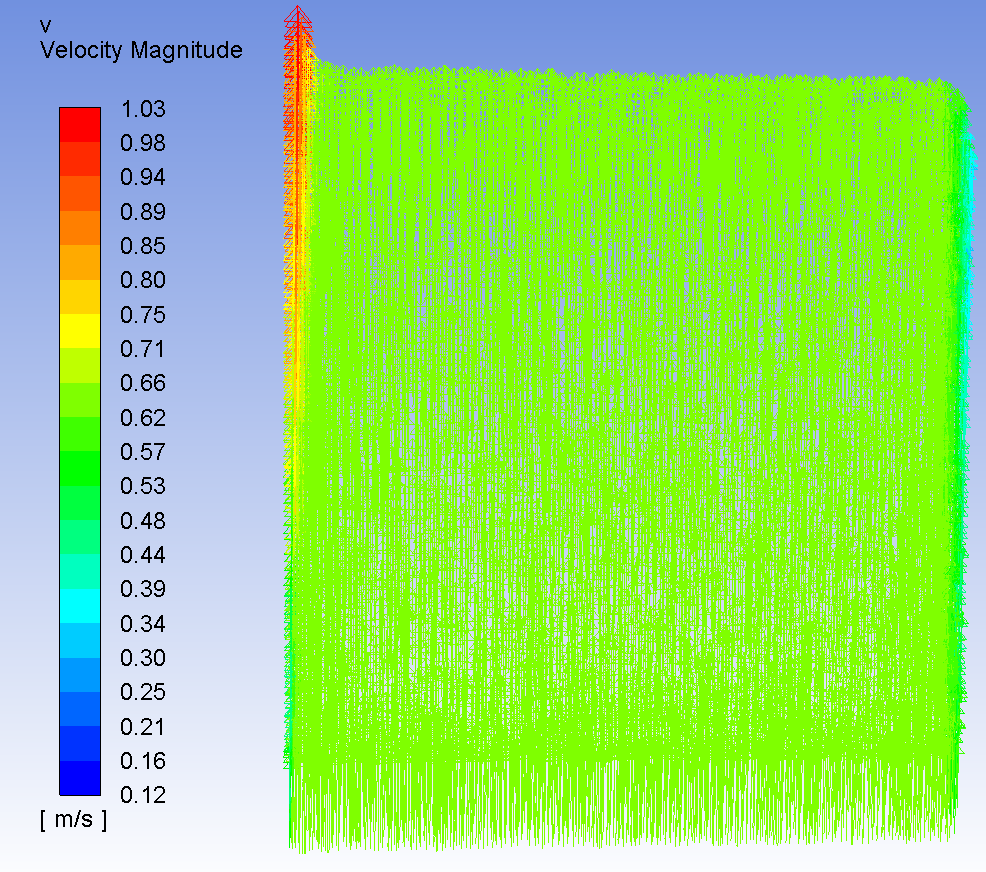
Производим расчет для вынужденного течения. Получаем распределение температуры для воздушного пространства (греющая пластина расположена слева)

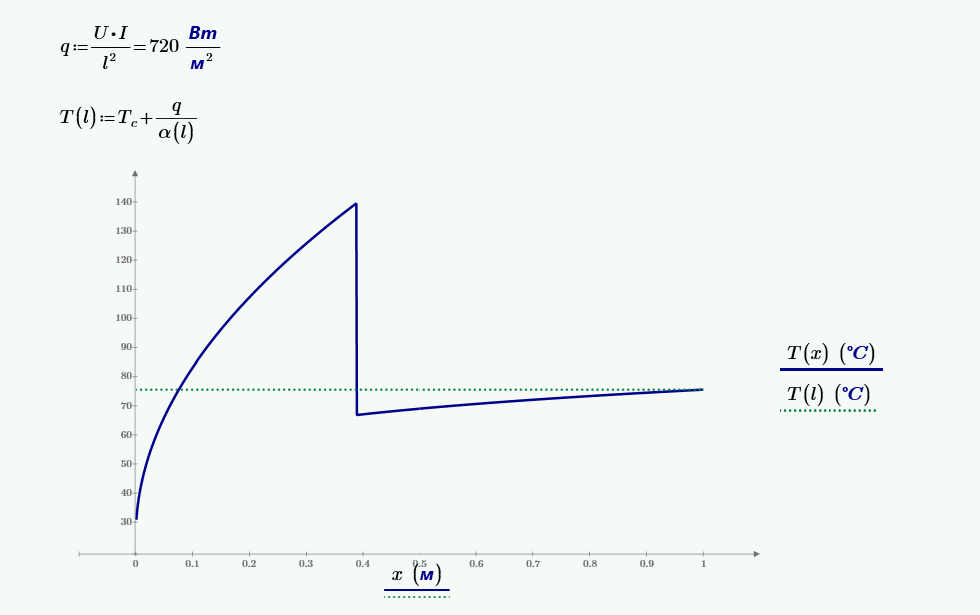
Получаем распределение температуры для поверхности пластины
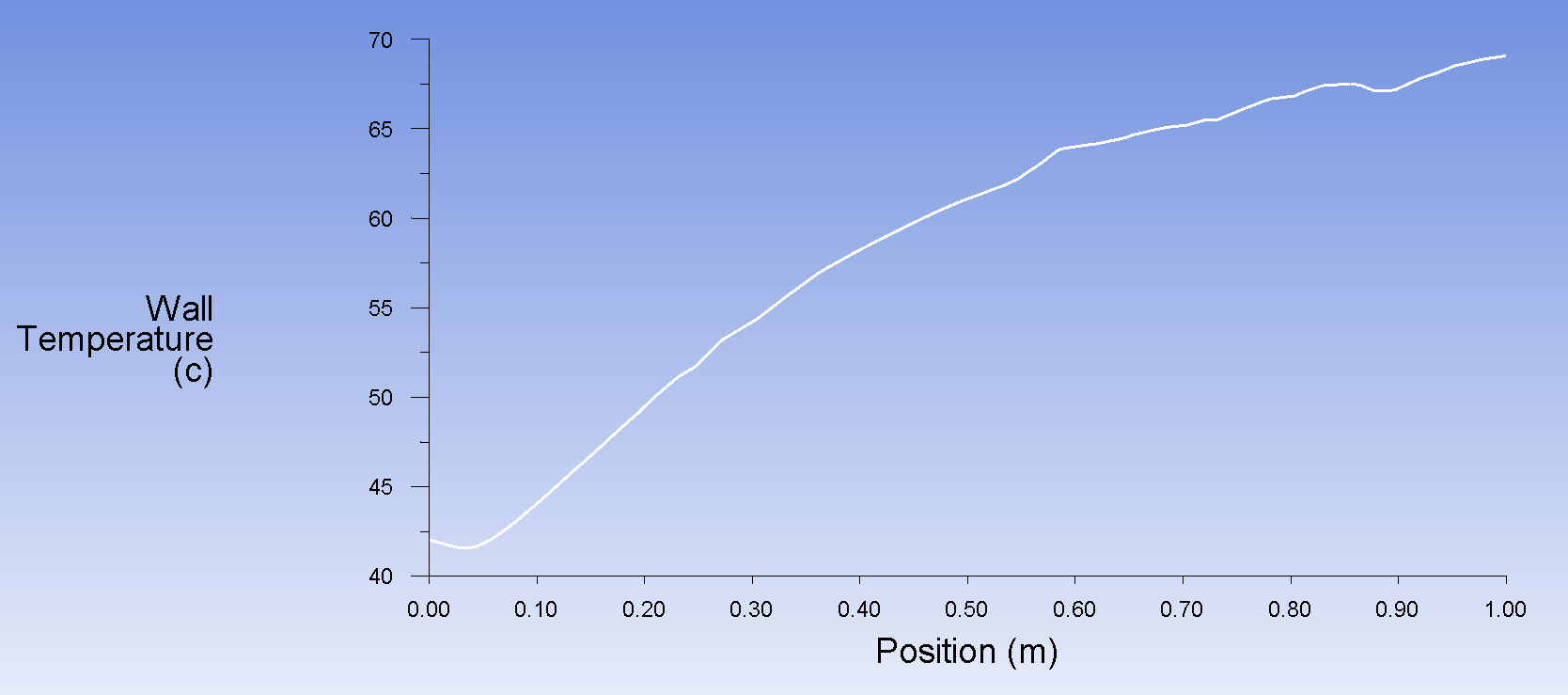
Получаем распределение коэффициента теплоотдачи для поверхности пластины
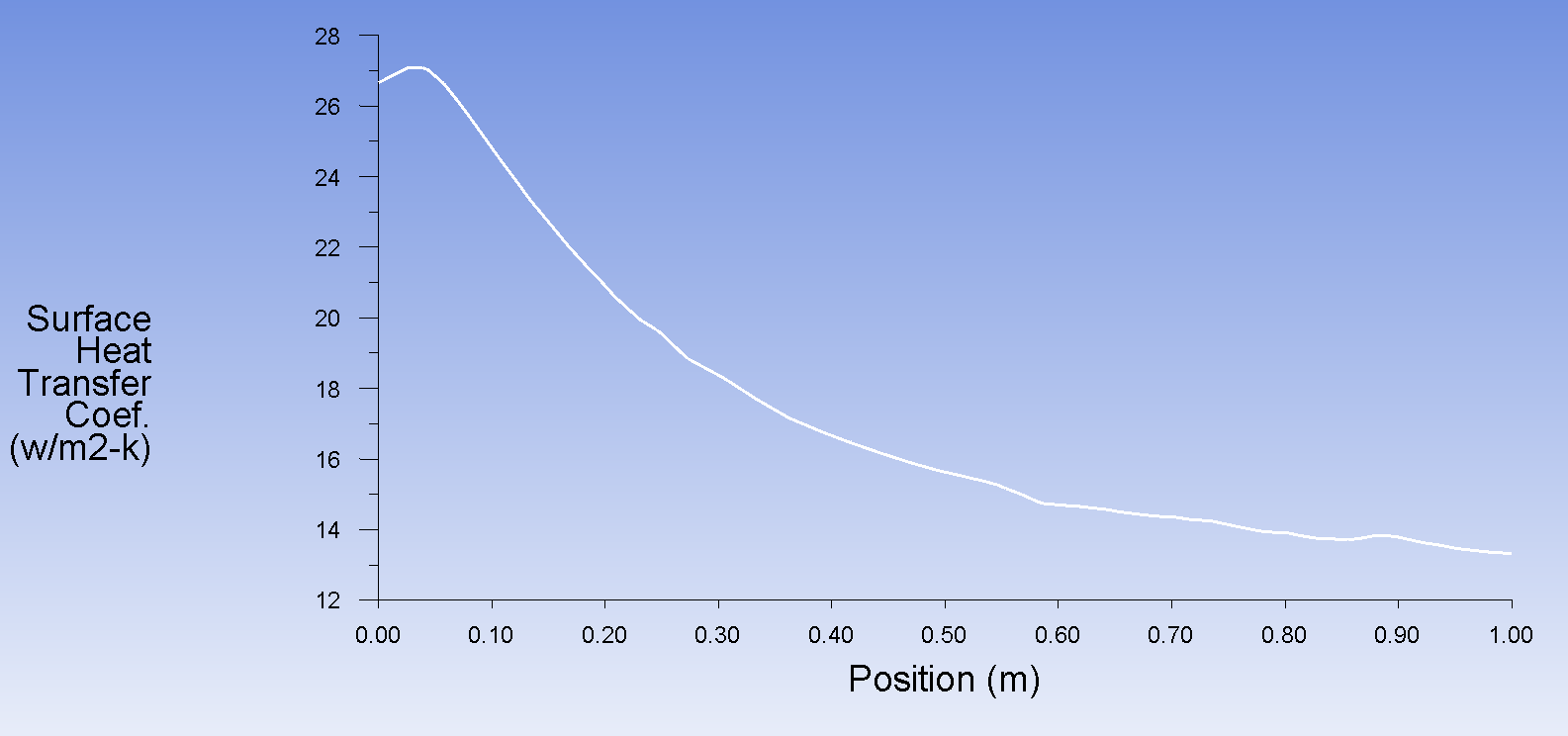
Производим расчет для свободного течения. Получаем распределение температуры для воздушного пространства (греющая пластина расположена слева)
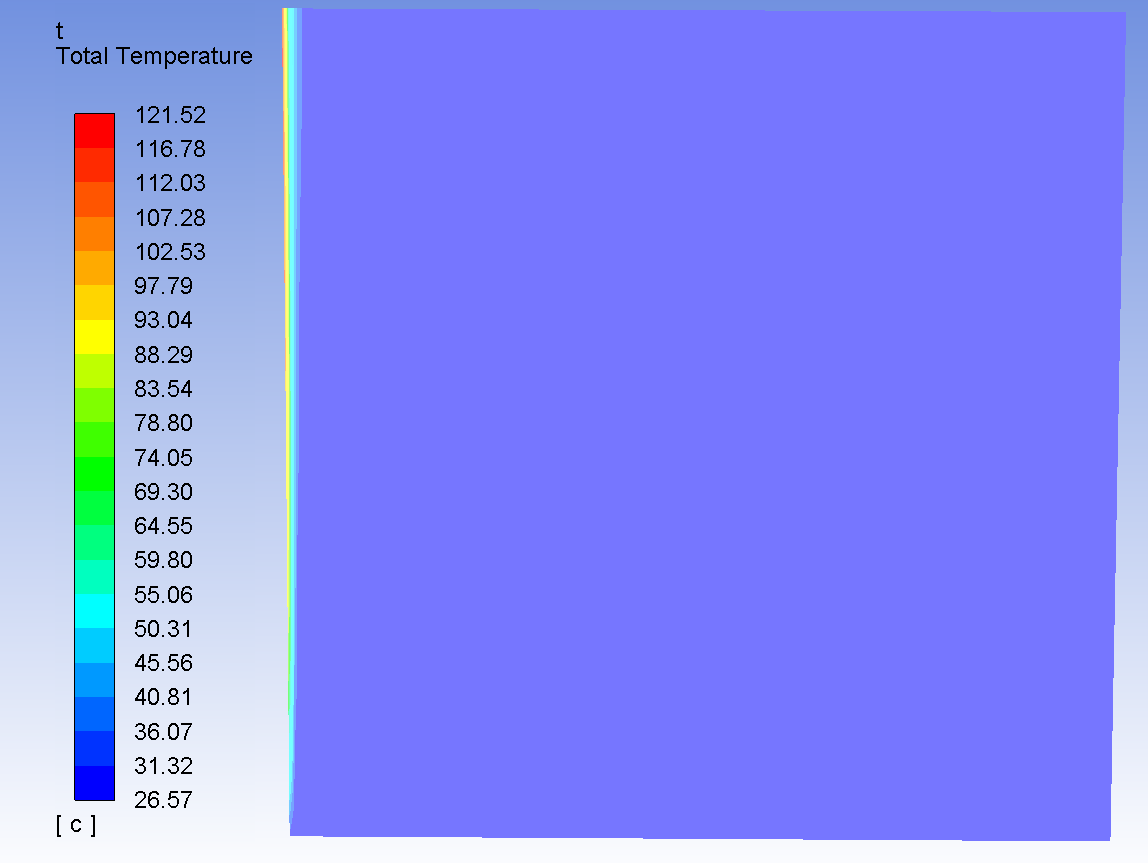
Получаем распределение температуры для поверхности пластины
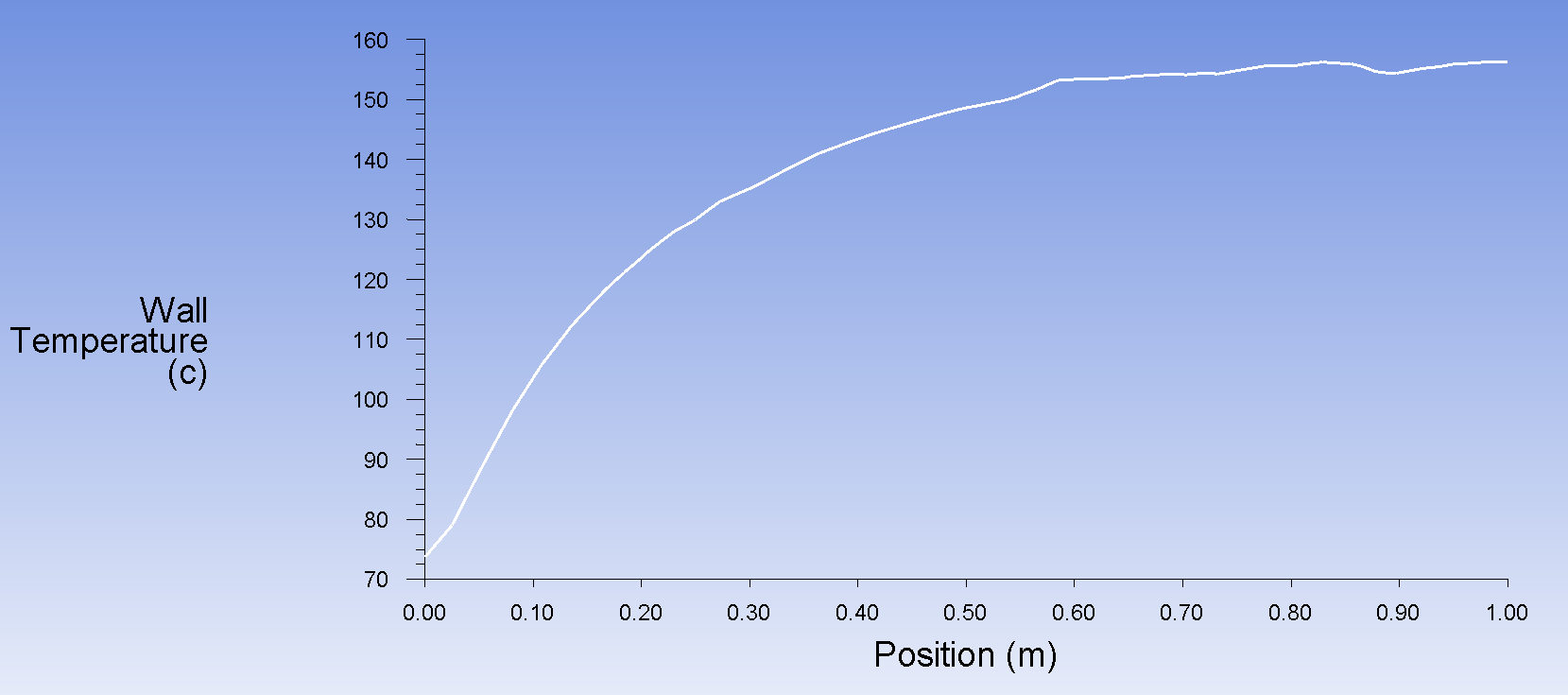
Получаем распределение коэффициента теплоотдачи для поверхности пластины
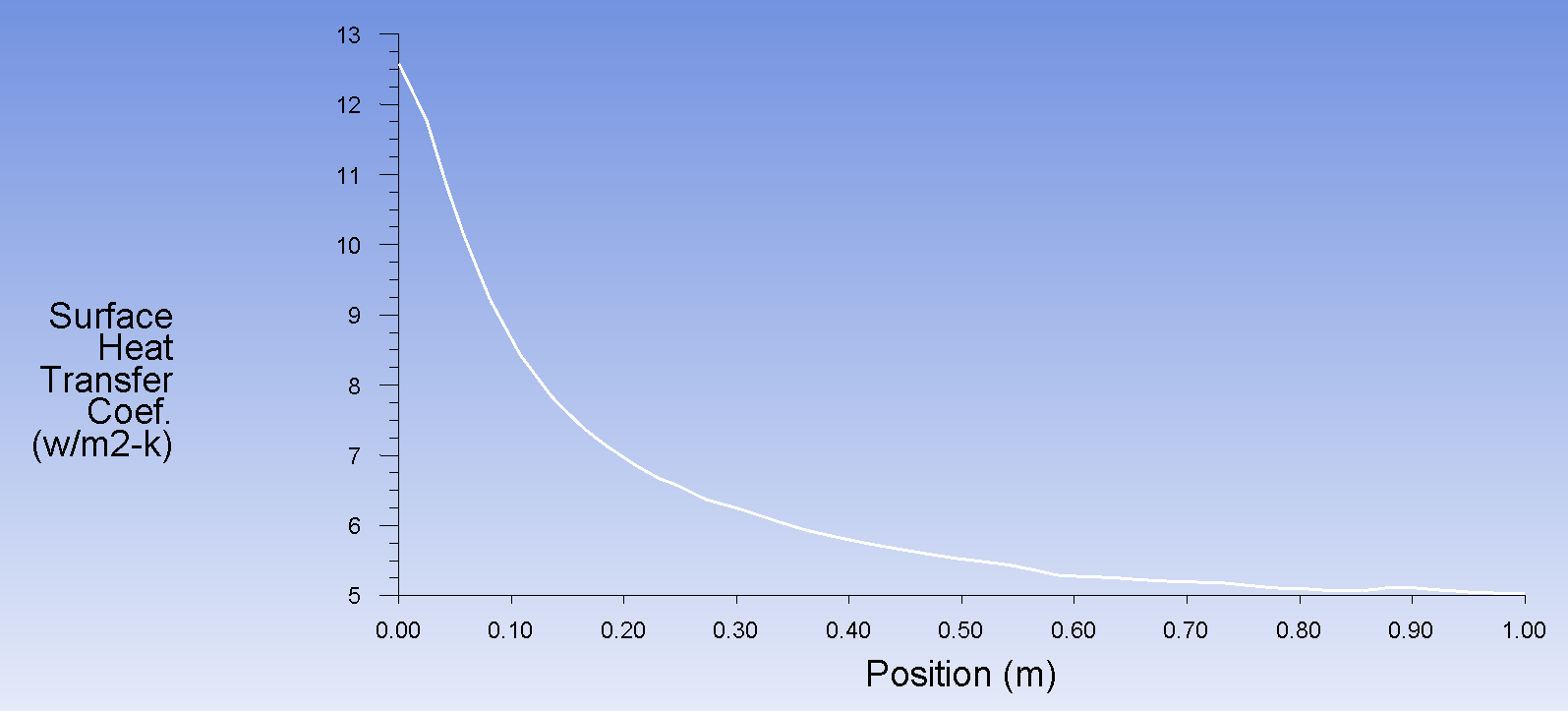
Получаем распределение скоростей для воздушного пространства при свободном движении