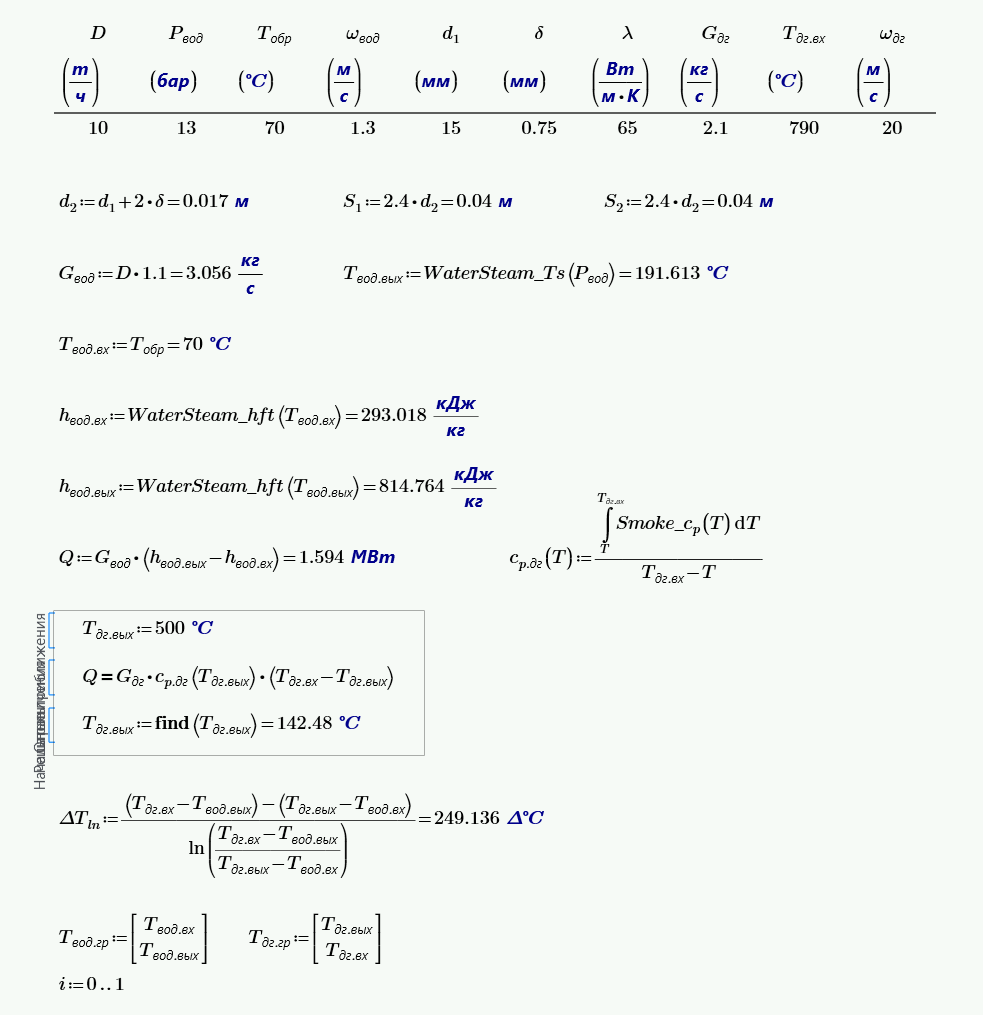
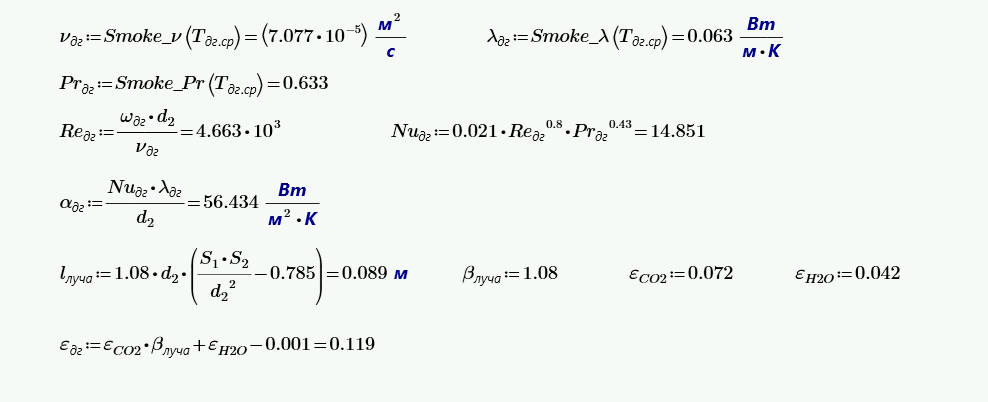Определить: число секций и длину каждой секции змеевикового экономайзера котла ДКВР10-13, а также мощность насоса, необходимую для подачи нагретой воды в топочные экраны и температуру дымовых газов на выходе из экономайзера. Температура воды в обратной линии тепловой сети $t_{обр} = 70$°С.
Скорость воды в трубах экономайзера $\omega_в = 1.3$ м/с, внутренний диаметр трубы экономайзера $d_1 = 15$ мм, толщина стенки трубы экономайзера $d = 0.75$ мм, расход дымовых газов в межтрубном пространстве $G_г = 2.1$ кг/с, температура газов на входе в экономайзер $t_г = 790$ °C, химический состав дымовых газов $СО2 = 13$%, $Н2О = 11$%, относительный продольный шаг трубного пучка экономайзера $S_1$, относительный поперечный шаг трубного пучка экономайзера $S_2$, скорость дымовых газов в узком сечении экономайзера $\omega_г = 20$ м/с. Коэффициент теплопроводности материала экономайзера $\lambda_{эк} = 65$ Вт/м·К. Режим течения - противоток, а также $S_1/d_2=S_2/d_2 = 2.4$.
Решение:
Расход воды в экономайзере, кг/с:
$$G_в = D·1.1·\frac{1000}{3600} = 10·1.1·\frac{1000}{3600} = 3.$$Обратите внимание! Паропроизводительность $D$ определяется по маркировке котла.
Теплота необходимая для нагрева воды, Вт:
$$Q = G_в·c_p·(t_в^{вых} - t_в^{вх}) = 3·4190·(190 - 70) = 1.54·10^6.$$Обратите внимание! Температура воды на выходе из котла $t_в^{вых}$ определяется по давлению насыщения в барабане котла, которое определяется по маркировке котла.
Конечная температура дымовых газов, °C:
$$t_г^{вых} = \frac{G_г·c_г·t_г^{вх} - Q}{G_г·c_г} = \frac{2.1·1350·790 - 1.54·10^6}{2.1·1350} = 205.$$Средне логарифмический температурный напор, °C:
$$\Delta t_{ln} = \frac{(t_г^{вх}-t_в^{вых}) - (t_г^{вых}-t_в^{вх})}{\ln{\left(\frac{t_г^{вх}-t_в^{вых}}{t_г^{вых}-t_в^{вх}}\right)}} = \frac{(790-190) - (205-70)}{\ln{\left(\frac{790-190}{205-70}\right)}} = 312.$$Средняя температура воды, °C:
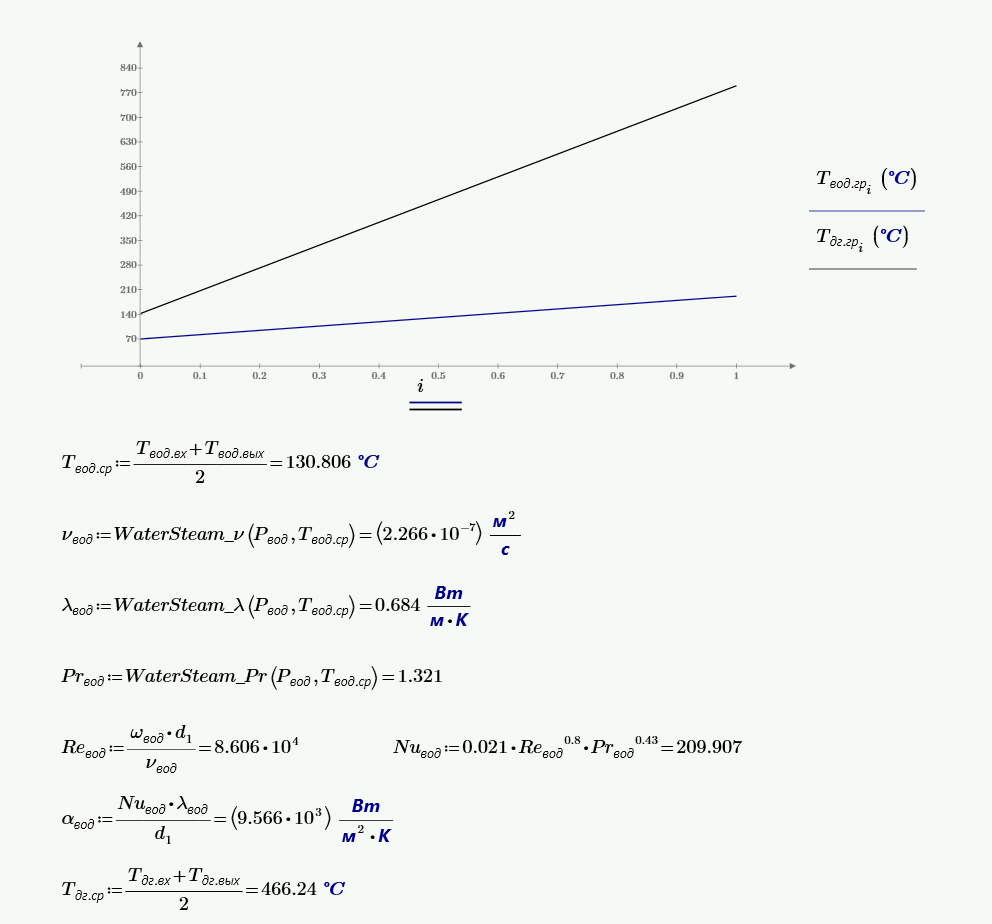
$$t_в = \frac{t_в^{вх}+t_в^{вых}}{2} = \frac{70+190}{2} = 130.$$Свойства воды берем по таблице:
| $t$, °C | $\lambda$, Вт/м·К | $\nu$, м2/с | $Pr$ |
|---|---|---|---|
| $130$ | $0.686$ | $0.233·10^{-6}$ | $1.36$ |
Рассчитываем коэффициент теплоотдачи для воды внутри трубы, при условии его вынужденного движения. Для этого определяем число Рейнольдса при условии равенства температур потока и стенки:
$$Re = \frac{\omega_1·d_1}{\nu_1} = \frac{1.3·0.015}{0.233·10^{-6}} = 8.4·10^4 > 10^4.$$режим течения турбулентный.
Число Нуссельта:
$$Nu = 0.021·Re^{0.8}·Pr^{0.43} = 0.021·(8.4·10^4)^{0.8}·1.36^{0.43} = 207.$$Коэффициент теплоотдачи, Вт/м2·К:
$$\alpha_1 = \frac{Nu·\lambda}{d_1} = \frac{207·0.686}{0.0165} = 9500.$$Рассчитываем коэффициент теплоотдачи для дымовых газов в пучке труб, при условии их вынужденного движения.
Средняя температура дымовых газов, °C:
$$t_г = \frac{t_г^{вх}+t_г^{вых}}{2} = \frac{790+205}{2} = 498.$$Свойства дымовых газов берем по таблице:
| $t$, °C | $\lambda$, Вт/м·К | $\nu$, м2/с | $Pr$ |
|---|---|---|---|
| $498$ | $0.0656$ | $76.30·10^{-6}$ | $0.63$ |
Внешний диаметр труб, м:
$$d_2 = d_1 + 2·\delta = 0.015 + 2·0.00075 = 0.0165.$$Определяем число Рейнольдса:
$$Re = \frac{\omega_2·d_2}{\nu_2} = \frac{20·0.0165}{76.3·10^{-6}} = 4325.$$Число Нуссельта для шахматного расположения:
$$Nu = 0.41·Re^{0.8}·Pr^{0.33}·\left(\frac{S_1}{S_2}\right)^{\frac{1}{6}} = 0.41·4325^{0.8}·0.63^{0.33}·\left(1\right)^{\frac{1}{6}} = 53.$$Коэффициент теплоотдачи конвективный, Вт/м2·К:
$$\alpha_{2к} = \frac{Nu·\lambda}{d_2} = \frac{53·0.0656}{0.0165} = 265.$$Средняя длина пути луча, м:
$$l = 1.08·d_2·\left(\frac{S_1·S_2}{d_2^2}-0.785\right) = 1.08·0.0165·\left(2.4^2-0.785\right) = 0.08.$$По графикам находим степени черноты углекислого газа и воды. Тогда степень черноты дымовых газов:
$$\varepsilon_г = \varepsilon_{CO2}+\beta·\varepsilon_{H20} - \Delta \varepsilon_г = 0.072+1.08·0.042 - 0.001 = 0.117.$$Обратите внимание! Графики можно посмотреть здесь.
Лучистый тепловой поток по закону Стефана-Больцмана принимая температуру стенки $t_c = 270$ °С, Вт/м2:
$$q = 5.685·\varepsilon_г·\left(\left(\frac{t_г+273}{100}\right)^4 - \left(\frac{t_{ст}+273}{100}\right)^4\right) = 5.685·0.117·\left(\left(\frac{498+273}{100}\right)^4 - \left(\frac{270+273}{100}\right)^4\right) = 1860.$$Коэффициент теплоотдачи лучистый, Вт/м2·К:
$$\alpha_{2л} = \frac{q}{t_г - t_{ст}} = \frac{1860}{498 - 270} = 8.2.$$Коэффициент теплоотдачи дымовых газов, Вт/м2·К:
$$\alpha_2 = \alpha_{2к} + \alpha_{2л} = 265 + 8.2 = 273.$$Коэффициент теплопередачи, Вт/м·К:
$$k = \frac{\pi}{\frac{1}{\alpha_1·d_1}+\frac{1}{2·\lambda_{эк}}·\left(\frac{d_2}{d_1}\right)+\frac{1}{\alpha_2·d_2}} = \frac{\pi}{\frac{1}{9500·0.015}+\frac{1}{2·45}·\left(\frac{0.0165}{0.015}\right)+\frac{1}{273·0.0165}} = 10.4.$$Длина всех труб экономайзера, м:
$$L = \frac{Q}{k·\Delta t_{ln}} = \frac{1.54·10^6}{10.4·312} = 474.$$Проверяем температуру стенки с внутренней стороны по уравнению Ньютона-Рихмана, °C:
$$t_{c1} = t_1 + \frac{Q}{\alpha_1·\pi·d_1·L} = 130 + \frac{1.54·10^6}{9500·\pi·0.015·474} = 137.$$Проверяем температуру стенки с внешней стороны по уравнению Ньютона-Рихмана, °C:
$$t_{c2} = t_2 - \frac{Q}{\alpha_2·\pi·d_2·L} = 130 - \frac{1.54·10^6}{273·\pi·0.0165·474} = 269.$$Количество труб теплообменника, шт:
$$n = \frac{4·G_в}{\rho·\pi·d_1^2·\omega_1} = \frac{4·3}{1000·\pi·0.015^2·1.3} = 14.$$Длина каждой трубы, м:
$$L_{тр} = \frac{L}{n} = \frac{474}{14} = 34.$$Расчет гидравлических сопротивлений. Сопротивление трения, Па:
$$\Delta p_л = \xi·\frac{L}{d_1}·\frac{\rho·\omega^2}{2} = 0.019·\frac{474}{0.015}·\frac{1000·1.3^2}{2} = 5·10^5.$$ $$\xi = \frac{1}{\left(1.82·lg(Re)-1.64\right)^2} = \frac{1}{\left(1.82·lg(8.4·10^4)-1.64\right)^2} = 0.019.$$Местные сопротивления при условии ширины экономайзера не более 3 м, Па:
$$\Delta p_м = \zeta·\frac{\rho·\omega^2}{2} = (2·1.2·14·11)·\frac{1000·1.3^2}{2} = 3.1·10^5.$$Сумма сопротивлений, Па:
$$\Delta p = \Delta p_л + \Delta p_м = 5·10^5 + 3.1·10^5 = 8.1·10^5.$$Мощность насоса, Вт:
$$N = \frac{\Delta p·G_в}{\rho·\eta} = \frac{8.1·10^5·3}{1000·0.75} = 3300.$$