Пластина толщиной $\delta = 60$ мм и коэффициентом теплопроводности $\lambda = 65$ Вт/м·К с равномерно распределенными внутренними источниками теплоты $q_v = 10^6$ Вт/м3 охлаждается с обеих сторон. С одной стороны на пластину наложена изоляция толщиной $\delta_{из} = 4$ мм и коэффициентом теплопроводности $\lambda_{из} = 12$ Вт/м·К . Температура охлаждающей жидкости $t_ж = 150$ °C и коэффициент теплоотдачи $\alpha = 10^4$ Вт/м2·К. Условия с неизолированной стороны - теплоотдача
Определить максимальную температуру, температуры в центре, на поверхностях пластины и изоляции.
Для упрощения задачи путем учета изоляции в качестве дополнительного термического сопротивления теплоотдачи, рассчитаем приведенный коэффициент теплоотдачи, Вт/м2·К:
$$\alpha_{пр} = \frac{1}{\frac{1}{\alpha}+\frac{\delta_{из}}{\lambda_{из}}} = \frac{1}{\frac{1}{10^4}+\frac{0.004}{12}} = 2300.$$При указанных условиях температура пластины будет изменяться только вдоль оси x, тогда дифференциальное уравнение принимает вид:
$$\frac{\partial^2t}{\partial x^2}+\frac{q_v}{\lambda} = 0.$$После интегрирования получим:
$$\frac{\partial t}{\partial x} = -\frac{q_v·x}{\lambda} + C_1;$$ $$t = -\frac{q_v·x^2}{2·\lambda}+C_1·x+C_2.$$Постоянные интегрирования определяются из граничных условий.
при $x = 0$
$$\lambda·\frac{\partial t}{\partial x} = \alpha·(t-t_ж).$$при $x = \delta$
$$-\lambda·\frac{\partial t}{\partial x} = \alpha_{пр}·(t-t_ж).$$Обратите внимание! Вид уравнений зависит от условий на поверхности тела.
Тогда:
$$\lambda·\left(-\frac{q_v·0}{\lambda}+C_1\right)=\alpha·\left(\left(-\frac{q_v·0^2}{2·\lambda}+C_1·0+C_2\right)-t_ж\right);$$ $$-\lambda·\left(-\frac{q_v·\delta}{\lambda}+C_1\right)=\alpha_{пр}·\left(\left(-\frac{q_v·\delta^2}{2·\lambda}+C_1·\delta+C_2\right)-t_ж\right).$$Или
$$65·\left(-\frac{10^6·0}{65}+C_1\right)=10^4·\left(\left(-\frac{10^6·0^2}{2·65}+C_1·0+C_2\right)-150\right);$$ $$-65·\left(-\frac{10^6·0.06}{65}+C_1\right)=2300·\left(\left(-\frac{10^6·0.06^2}{2·65}+C_1·0.06+C_2\right)-150\right).$$Решая систему находим: $C_1 = 567.2$, $C_2 = 154$.
Задаем распределение температуры внутри пластины:
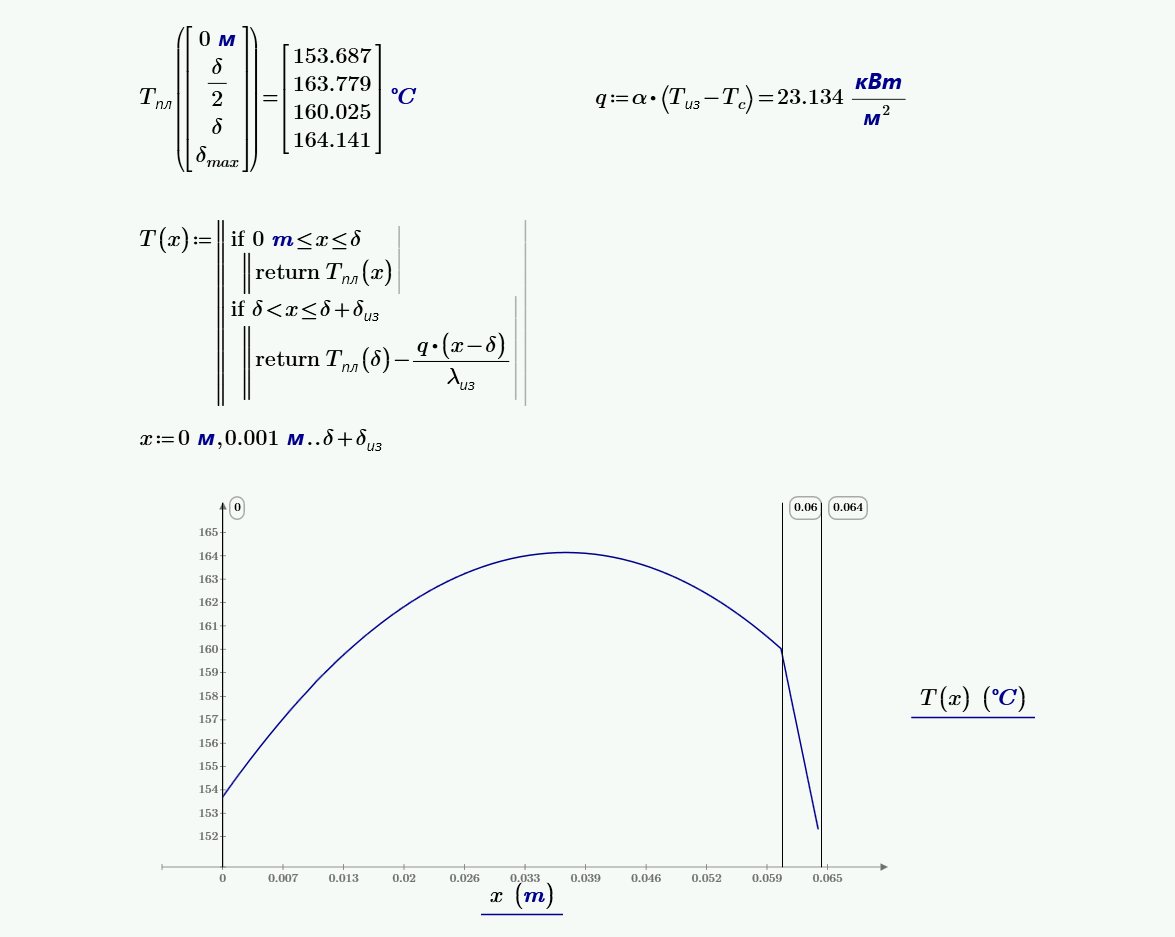
$$t(x) = -\frac{q_v·x^2}{2·\lambda}+C_1·x+C_2= -\frac{10^6·x^2}{2·65}+567.2·x+154.$$Находим температуры в середине и на краях пластины:
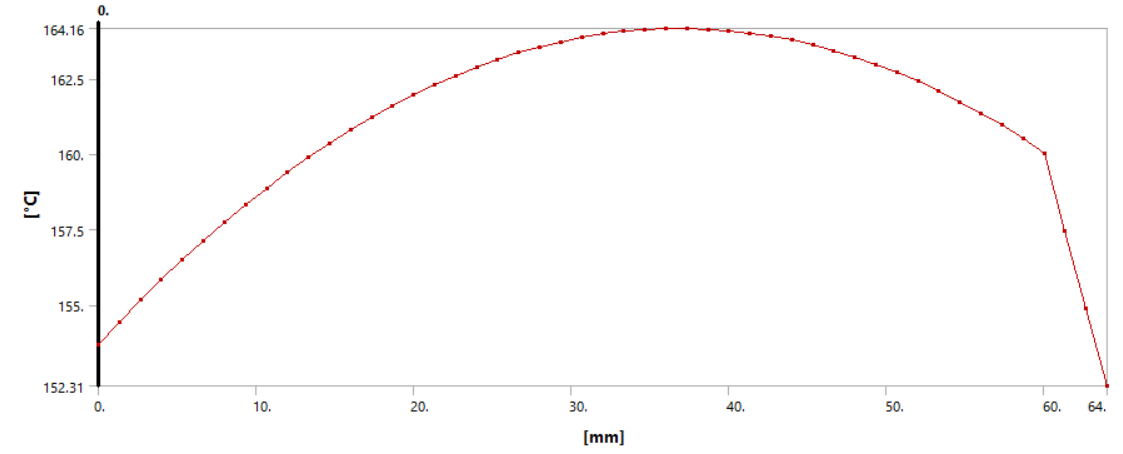
при $x = 0$ м температура равна $t(0) = 153$ °C;
при $x = \delta/2 = 0.03$ м температура равна $t(0.03) = 164$ °C;
при $x = \delta = 0.06$ м температура равна $t(0.06) = 160$ °C.
Находим максимальную температуру используя свойства экстремумом:
при $\partial t/\partial x = 0$ или $0 = -10^6·x_{max}/65+567.2$ находим $x_{max} = 0.037$ м;
при $x = x_{max} = 0.037$ м температура равна $t_{max}(0.037) = 164.1$ °C.
Находим температуру поверхности изоляции:
$$\frac{\lambda_{из}}{\delta_{из}}·(t(\delta)-t_{из})=\alpha·(t_{из}-t_ж);$$ $$\frac{12}{0.004}·(164-t_{из})=10^4·(t_{из}-150).$$Откуда температура изоляции равна $t_{из} = 152$ °С.

Создаем модель
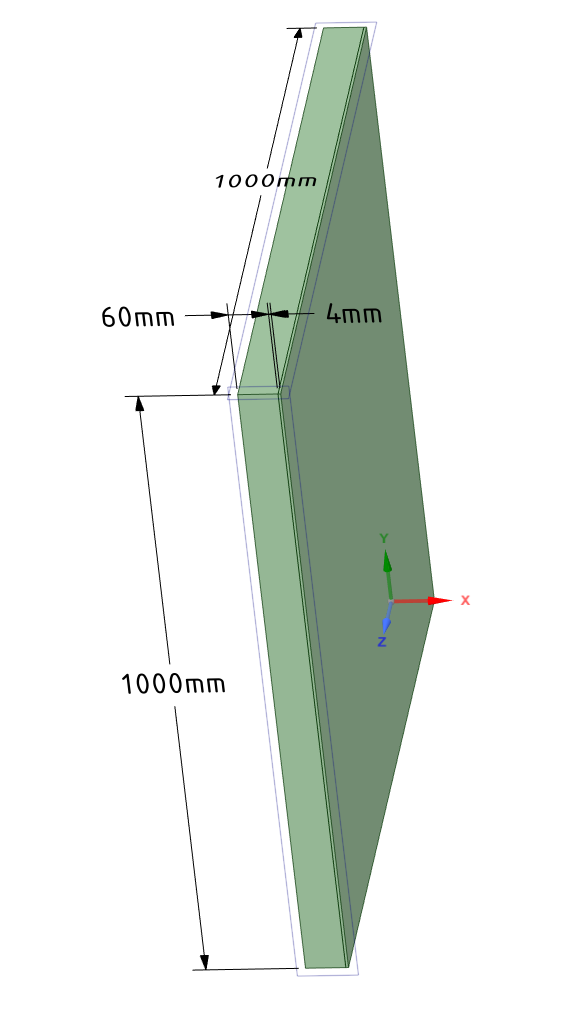
Создаем сетку
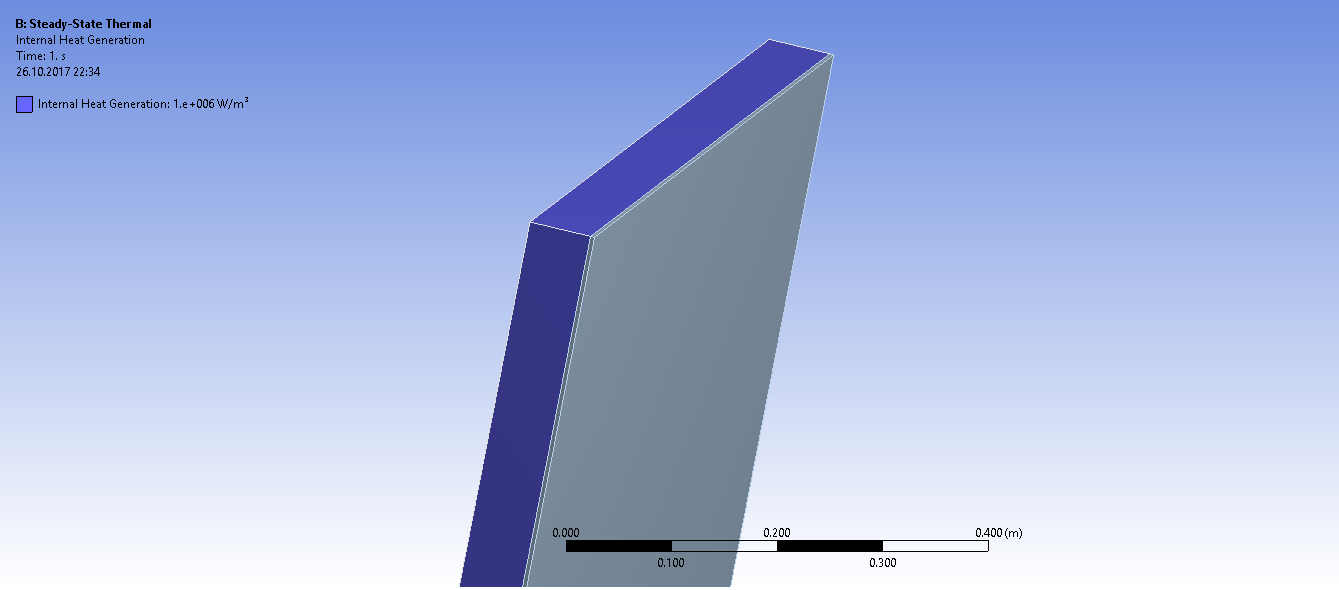
Задаем внутренние источники тепла
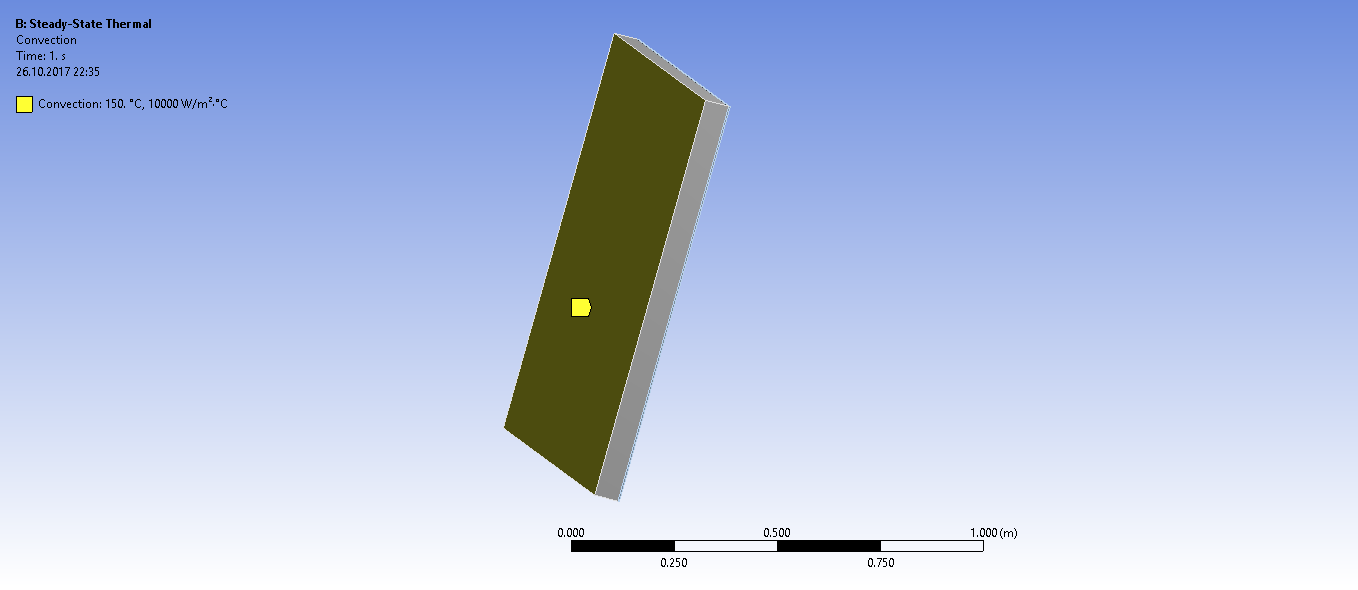
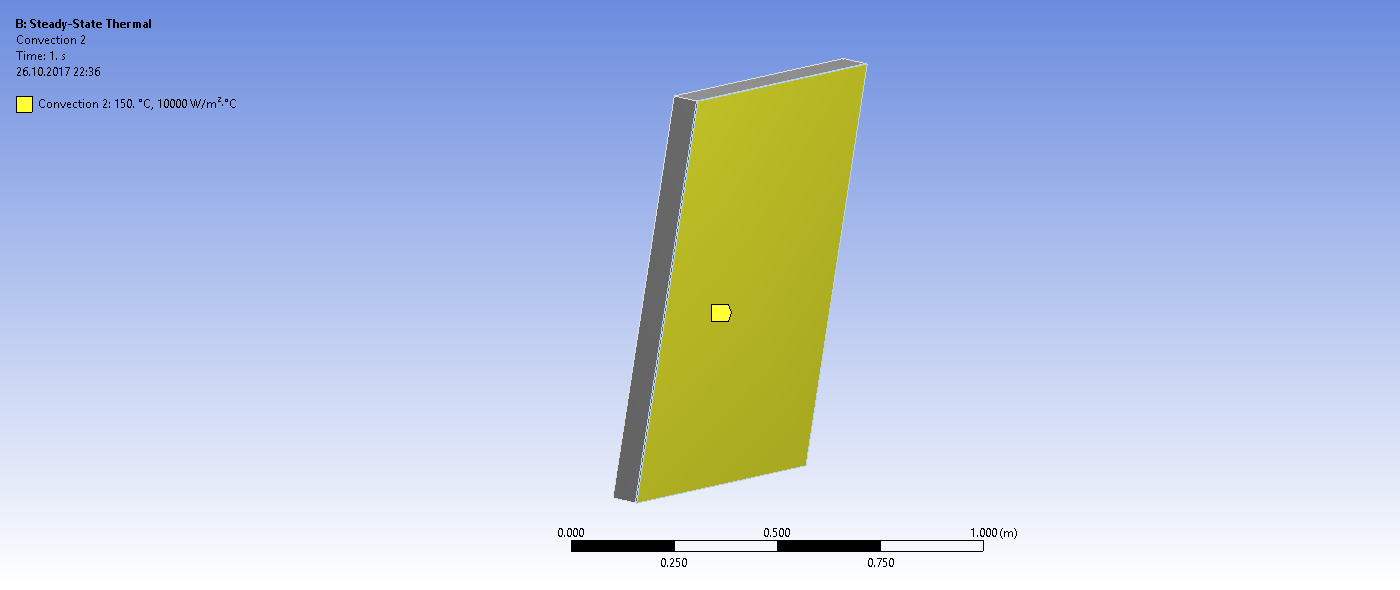
Задаем граничные условия конвективного теплообмена с обоих сторон
Получаем распределение температур